R で tukey テストを実行する方法

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

ANOVA 表全体のp 値が一定の有意性レベルを下回っている場合、グループ平均の少なくとも 1 つが他の平均とは異なると言える十分な証拠があります。

ただし、これではどのグループが互いに異なるかはわかりません。これは単に、すべてのグループの平均が等しいわけではないことを示しています。どのグループが互いに異なっているかを正確に知るには、 事後テストを実行する必要があります。

最も一般的に使用される事後テストの 1 つはTukey テストです。これを使用すると、 家族ごとの誤り率を制御しながら、各グループの平均値間のペアごとの比較を実行できます。

このチュートリアルでは、R で Tukey テストを実行する方法について説明します。

注:研究内のグループのいずれかが対照グループとみなされる場合は、代わりに事後テストとしてダネットのテストを使用する必要があります。

例: R での Tukey テスト

ステップ 1: ANOVA モデルを当てはめます。

次のコードは、3 つのグループ (A、B、および C) を含む偽のデータ セットを作成し、一元配置分散分析モデルをデータに適合させて、各グループの平均値が等しいかどうかを判断する方法を示しています。

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA 表からの全体的な p 値は7.55e-11であることがわかります。この数値は 0.05 未満であるため、各グループの平均値が等しくないと言える十分な証拠があります。したがって、Tukey 検定を実行して、どのグループの平均値が異なるかを正確に判断できます。

ステップ 2: Tukey テストを実行します。

次のコードは、 TukeyHSD()関数を使用して Tukey テストを実行する方法を示しています。

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

p 値は、各プログラム間に統計的に有意な差があるかどうかを示します。結果は、各プログラムの平均体重減少の間に 0.05 有意水準で統計的に有意な差があることを示しています。

特に：

• B と A の平均の差の P 値: 0.0100545
• C と A の平均の差の P 値: 0.0000000
• C と B の平均の差の P 値: 0.0000199

ステップ 3: 結果を視覚化します。

また、 plot(TukeyHSD())関数を使用して信頼区間を視覚化することもできます。

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

注: las引数は、目盛ラベルが軸に対して垂直 (las=2) である必要があることを指定します。

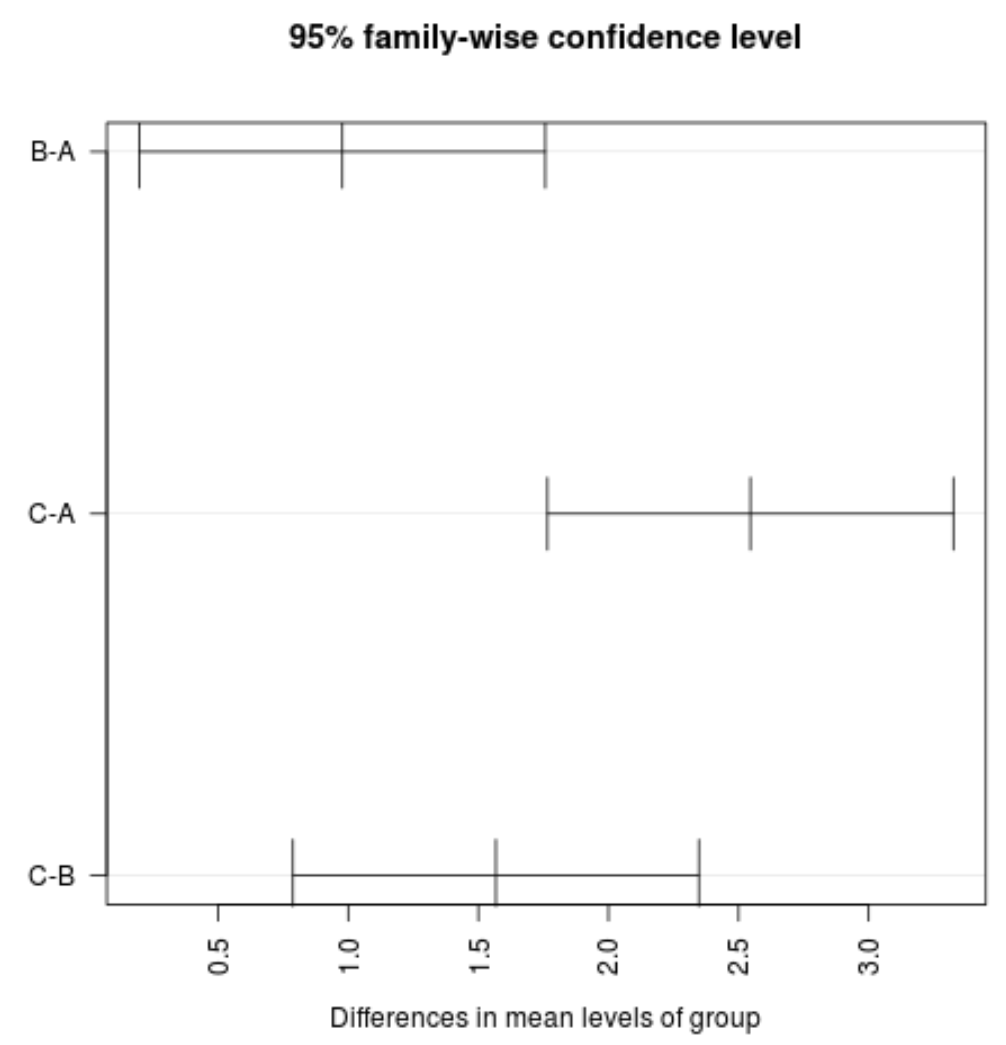
グループ間の平均値の信頼区間には値 0 が含まれていないことがわかります。これは、3 つのグループ間の平均損失に統計的に有意な差があることを示しています。これは、仮説検定のすべての p 値が 0.05 未満であることと一致しています。

この特定の例では、次のように結論付けることができます。

• グループ C の平均値は、グループ A およびグループ B の平均値よりも大幅に高くなっています。
• グループBの平均値はグループAの平均値よりも大幅に高くなっています。

追加リソース

ANOVA で事後テストを使用するためのガイド
R で一元配置分散分析を実行する方法
R で二元配置分散分析を実行する方法