機械学習におけるバイアスと分散のトレードオフとは何ですか?

データセットに対するモデルのパフォーマンスを評価するには、モデルの予測が観察されたデータとどの程度一致するかを測定する必要があります。

回帰モデルの場合、最も一般的に使用される指標は平均二乗誤差 (MSE) で、次のように計算されます。

MSE = (1/n)*Σ(y _i – f(x _i )) ²

金：

• n:観測値の総数
• y _i : ^{i 番目}の観測値の応答値
• f( _xi ): i^番目の観測値の予測応答値

モデルの予測が観測値に近づくほど、MSE は低くなります。

ただし、私たちが気にするのはMSE テスト、つまりモデルが目に見えないデータに適用されるときの MSE だけです。これは、既存のデータではなく、未知のデータに対してモデルがどのように実行されるかのみを考慮しているためです。

たとえば、株価を予測するモデルの履歴データの MSE が低いのは問題ありませんが、実際には、そのモデルを使用して将来のデータを正確に予測できるようにしたいと考えています。

MSE テストは依然として 2 つの部分に分割できることがわかりました。

(1) 分散:別のトレーニング セットを使用して関数f を推定した場合に変化する量を指します。

(2) バイアス:非常に複雑な実際の問題に、より単純なモデルを使用してアプローチすることによって生じる誤差を指します。

数学用語で書くと次のようになります。

MSE テスト = Var( f̂( x ₀ )) + [バイアス( f̂( x ₀ ))] ² + Var(ε)

MSE テスト = 分散 + バイアス² + 既約誤差

3 番目の項である既約誤差は、説明変数のセットと応答変数の間の関係に常にノイズが存在するため、どのモデルでも削減できない誤差です。

高いバイアスを持つモデルは、分散が小さい傾向があります。たとえば、線形回帰モデルは、バイアスが高く (説明変数と応答変数の間に単純な線形関係があると仮定)、分散が低い (モデルの推定値はサンプル間であまり変化しない) 傾向があります。もう一方）。

ただし、バイアスが低いモデルは分散が高くなる傾向があります。たとえば、複雑な非線形モデルは、バイアスが低く (説明変数と応答変数の間に特定の関係を仮定しない)、分散が大きくなる傾向があります (モデルの推定値は、学習のサンプルから別のサンプルに大きく変化する可能性があります)。

バイアスと分散のトレードオフ

バイアスと分散のトレードオフは、バイアスを減らすことを選択した場合（一般に分散が増加する）、または分散を減少することを選択した場合（一般にバイアスが増加する）に発生するトレードオフを指します。

次のグラフは、このトレードオフを視覚化する方法を示しています。

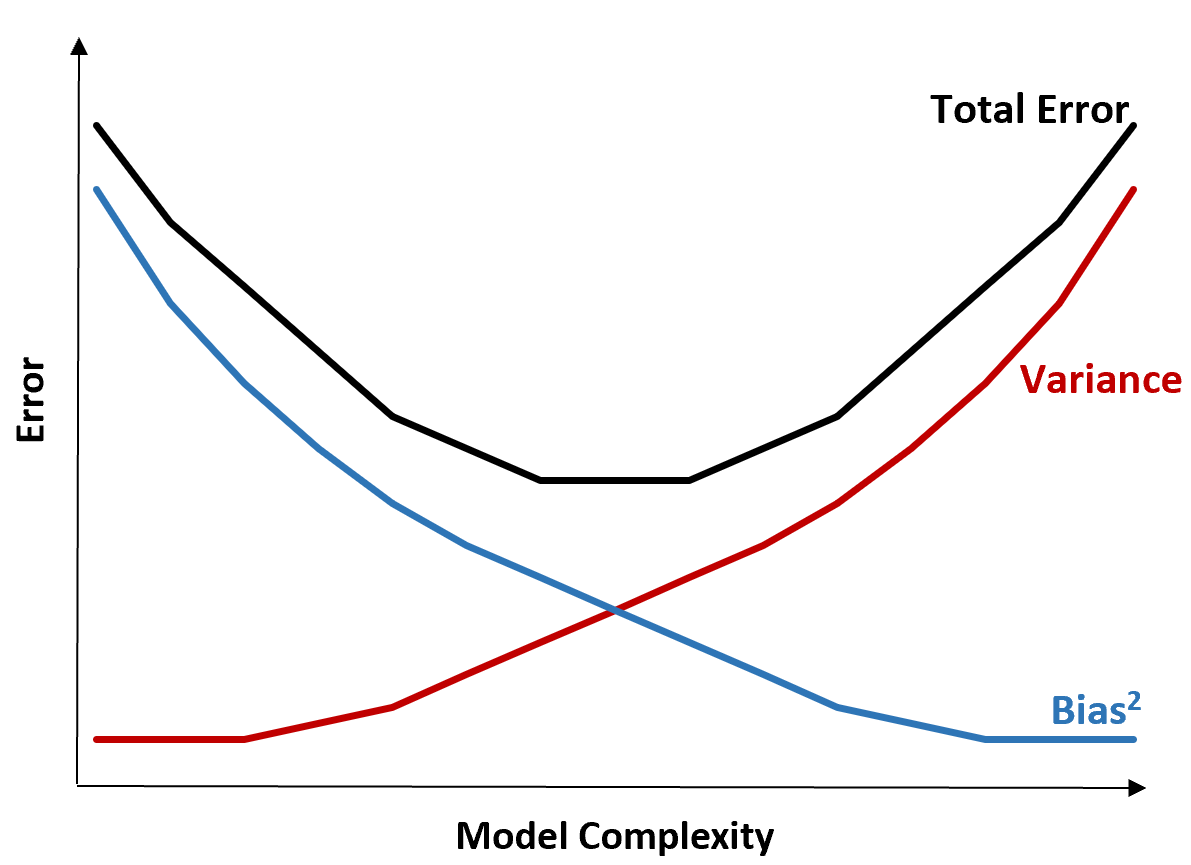
モデルの複雑さが増すにつれて合計誤差は減少しますが、それはある時点までに限られます。特定の点を超えると、分散が増加し始め、合計誤差も増加し始めます。

実際には、モデルの合計誤差を最小化することのみを考慮し、必ずしも分散や偏りを最小化する必要はありません。合計誤差を最小限に抑える方法は、分散と偏りの間の適切なバランスを見つけることであることがわかりました。

言い換えれば、説明変数と応答変数の間の真の関係を捉えるのに十分な複雑さのモデルが必要ですが、実際には存在しないパターンを検出できるほど複雑すぎないモデルが必要です。

モデルが複雑すぎると、データが過剰適合してしまいます。これは、トレーニング データ内で単に偶然に発生したパターンを見つけるのが非常に難しいために発生します。このタイプのモデルは、非表示のデータではパフォーマンスが低下する可能性があります。

しかし、モデルが単純すぎると、データが過小評価されてしまいます。これは、説明変数と応答変数の間の真の関係が実際よりも単純であると想定されているために発生します。

機械学習で最適なモデルを選択する方法は、バイアスと分散のバランスを見つけて、将来の目に見えないデータでモデルをテストする際のエラーを最小限に抑えることです。

実際には、テストの MSE を最小限に抑える最も一般的な方法は、相互検証を使用することです。