Bartlett の分散均一性検定 (定義と例)
バートレット検定は、複数のグループ間の分散が等しいかどうかを判断するために使用される統計検定です。
多くの統計検定 (一元配置 ANOVAなど) は、サンプル間の分散が等しいことを前提としています。バートレット検定を使用して、この仮説を検証できます。
次の手順では、バートレット テストの実行方法を説明します。
注:この検定を、観測された相関行列と単位行列を比較するために使用されるBartlett の球面度検定と混同しないでください。
バートレット テストを実行する手順
Bartlett 検定では、次の帰無仮説と対立仮説を使用します。
H 0 :各グループ間の分散は等しい。
H A :少なくとも 1 つのグループには、他のグループと等しくない分散があります。
検定統計量は次のように計算できます。
B = (nk)lns 2 – Σ(n j -1)lns j 2 / c
金:
- n: すべてのグループの観測値の合計数
- k: グループの総数
- ln: 「自然対数」を意味します。
- s 2 : プールされた分散
- n j : グループ j 内の観測値の数
- s j 2 : グループ j の分散
そして、それは次のように計算されます。
- c = 1 + (1/3(k-1))*(Σ(1/(n j -1)) – (1/(nk))
この検定統計量は、k-1 自由度のカイ二乗分布に従います。つまり、B~X 2 (k-1)です。
検定統計量に対応するp 値が特定の有意水準 (α = 0.05 など) を下回っている場合、帰無仮説は棄却され、すべてのグループの分散が同じではないと結論付けることができます。
例: バートレット テスト
教授が、3 つの異なる勉強法が試験の平均点の違いにつながるかどうかを知りたいと考えているとします。
彼女は 10 人の学生をランダムに割り当て、1 週間各テクニックを使用させ、各学生に同じ難易度の試験を課します。
30 名の学生の試験結果は次のとおりです。

教授は、一元配置分散分析を実行して、3 つの手法が試験の異なる平均点につながるかどうかを確認したいと考えていますが、最初にバートレット検定を実行して、3 つのグループの分散が等しいことを確認する必要があります。
バートレット テストを手動で実行するのは面倒なので、次のデータ値をバートレット テスト計算機に入力します。
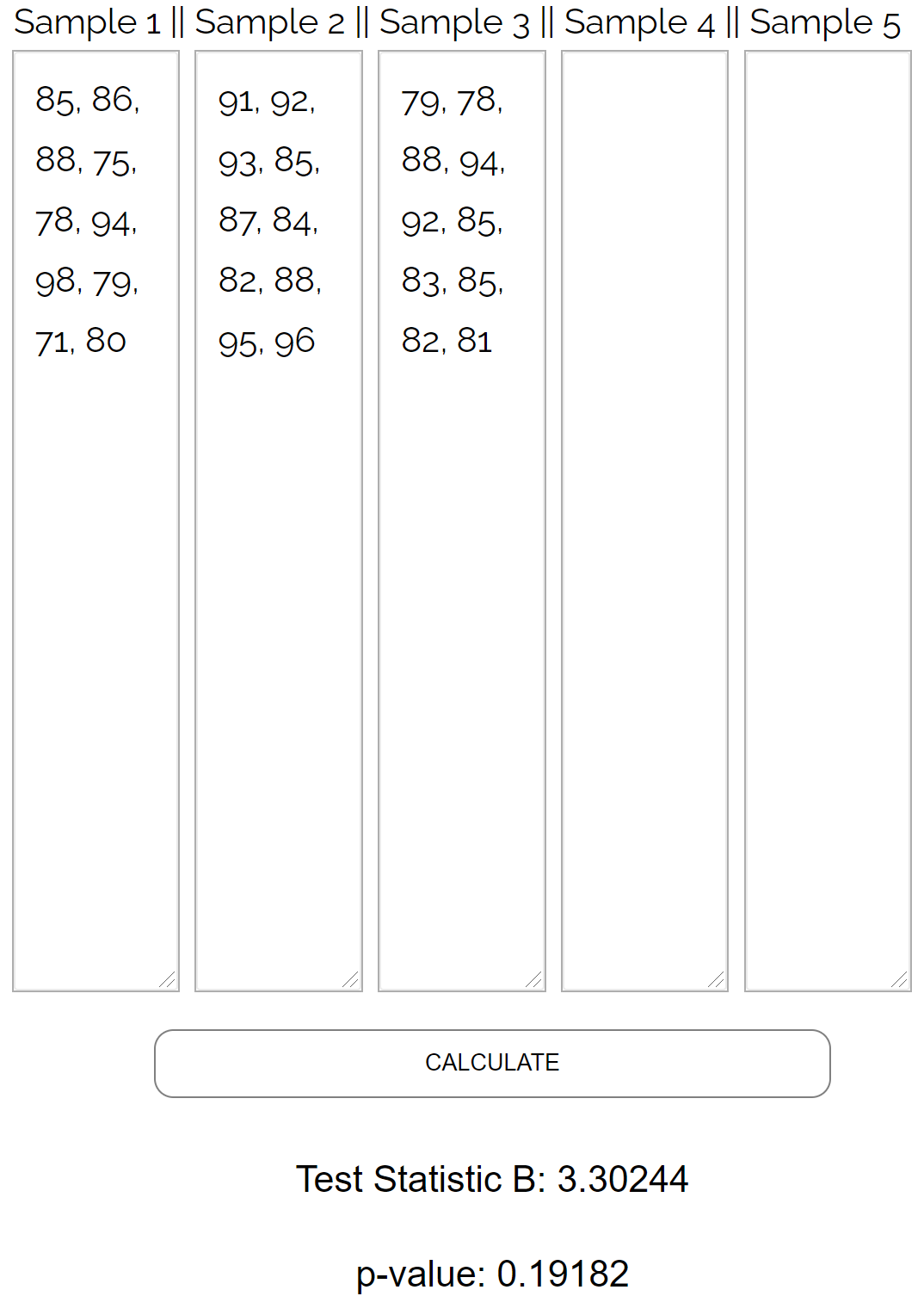
テストは次の結果を返します。
- 検定統計量B : 3.30244
- P 値: 0.19182
p 値は 0.05 未満ではないため、教授は帰無仮説を棄却できません。言い換えれば、彼女は 3 つのグループに異なるギャップがあると言える十分な証拠を持っていません。
したがって、一元配置分散分析の実行を続行できます。
追加リソース
R で Bartlett テストを実行する方法 (ステップバイステップ)
Python で Bartlett テストを実行する方法 (ステップバイステップ)