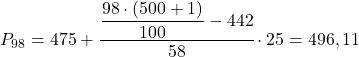パーセンタイル (統計)

この記事では、パーセンタイルとは何か、およびその計算方法について説明します。解決済みのパーセンタイル演習があり、さらに、オンライン計算機を使用してデータ サンプルの任意のパーセンタイルを計算できます。

パーセンタイルとは何ですか?

統計において、パーセンタイルは、順序付けされたデータのセットを 100 等分に分割する値です。したがって、パーセンタイルは、データセットのパーセンテージが下回る値を示します。

たとえば、35 パーセンタイル値は、観測データの 35% よりも高くなりますが、残りのデータよりは低くなります。

パーセンタイルは大文字 P とパーセンタイル インデックスで表されます。つまり、1 番目のパーセンタイルは P ₁ 、40 番目のパーセンタイルは P ₄₀ 、79 番目のパーセンタイルは P ₇₉などとなります。

👉以下の計算機を使用して、任意のデータセットのパーセンタイルを計算できます。

同様に、パーセンタイルは、四分位、五分位、十分位と同様に、中心以外の位置の尺度です。これらの分位タイプのそれぞれの意味は、当社の Web サイトで確認できます。

赤ちゃんが正しく成長しているかどうかを判断するのに役立つ、記録された値を含む成長表があるため、パーセンタイルという用語は、赤ちゃんの体重と身長を他の赤ちゃんの標準値と比較するためにも使用されることに注意してください。 。 。

パーセンタイルの計算方法

統計データ系列のパーセンタイルの位置を計算するには、パーセンタイル数にデータ ポイントの総数に 1 を加えた合計を乗算し、その結果を 100 で割る必要があります。

したがって、パーセンタイルの式は次のようになります。

注意:この式はパーセンタイルの位置を示しますが、その値は示しません。パーセンタイルは、式で求めた位置にあるデータとなります。

ただし、この式の結果が 10 進数になる場合があるため、結果が 10 進数であるかどうかに応じて 2 つのケースを区別する必要があります。

• 数式の結果が小数部を除いた数値である場合、パーセンタイルは上記の数式で指定された位置にあるデータに対応します。
• 式の結果が小数部を含む数値の場合、正確なパーセンタイル値は次の式を使用して計算されます。

ここで、x _iおよびx _i+1は、最初の式で得られた数値が挟まれる位置の番号であり、 dは、最初の式で得られた数値の小数部分です。

統計サンプルまたは母集団のパーセンタイルを求めるのは、多くの手順が必要なため複雑だと思われるかもしれませんが、実際には簡単です。次の 2 つの具体的な例を読んでいただければ、よりよく理解できると思います。

注: 科学界はパーセンタイルの計算方法についてまだ完全に合意していないため、少し異なる方法で説明している統計の本を見つけることができます。

パーセンタイルの計算例

上のサンプルのパーセンタイルを求める方法の説明で見たように、計算は最初の式の結果が 10 進数であるかどうかによって異なります。そのため、以下に解決済みの例を 2 つ、ケースごとに 1 つずつ示します。

例1

• 次の表に示すデータから、1、43、および 89 パーセンタイルを計算します。

前のセクションで説明したように、パーセンタイルの位置を見つけるための式は次のとおりです。

この場合、この演習のサンプル サイズは 999 統計データであるため、最初のパーセンタイルの位置を計算するには、 nに 999 を、 kに 1 を代入する必要があります。

したがって、最初のパーセンタイルは、累積絶対頻度が 10 よりすぐ大きいパーセンタイルになります。この場合、累積絶対頻度は 53 であるため、これは 35 になります。

43 パーセンタイルを決定するには、同じ式を使用する必要がありますが、明らかに、今回はkを 43 に置き換えます。

430 のすぐ上の絶対累積度数はデータ 39 の 431 であるため、43 パーセンタイルは 39 に等しくなります。

最後に、同じ式を適用して 89 パーセンタイルを取得します。

値 44 の累積絶対頻度は 948 で、890 よりすぐに大きいです。したがって、89 パーセンタイルは 44 になります。

例 2

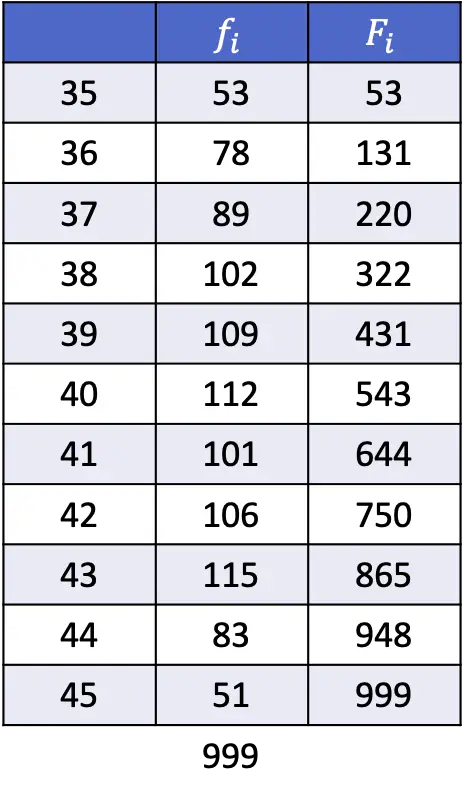
• 次のデータ系列の 35 パーセンタイルと 67 パーセンタイルを見つけます。

この演習ではさらに多くの計算を行う必要がある場合でも、原則は同じです。次の式を使用してパーセンタイル位置を計算する必要があります。

したがって、35 パーセンタイルを計算するには、 k を35 に置き換え、 n をデータの総数 (つまり 700) に置き換えます。

ただし、今回は数式から 10 進数を取得したため、正確なパーセンタイル値を計算するには次の代数式を適用する必要があります。

最初の式で与えられる数値は 245.35 であるため、35 パーセンタイルは位置 245 と 246 の間にあり、それぞれ値 29 と 29 に対応します。したがって、 x _iは 29、 x _i+1は 29、 dは得られた数値の小数部分、つまり 0.35 に相当します。

67 パーセンタイルを見つけるには、同じ方法を使用する必要があります。まずパーセンタイル位置を計算します。

結果の数値 469.67 は、パーセンタイルが位置 469 と 470 の間にあり、その値が 31 と 32 であることを示しています。 したがって、プロセスで 2 番目の式を使用して、正確なパーセンタイル値を見つけます。

パーセンタイル計算機

次の計算機に、計算する統計データ セットとパーセンタイル数を入力します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

• パーセンタイル =

グループ化されたデータのパーセンタイル

データが グループ にグループ化されているときにパーセンタイルを計算するには、まず次の式を使用してパーセンタイルが属するグループまたはクラスを見つける必要があります。

したがって、パーセンタイルは、絶対頻度が前の式で得られた数値よりもすぐに大きい区間内になります。

パーセンタイルが属する区間がわかったら、次の式を適用してパーセンタイルの正確な値を見つける必要があります。

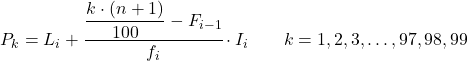
金：

• Ｌ _{ｉ は}、パーセンタイルが存在する間隔の下限である。
• nは観測値の総数です。
• F _i-1は、前の間隔の累積絶対頻度です。
• f _iは、パーセンタイルが含まれる間隔の絶対周波数です。
• I _iはパーセンタイル間隔の幅です。

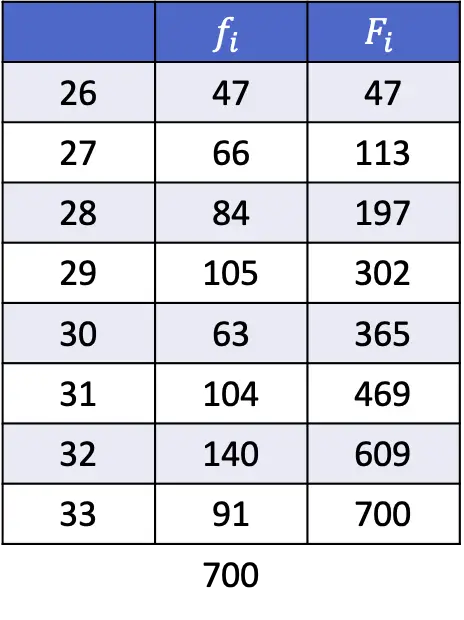
以下は、データが間隔で表される場合にパーセンタイルを取得する方法についての段階的な演習です。具体的には、29、52、98 パーセンタイルが計算されます。

このサンプルのデータは間隔としてグループ化されているため、パーセンタイルを決定するには 2 つの手順を実行する必要があります。まず、パーセンタイルが該当する間隔を見つけ、次に式を適用してパーセンタイルの正確な値を計算する必要があります。パーセンタイル。

したがって、次の式を使用して 29 パーセンタイルの位置を見つけます。

パーセンタイル間隔は、累積絶対頻度が 145.29 よりすぐ大きい間隔になります。この場合、累積絶対頻度が 175 である間隔 [350.375) です。パーセンタイル間隔がわかったら、次の公式を適用してその間隔を計算します。正確な値:

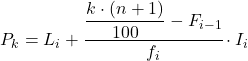
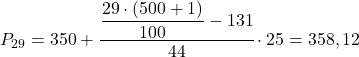
次に、同じ手順を繰り返して 52 パーセンタイルを計算します。まずその間隔を計算します。

その累積絶対頻度 (298) が 260.52 のすぐ上の値であるため、52 パーセンタイル間隔は [400.425) です。したがって、パーセンタイルの正確な値は次のようになります。

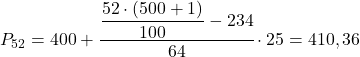
最後に、98 パーセンタイルを見つけます。いつものように、最初にそれが存在する間隔を計算します。

パーセンタイルが存在する間隔がわかったら、次の式を使用してその正確な値を計算します。