対応のある t 検定を手動で実行する方法
対のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。
次の段階的な例は、対応のあるサンプルの t 検定を実行して、次の 2 つのグループ間で母集団の平均が等しいかどうかを判断する方法を示しています。
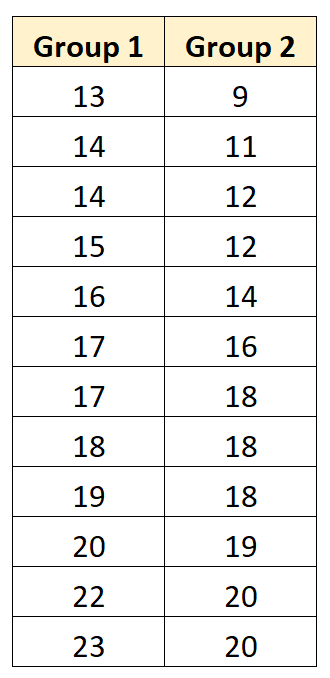
ステップ 1: 検定統計量を計算する
対応のある t 検定の検定統計量は次のように計算されます。
t = x diff / (s diff /√ n )
金:
- x diff :差の平均の例
- s:差の標準偏差の例
- n:サンプルサイズ (つまり、ペアの数)
2 つのグループ間の差の平均と 2 つのグループ間の差の標準偏差を計算します。
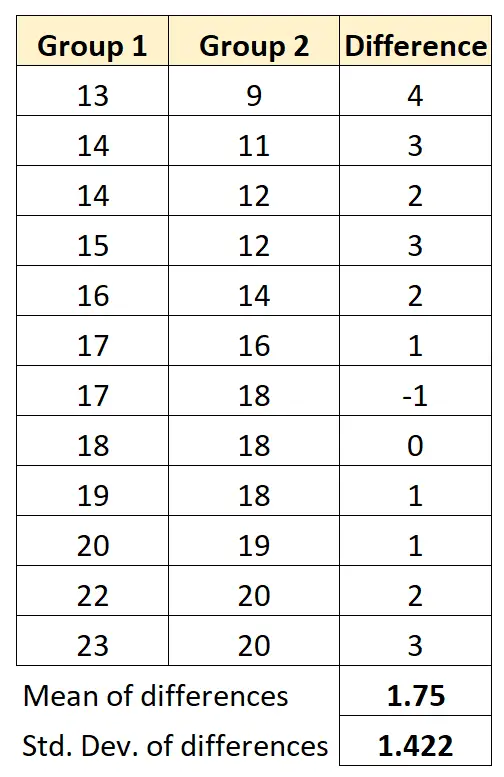
したがって、検定統計量は次のように計算できます。
- t = x diff / (s diff /√ n )
- t = 1.75 / (1.422/√ 12 )
- t = 4.26
ステップ 2: 臨界値を計算する
次に、テスト統計を比較するための臨界値を見つける必要があります。
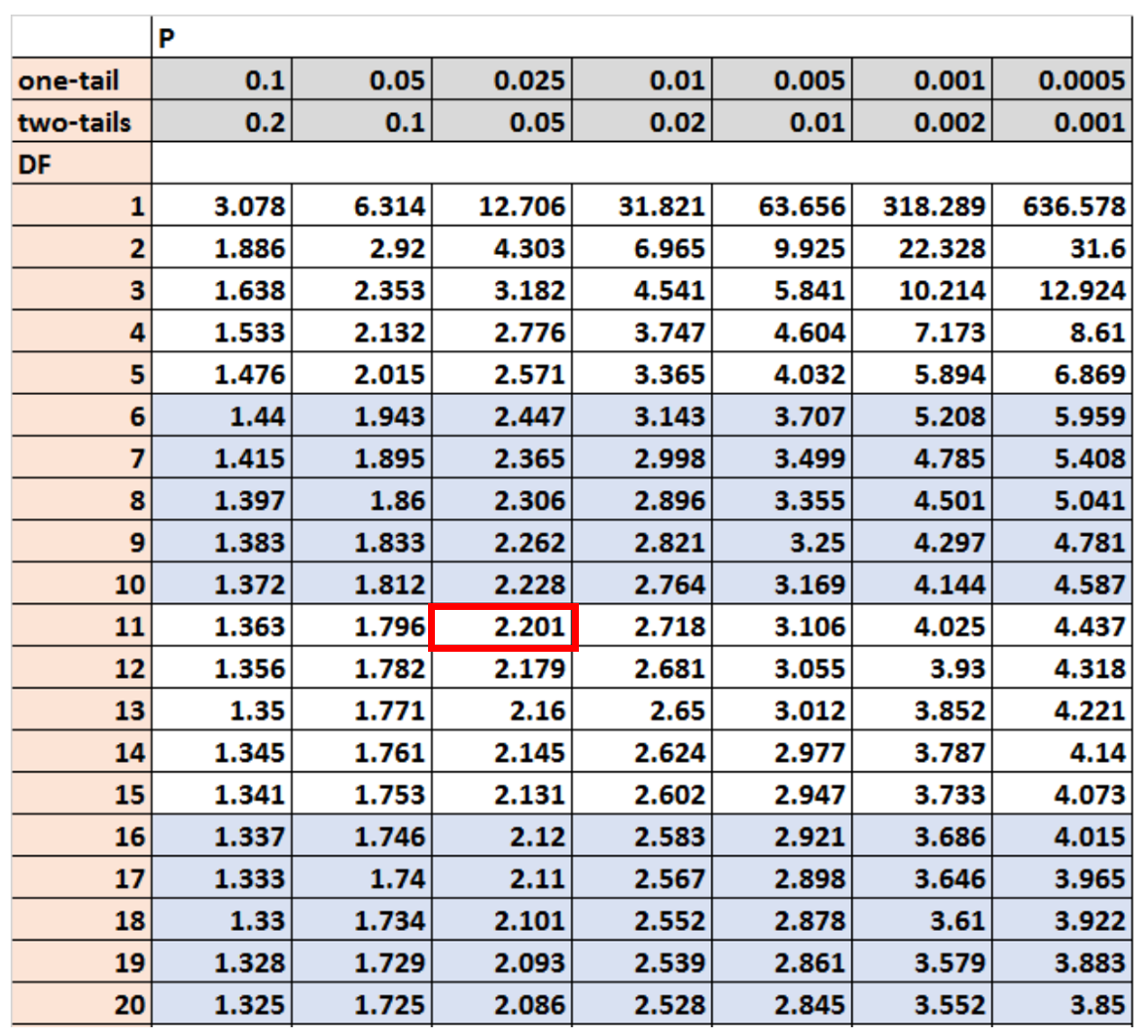
この例では、自由度 α = 0.05 および df = n-1 の両側検定を使用します。
t 分布表によると、これらの値に対応する臨界値は2.201です。
ステップ 3: 帰無仮説を棄却する、または棄却に失敗する
対応のあるサンプルの t 検定では、次の帰無仮説と対立仮説を使用します。
- H 0 : μ 1 = μ 2 (2 つの母集団平均は等しい)
- H A : μ 1 ≠ μ 2 (2 つの母集団平均は等しくありません)
検定統計量の絶対値 ( 4.26 ) は、t テーブルで見つかった臨界値 ( 2.201 ) より大きいため、帰無仮説を棄却します。
これは、2 つのグループ間の平均が等しくないと言える十分な証拠があることを意味します。
ボーナス:結果を確認するには、対応のあるサンプルの t 検定計算ツールを自由に使用してください。