ピアソン相関係数
この記事では、ピアソン相関係数 (または線形相関係数) とは何か、またその使用目的について説明します。ステップバイステップの演習とともに、ピアソン相関係数を計算する方法を学びます。さらに、最後にあるオンライン計算ツールを使用して、任意のデータセットのピアソン相関係数の値を見つけることができます。
ピアソンの相関係数とは何ですか?
ピアソン相関係数 は、線形相関係数または単に相関係数とも呼ばれ、2 つの変数間の関係を示す統計的尺度です。
2 つの変数間のピアソン相関係数を計算するには、これらの変数の共分散を分散の積の平方根で割る必要があります。
したがって、ピアソン相関係数は、2 つの量的確率変数間の線形依存性を定量化しようとします。演繹的に、変数間の相関を数値的に評価することは複雑である。なぜなら、ピューのように、ピアソンの相関係数の目的が変数間の関係を評価することである場合、変数のペアがより相関しているかどうかを判断するのが難しいからである。それらの間を比較してください。
ピアソン相関指数の値は -1 と +1 の間です。以下では、ピアソン相関係数の値がどのように解釈されるかを見ていきます。
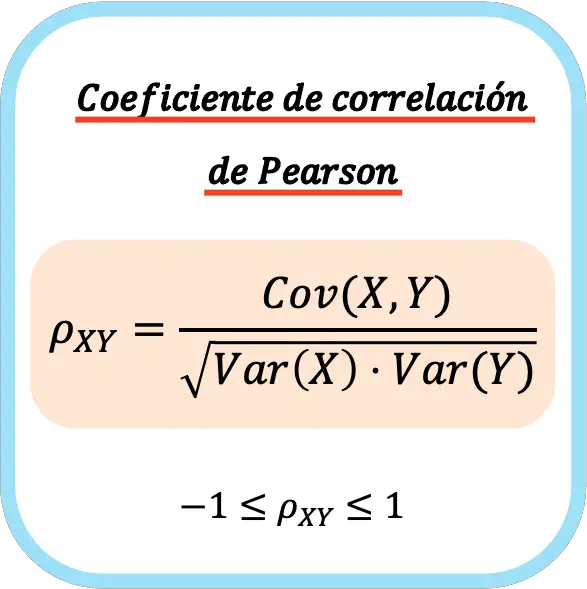
ピアソン相関係数式
2 つの統計変数のピアソン相関係数は、変数の共分散と各変数の分散の積の平方根との商に等しくなります。
したがって、ピアソン相関係数を計算する式は次のようになります。
👉以下の計算機を使用して、任意のデータセットのピアソン相関係数を計算できます。
ピアソン相関係数が母集団に対して計算される場合、通常、ギリシャ文字 ρ で表されます。ただし、サンプルを基準にして係数を計算する場合は、通常、文字 r が記号として使用されます。
ピアソン相関係数を決定するには、2 つの変数間の共分散と変数の分散を計算する方法を知っていることが不可欠であることに留意してください。さらに、これらの統計的測定が何を意味するのかを理解する必要があります。したがって、説明を続ける前に、次の 2 つの記事を読むことをお勧めします。
ピアソン相関係数の計算例
ピアソンの相関係数の定義とその式を考慮して、以下に段階的な例を示し、その計算方法を確認します。
- 次の 2 つの連続変数間のピアソン相関係数を計算します。

ピアソン相関係数を計算する前に、データセットを散布図で表して、2 つの変数間の関係を分析します。
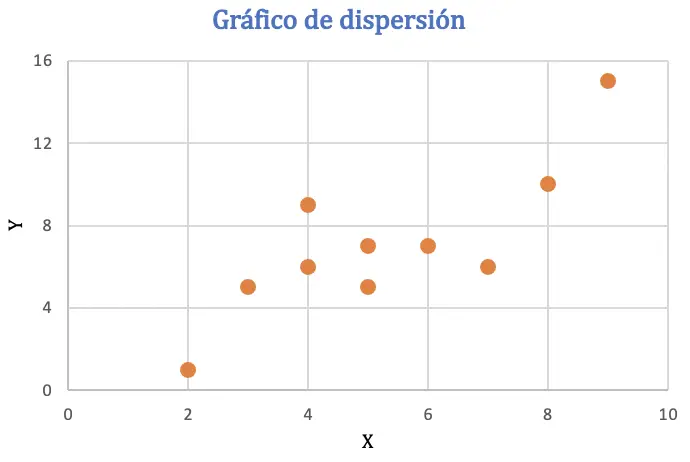
散布図から、データには正の傾向がある可能性がある、つまり、1 つの変数の値が増加すると、もう 1 つの変数も増加することが推測できます。相関関係を確認するには、ピアソン係数を求めます。
最初に行うことは、各変数の算術平均を個別に求めることです。これは、データの総和を観測値の数で割ったものに相当します。
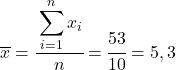
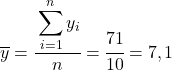
各変数の平均がわかったので、次の列をデータ テーブルに追加する必要があります。
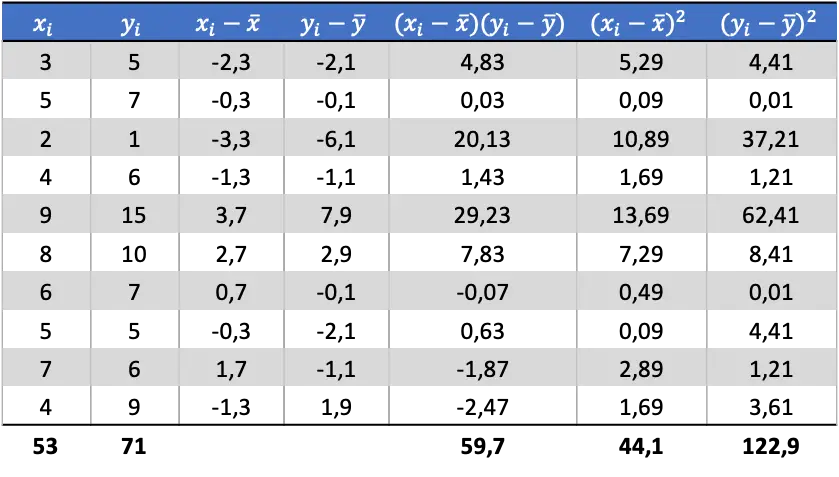
表内の計算されたデータから、共分散と分散の値を決定します (これがどのように行われたかを覚えていない場合は、これについて詳しく説明されている上に 2 つのリンクがあります)。
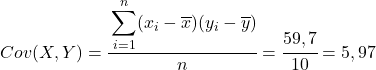
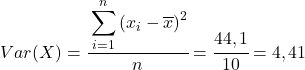
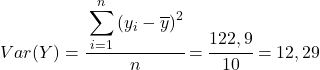
最後に、ピアソンの相関係数公式を適用してその値を取得します。
![]()
ピアソン相関係数は 1 に非常に近い値を持ちます。これは、これら 2 つの変数がかなり強い正の相関関係を持っていることを意味します。
これまで見てきたように、ピアソン相関係数を決定するには、Excel などのプログラムを使用して列計算をより迅速に実行すると非常に便利です。
ピアソン相関係数計算機
一連の統計データを次の計算機に入力して、2 つの変数間のピアソン相関係数を計算します。最初のボックスには 1 つの変数の値のみが含まれ、2 番目のボックスには 2 番目の変数の値のみが含まれるように、データのペアを分離する必要があります。
データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。
ピアソン相関係数の解釈
このセクションでは、ピアソン相関係数を解釈する方法を説明します。その値を知るだけでは十分ではなく、その意味を分析する方法を知っておく必要があるためです。
したがって、ピアソン相関係数の解釈はその値によって異なります。
- r=-1 : 2 つの変数には完全な負の相関があるため、すべての点がリンクする負の傾きを持つ線を描くことができます。
- -1<r<0 : 2 つの変数間の相関関係は負であるため、一方の変数が増加すると他方の変数は減少します。値が -1 に近づくほど、変数の負の関連性が高くなります。
- r=0 : 2 つの変数間の相関は非常に弱く、実際、それらの間の線形関係はゼロです。これは、変数が非線形関係を持つ可能性があるため、変数が独立していることを意味するものではありません。
- 0<r<1 : 2 つの変数間の相関は正で、値が +1 に近づくほど、変数間の関係が強くなります。この場合、一方の変数の値が増加すると、もう一方の変数の値も増加する傾向があります。
- r=1 : 2 つの変数には完全な正の相関関係があります。つまり、正の線形関係があります。
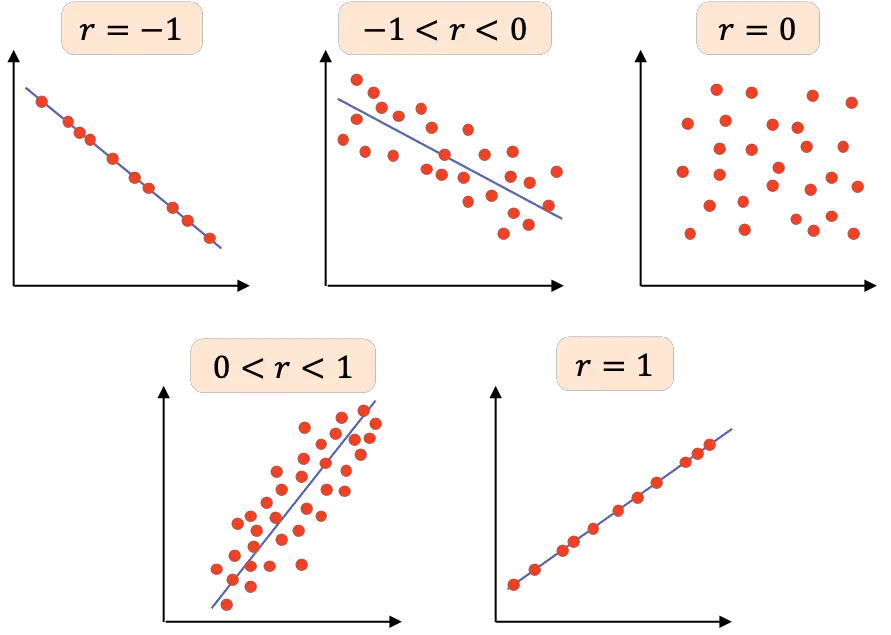
要約すると、ピアソン相関係数のさまざまな解釈を次の表に示します。
| 価値 | 解釈 |
|---|---|
| r=-1 | 完全な負の相関。 |
| -1<r<0 | 負の相関: 相関が -1 に近づくほど、相関が強くなります。 |
| r=0 | ゼロの線形相関。 |
| 0<r<1 | 正の相関: 相関が +1 に近づくほど、相関が強くなります。 |
| r=1 | 完全な正の相関関係。 |
2 つの変数間に関係がある場合でも、それはそれらの間に因果関係があることを意味するわけではないことに注意してください。つまり、2 つの変数間の相関関係は、変数の変化が変数の変化の原因であることを意味するわけではありません。他の変数。
たとえば、体内の 2 つの異なるホルモンの生成の間に正の関係があることがわかった場合、一方のホルモンの増加がもう一方のホルモンの増加につながる必要はありません。病気と闘うために両方のホルモンが必要で、したがって両方のホルモンのレベルが同時に上昇するため、体は両方のホルモンを生成している可能性があります。その場合、原因は病気になります。 2 つのホルモン間に因果関係があるかどうかを判断するには、さらなる研究を行う必要があります。