Excel でブルーシュ・ペイガン・テストを実行する方法
Breusch-Pagan 検定は、回帰分析に不均一分散性が存在するかどうかを判断するために使用されます。
このチュートリアルでは、Excel で Breusch-Pagan テストを実行する方法を説明します。
例: Excel での Breusch-Pagan テスト
この例では、10 人のバスケットボール選手の属性を記述する次のデータセットを使用します。
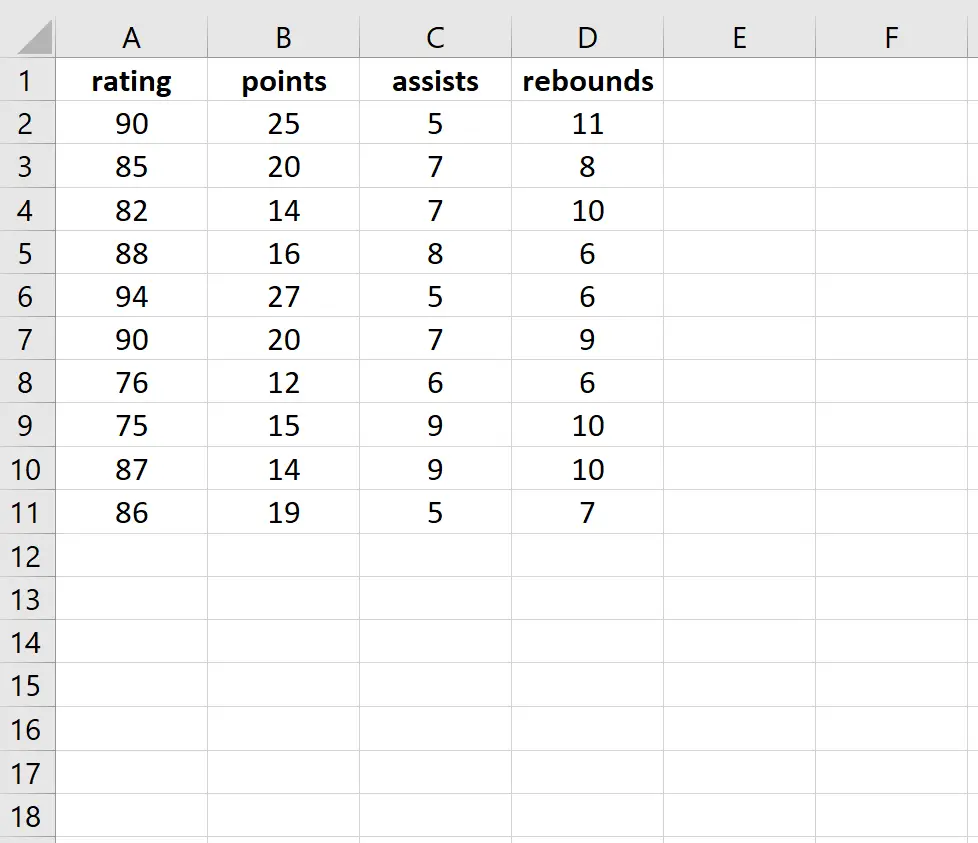
スコアを応答変数として、ポイント、アシスト、リバウンドを説明変数として使用して、重線形回帰モデルを当てはめます。次に、Breusch-Pagan 検定を実行して、回帰に不均一分散性が存在するかどうかを判断します。
ステップ 1: 重回帰を実行します。
Excel の上部のリボンで、[データ] タブに移動し、[データ分析] をクリックします。このオプションが表示されない場合は、まず無料の Analysis ToolPak ソフトウェアをインストールする必要があります。

「データ分析」をクリックすると、新しいウィンドウが表示されます。 「回帰」を選択し、「OK」をクリックします。応答変数と説明変数に必要なテーブルを入力し、「OK」をクリックします。
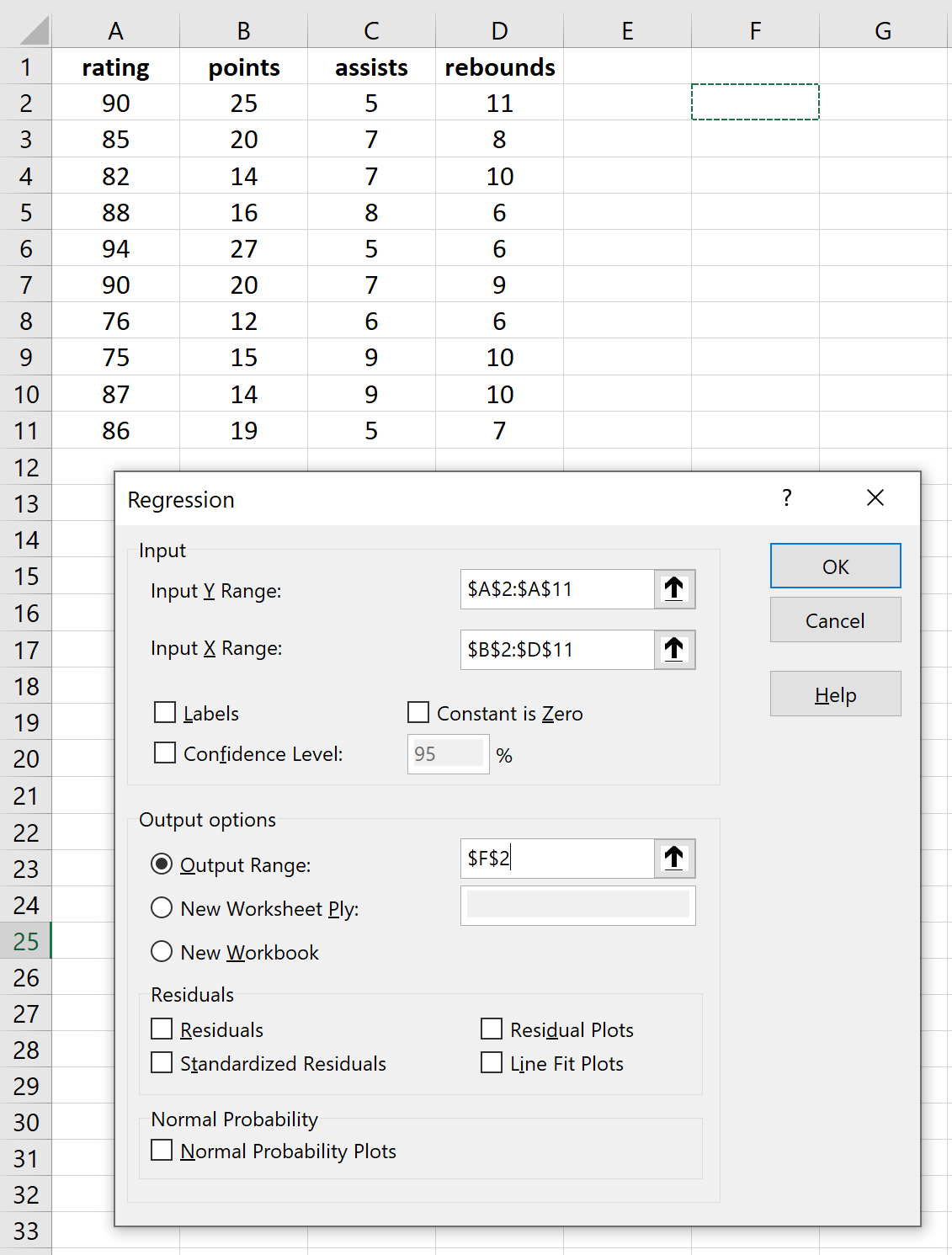
これにより、次の結果が生成されます。
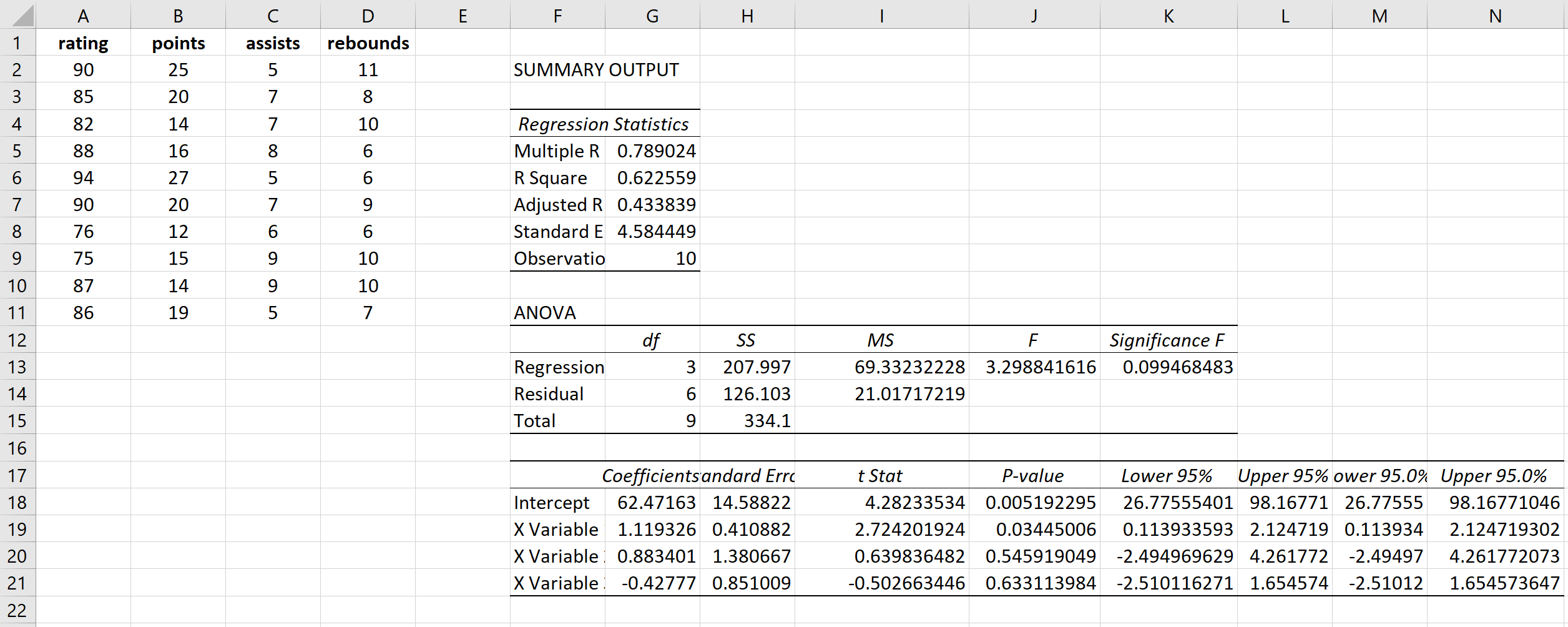
ステップ 2: 残差の二乗を計算します。
次に、各応答値の予測値と二乗残差を計算します。予測値を計算するには、回帰結果の係数を使用します。
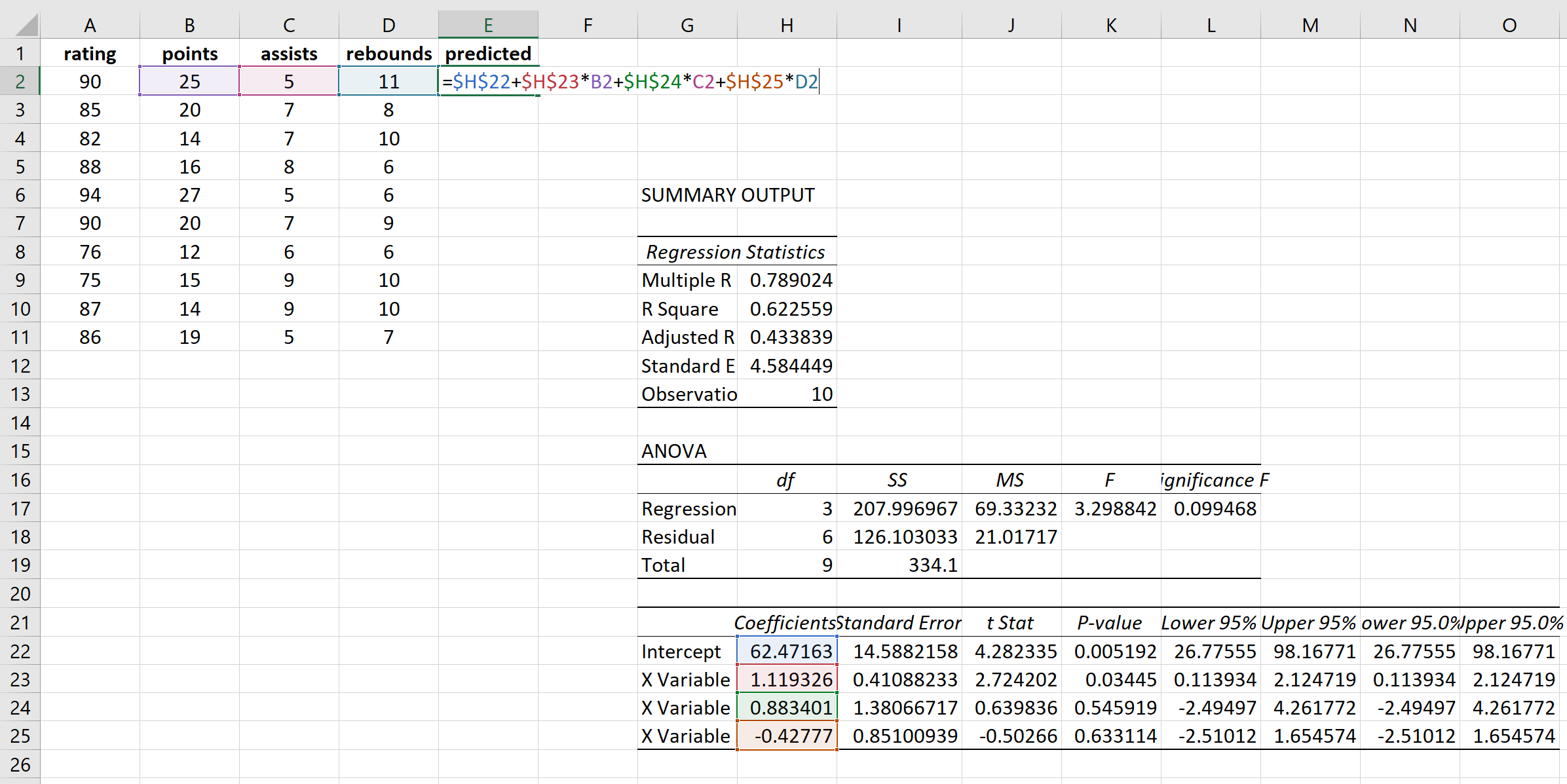
同じ式を使用して各予測値を取得します。
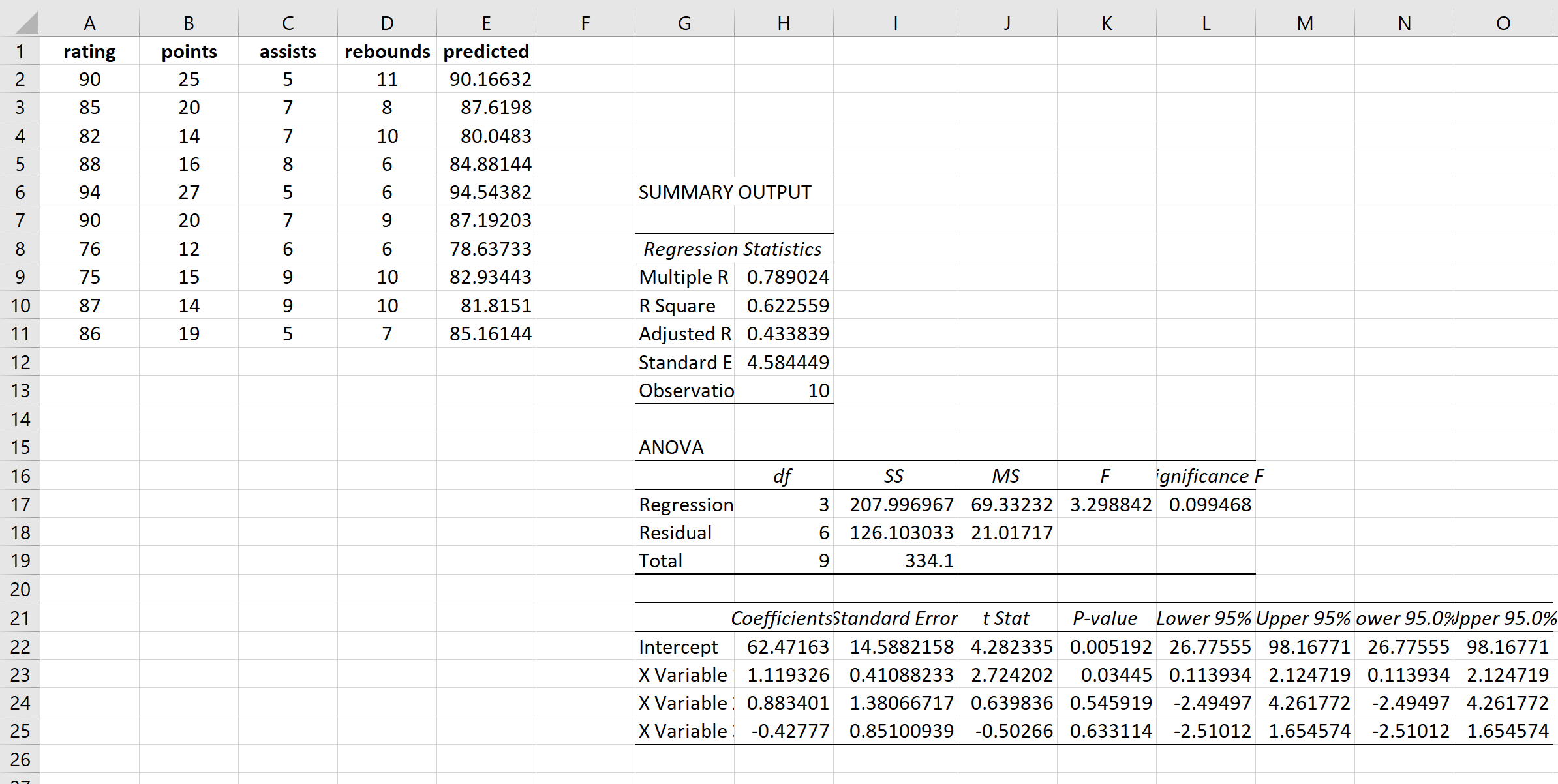
次に、各予測の残差の二乗を計算します。
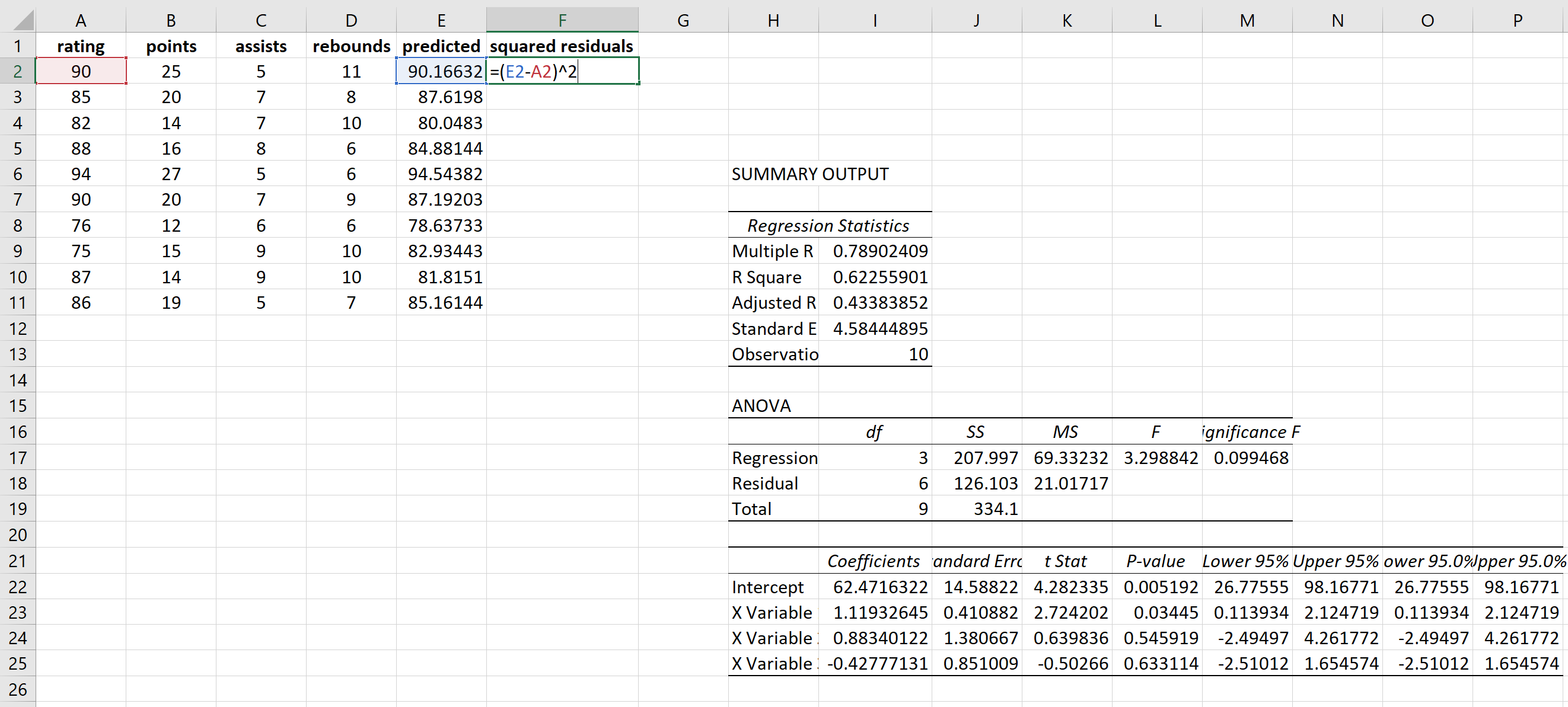
同じ式を使用して各残差平方を取得します。
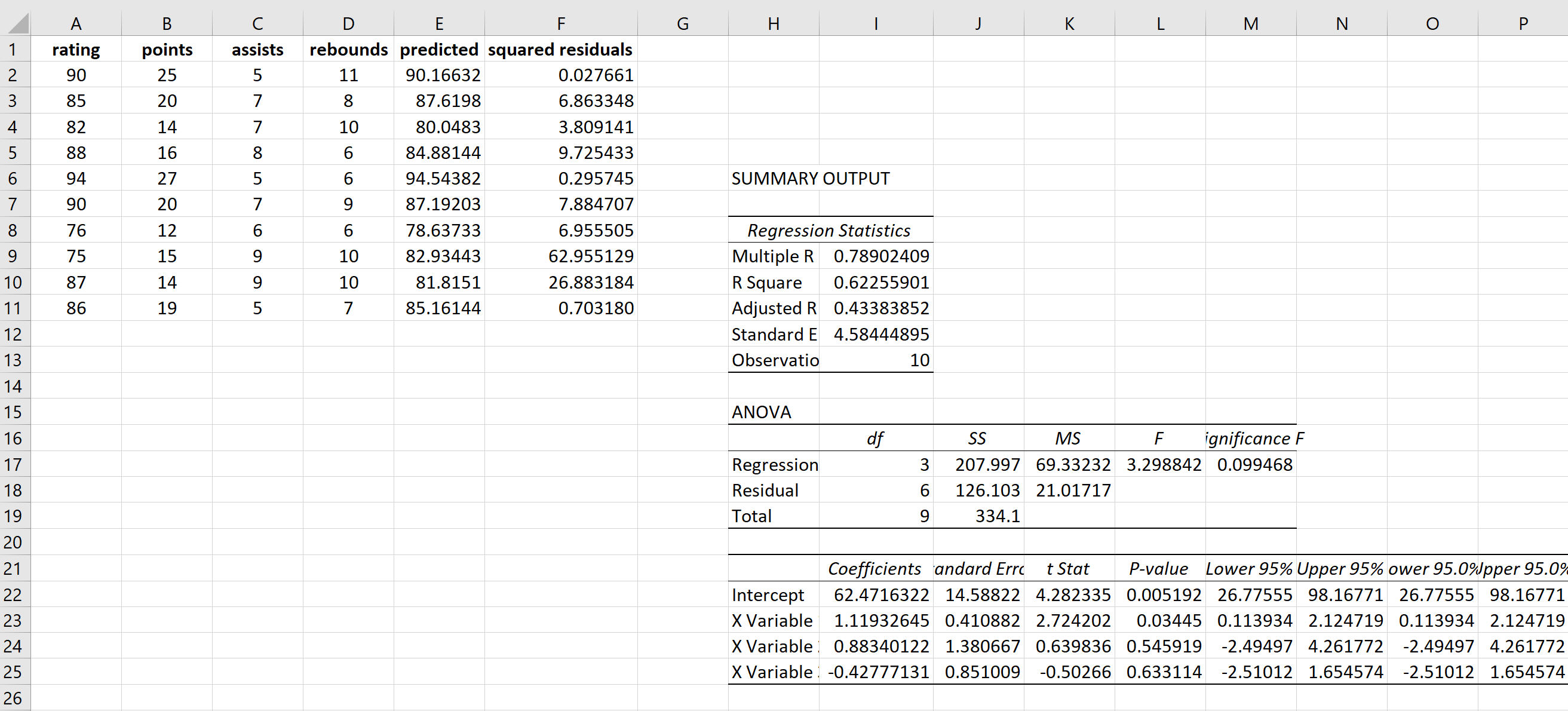
ステップ 3: 残差の 2 乗を応答値として使用して、新しい多重線形回帰を実行します。
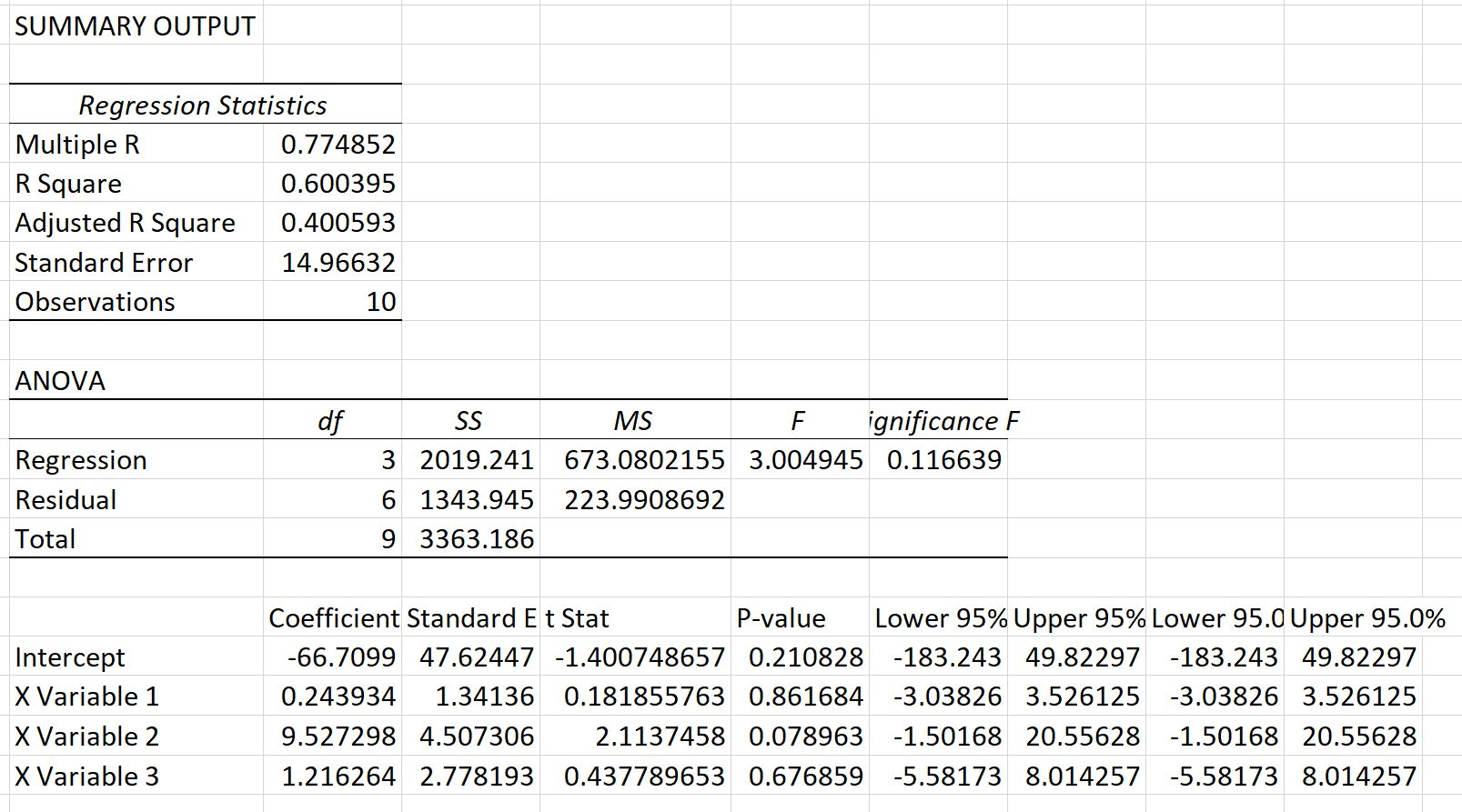
次に、前と同じ手順を実行して、ポイント、アシスト、リバウンドを説明変数として使用して重線形回帰を実行します。ただし、今回は残差の 2 乗を応答値として使用します。この回帰の結果は次のとおりです。
ステップ 4: ブリューシュ・パガン テストを実行します。
最後に、Breusch-Pagan 検定を実行して、元の回帰に不均一分散性が存在したかどうかを確認します。
まず、次の式を使用してカイ二乗検定統計量を計算します。
X 2 = n*R 2新しい
金:
n = 観測値の数
R 2 new = R 残差の二乗が応答変数として使用された「新しい」回帰の二乗。
この例では、 X2 = 10 * 0.600395 = 6.00395 です。
次に、この検定統計量に関連付けられた p 値を見つけます。これを行うには、Excel で次の数式を使用できます。
=CHISQ.DIST.RT(検定統計量、自由度)
この場合、自由度は出力の回帰dfに指定された数値です。この場合、それは 3 です。したがって、式は次のようになります。
=CHISQ.DIST.RT(6.00395, 3) = 0.111418 。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。元の回帰モデルに不均一分散性が存在すると主張する十分な証拠はありません。