R でブレイとカーティスの相違度を計算する方法

Bray-Curtis の相違度は、 2 つの異なるサイト間の相違度を測定する方法です。

これは、生態学や生物学において、2 つの場所で見られる種の観点から 2 つの場所の違いを定量化するためによく使用されます。

次のように計算されます。

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

金：

• C _ij :各サイトで見つかった種の最小値の合計。
• S _i :サイトiで計数された検体の総数
• S _j :サイトjで計数された検体の総数

ブレイとカーティスの相違度は常に 0 と 1 の間にあります。ここで、

• 0 は、2 つのサイトに非類似性がないことを示します。言い換えれば、各種類の種の数がまったく同じになります。
• 1 は、2 つのサイトが完全に類似していないことを示します。言い換えれば、それらは同じ種類の種を共有しません。

たとえば、植物学者が外出して、2 つの異なる場所で 5 つの異なる植物種 (A、B、C、D、および E) の数を数えたとします。

次の表は、彼女が収集したデータをまとめたものです。

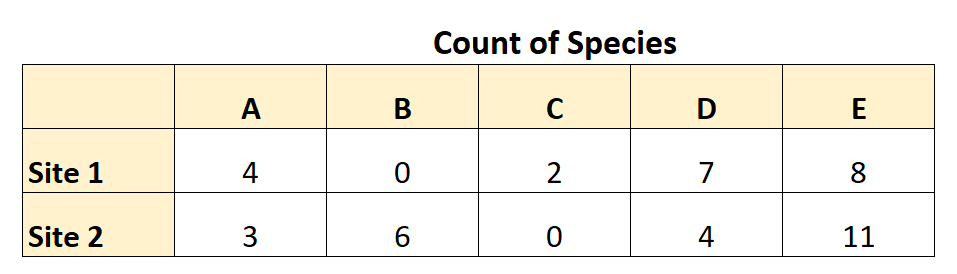
このデータを使用すると、次のようにブレイとカーティスの相違度を計算できます。

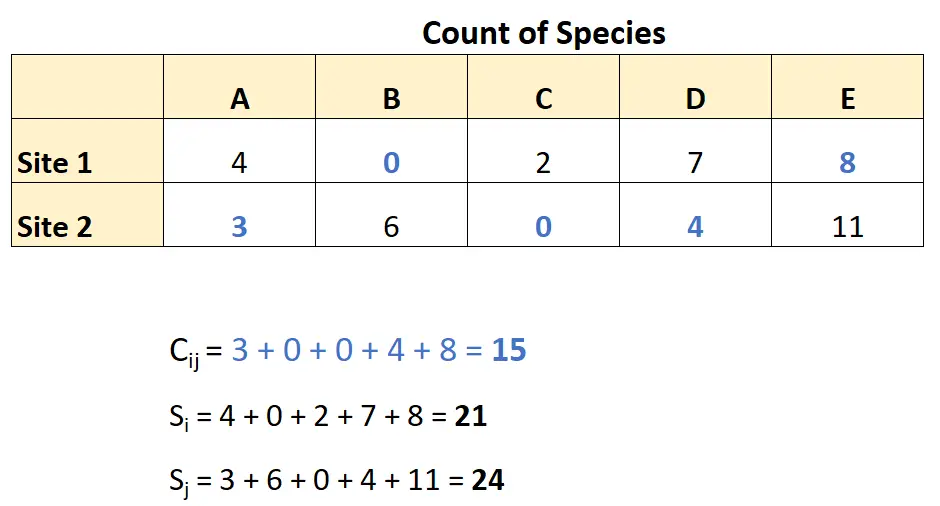
これらの数値を Bray-Curtis の相違度の公式に統合すると、次の結果が得られます。

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• BC _ij = 0.33

これら 2 つのサイト間の Bray-Curtis の相違度は0.33です。

次の例は、R で Bray-Curtis の相違度を計算する方法を示しています。

例: R でのブレイとカーティスの相違度の計算

まず、データ値を保持するために R で次のデータ フレームを作成しましょう。

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

次のコードを使用して、データ フレーム内の 2 つの行間の Bray-Curtis の非類似度を計算できます。

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

Bray-Curtis は0.33であることが判明しました。

これは、以前に手動で計算した値と一致します。

注: この数式は、データ フレーム内の各行が個別のサイトを表す場合にのみ機能します。

追加リソース

次のチュートリアルでは、R で他の類似性メトリクスを計算する方法を説明します。

R で Jaccard 類似度を計算する方法
R でコサイン類似度を計算する方法