ブレイとカーティスの相違点: 定義と例
J. Roger BrayとJohn Thomas Curtisにちなんで名付けられた、 Bray-Curtis の相違度は、2 つの異なるサイト間の相違度を測定する方法です。
これは、生態学や生物学において、2 つの場所で見られる種の観点から 2 つの場所の違いを定量化するためによく使用されます。
ブレイとカーティスの相違度は次のように計算されます。
BC ij = 1 – (2*C ij ) / (S i + S j )
金:
- C ij :各サイトで見つかった種の最小値の合計。
- S i :サイトiで計数された検体の総数
- S j :サイトjで計数された検体の総数
ブレイとカーティスの相違度は常に 0 と 1 の間にあります。ここで、
- 0 は、2 つのサイトに非類似性がないことを示します。言い換えれば、各種類の種の数がまったく同じになります。
- 1 は、2 つのサイトが完全に類似していないことを示します。言い換えれば、それらは同じ種類の種を共有しません。
次の例は、2 つのサイトの Bray-Curtis の相違度を計算する方法を示しています。
例: ブレイとカーティスの相違度の計算
植物学者が外出して、2 つの異なる場所で 5 つの異なる植物種 (A、B、C、D、および E) の数を数えたとします。
次の表は、彼女が収集したデータをまとめたものです。
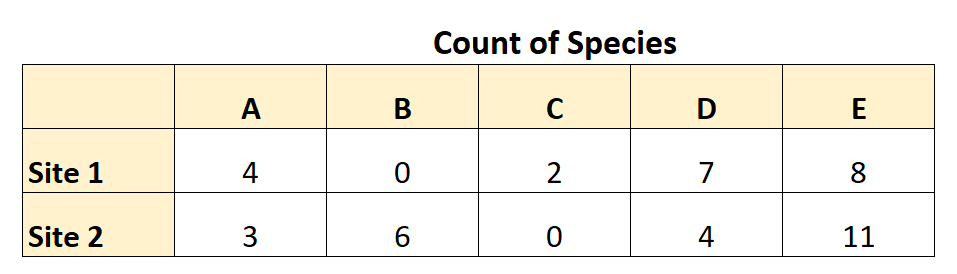
このデータを使用すると、次のようにブレイとカーティスの相違度を計算できます。
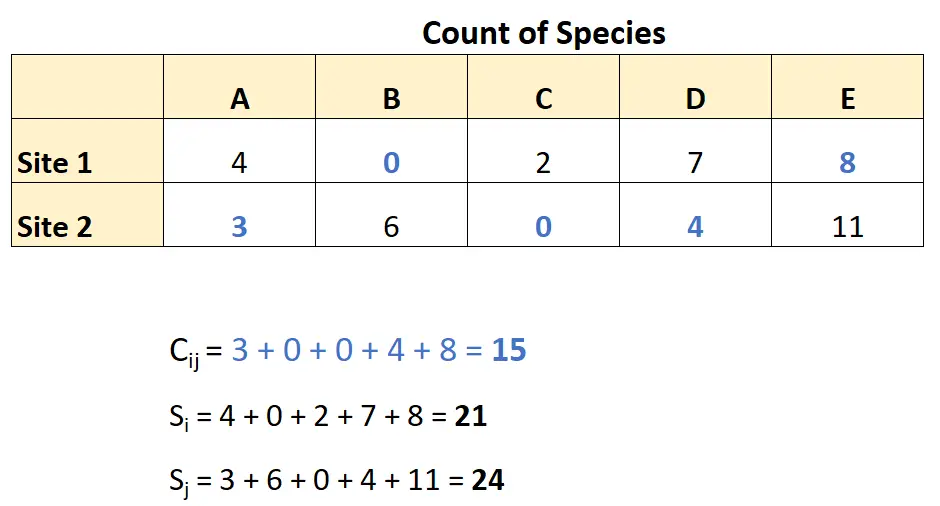
これらの数値を Bray-Curtis の相違度の公式に統合すると、次の結果が得られます。
- BC ij = 1 – (2*C ij ) / (S i + S j )
- BC ij = 1 – (2*15) / (21 + 24)
- BC ij = 0.33
これら 2 つのサイト間の Bray-Curtis の相違度は0.33です。
ブレイとカーティスの非類似性に関する重要な仮定
Bray-Curtis の非類似性は、2 つのサイトのサイズが等しいことを前提としています。
これは重要な仮定です。なぜなら、一方のサイトが他方のサイトよりも 4 倍大きい場合、カバーすべきエリアがはるかに多いため、当然、より大きなサイトには小さなサイトよりも多くの種が生息することになるからです。
これを説明するために、植物学者がデータを収集した場所の 1 つが他の場所よりも 4 倍大きいと仮定します。
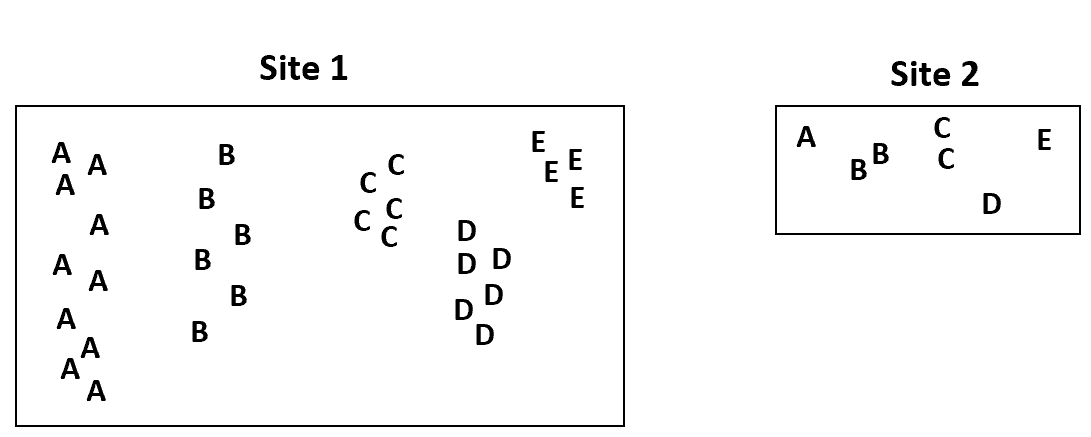
サイト 1 はサイト 2 よりもはるかに大きいため、サイト 1 では種の頻度がはるかに高くなることが予想されます。
したがって、ブレイとカーティスの相違度を計算すると、それは非常に大きくなります。ただし、2 つのサイトの違いはその構成ではなく、その規模にあるため、これは誤解を招く可能性があります。