統計におけるブロック: 定義と例
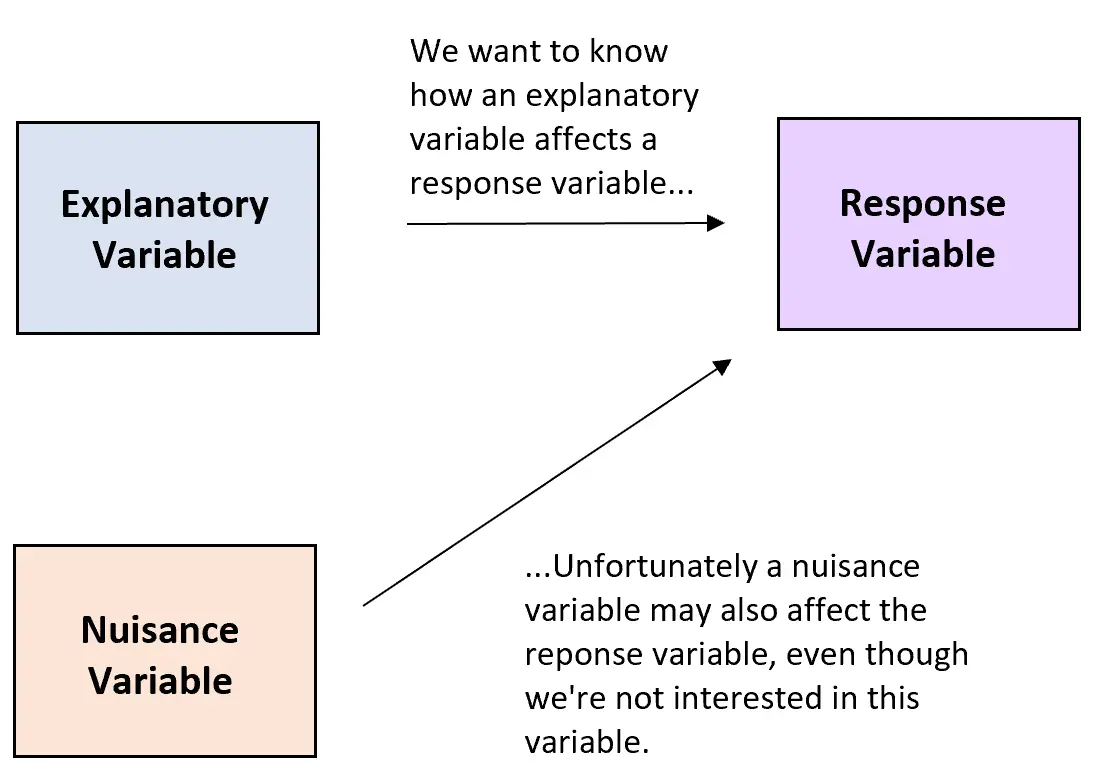
多くの場合、実験では、研究者は説明変数と応答変数の関係を理解したいと考えます。
残念ながら、実験研究では迷惑変数がよく現れます。迷惑変数は、説明変数と応答変数の間の関係に影響を与えるものの、研究者にとっては関心のない変数です。
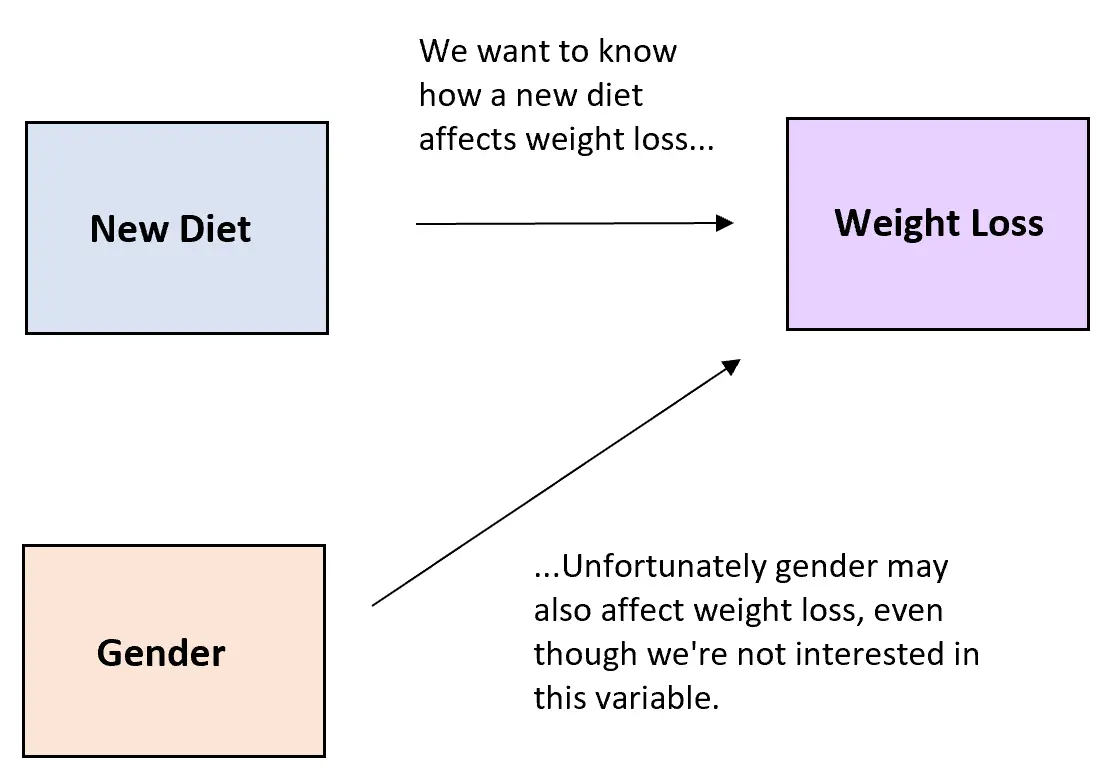
たとえば、研究者が体重減少に対する新しい食事の影響を理解したいと考えているとします。説明変数は新しい食事法、応答変数は体重減少の程度です。
ただし、変動を引き起こす可能性のある障害変数の 1 つは性別です。新しいダイエットが効果があるかどうかにかかわらず、個人の性別が体重の減少量に影響を与える可能性があります。
ブロックの概要
迷惑変数の影響を制御する一般的な方法は、迷惑変数の値に基づいて実験内の個人を分割するブロッキングを使用することです。
前の例では、次の 2 つのブロックのいずれかに個人を配置します。
- 男
- 女性
次に、各ブロック内で個人を次の 2 つの治療法のいずれかにランダムに割り当てます。
- 新しいダイエット
- 標準的な食事
こうすることで、各ブロック内の変動はすべての個人間の変動よりもはるかに小さくなり、性別をコントロールしながら新しい食事が減量にどのような影響を与えるかをよりよく理解できるようになります。
これを説明するために、研究に参加した 16 人の合計体重減少を示す次の表を考えてみましょう。
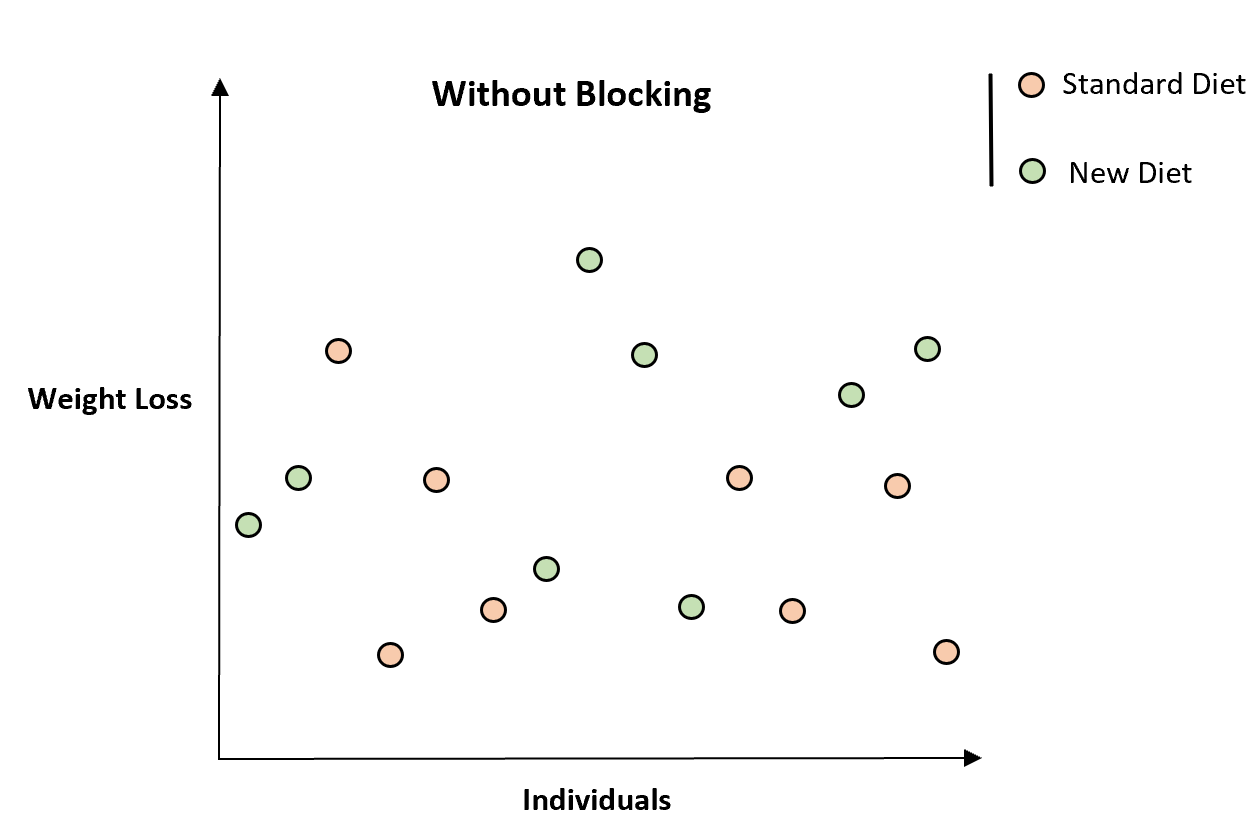
一見したところ、新しい食事療法が体重減少の増加と関連しているようには見えません。
しかし、性別に基づいて個人を 2 つのブロックに分けると、新しい食事が体重減少の増加と関連しているようであることが明らかになります。
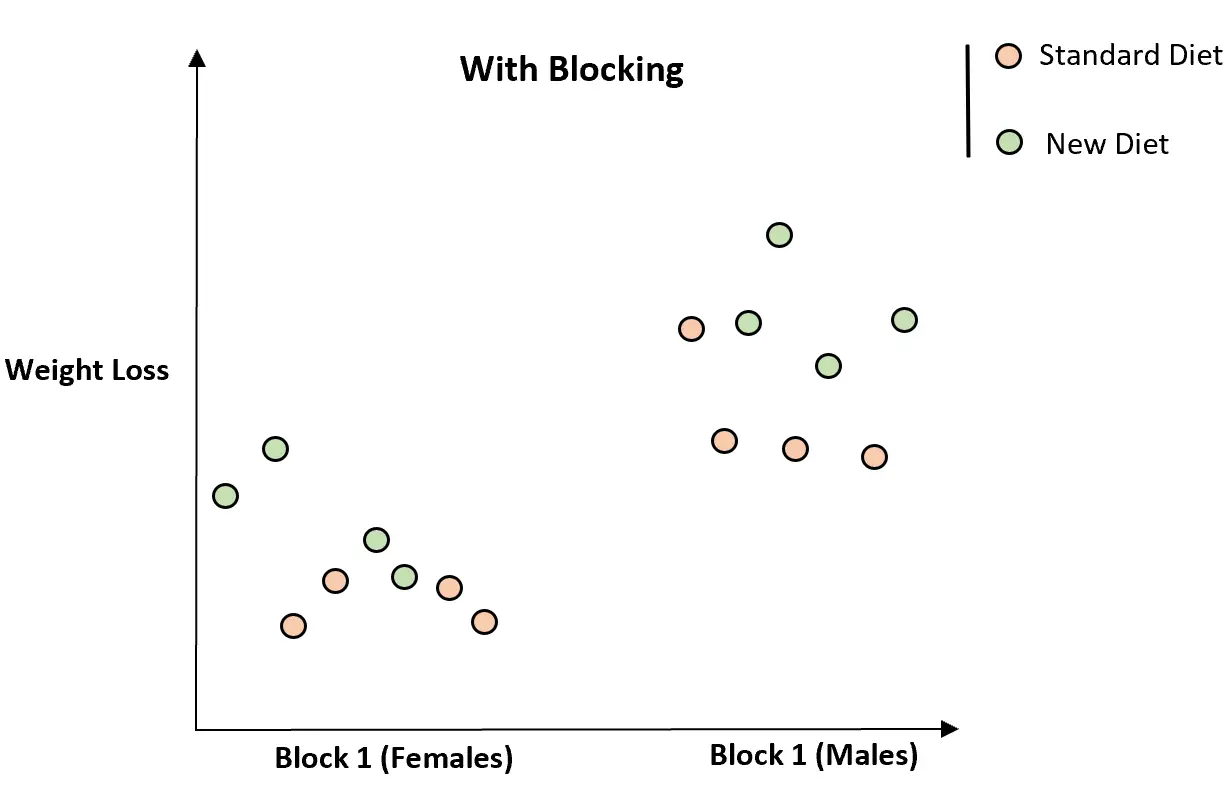
個人をブロックに分けることで、性別の無秩序な変数を制御できるため、新しい食事と体重減少の関係がより明確になりました。
その他のブロックの例
男性と女性ではさまざまな治療に対する反応が異なる傾向があるため、性別は実験で阻害要因として使用される一般的な迷惑変数です。
ただし、ブロック要因として使用できるその他の一般的な迷惑変数には次のようなものがあります。
- 年齢層
- 所得層
- 教育レベル
- 運動量
- 地域
実験の性質によっては、複数のブロック因子を同時に使用することも可能です。ただし、意味のある結果を得るには、ブロック因子が多いほどサンプルサイズが大きく必要になるため、実際には通常 1 つまたは 2 つだけが使用されます。
有害な変数と隠れた変数
前の例では、性別は既知の障害変数であり、研究者らは体重減少に影響すると考えていました。ただし、実験では多くの場合、隠れ変数も存在します。これは、説明変数と応答変数の間の関係にも影響を与える変数ですが、未知であるか、データを収集するのが難しいために単純に研究に含まれていない変数です。
たとえば、すべての人が、より体重を減らすために信頼できる生来の規律を持っていると仮定しましょう。規律を測定するのは難しいため、研究には阻害要因として含まれていませんが、規律を制御する 1 つの方法はランダム化を使用することです。
研究者は、個人を新しい食事または標準的な食事にランダムに割り当てることで、2 つのグループ間の個人の規律の全体的なレベルがほぼ等しくなる可能性を最大化できます。
したがって、ブロッキングを使用する実験では、潜在的な隠れた変数の影響を制御するために、個人をランダムに治療に割り当てることも重要です。