Excel でベイズの定理を適用する方法
ベイズの定理は、 2 つのイベントAとBについて次のように述べています。
P(A|B) = P(A)*P(B|A) / P(B)
金:
- P(A|B): イベント B が与えられた場合にイベント A が発生する確率。
- P(B|A): イベント A が発生した場合に、イベント B が発生する確率。
- P(A): イベント A の確率。
- P(B): イベント B の確率。
たとえば、天気が曇りである確率が 40% であるとします。また、特定の日に雨が降る確率が 20%、雨の日に雲が発生する確率が 85% であると仮定します。
特定の日に外が曇っている場合、その日に雨が降る確率はどれくらいですか?
解決策:
- P(曇り) = 0.40
- P(雨) = 0.20
- P(曇り | 雨) = 0.85
したがって、次のように計算できます。
- P(雨 | 曇り) = P(雨) * P(曇り | 雨) / P(曇り)
- P(雨 | 曇り) = 0.20 * 0.85 / 0.40
- P(雨 | 曇り) = 0.425
特定の日に外が曇りの場合、その日に雨が降る確率は0.425または42.5%です。
次の例は、Excel でベイズの定理を使用してこの問題を解決する方法を示しています。
例: Excel のベイズの定理
次の数式は、Excel でベイズの定理を適用する方法を示しています。
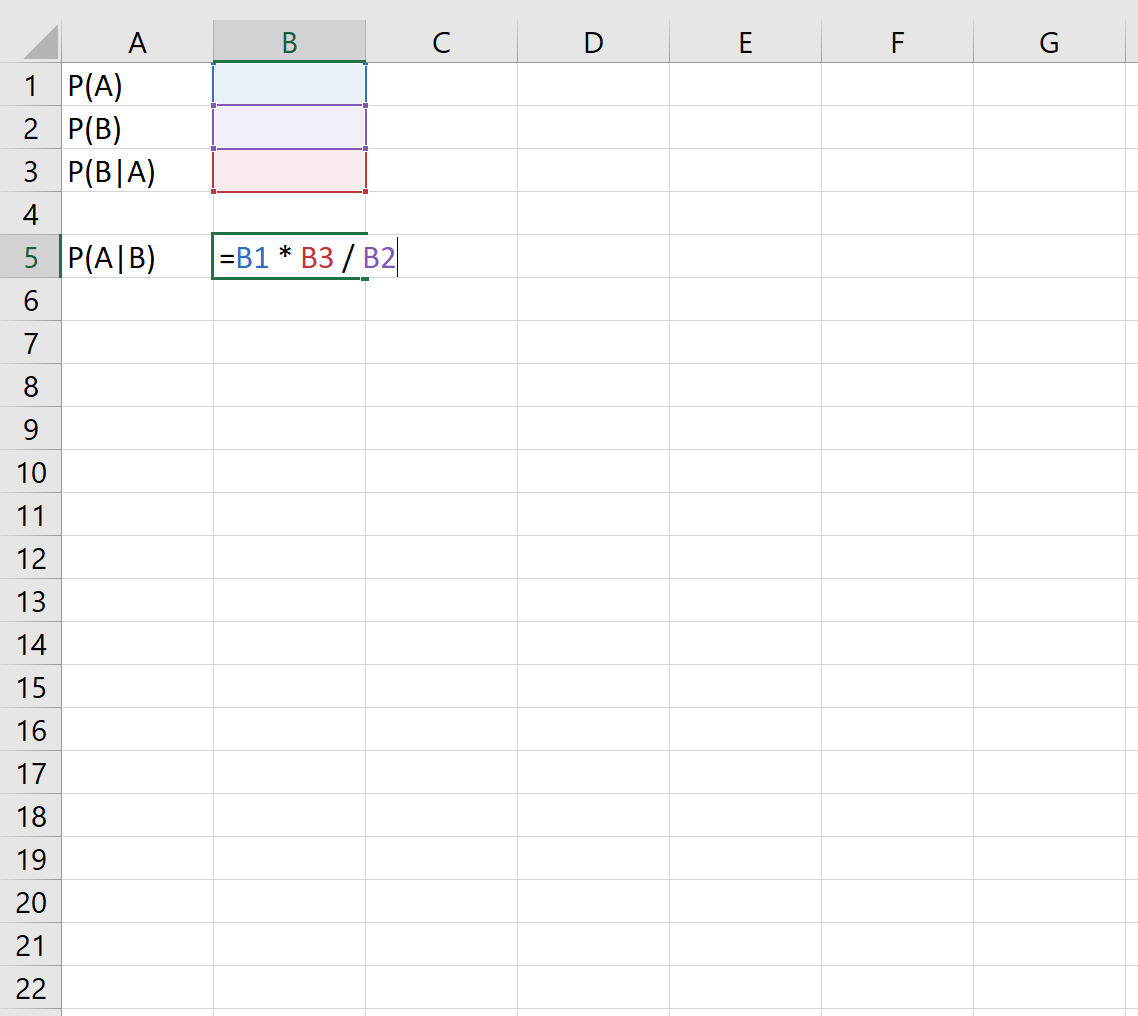
たとえば、次の確率がわかっているとします。
- P(曇り) = 0.40
- P(雨) = 0.20
- P(曇り | 雨) = 0.85
次に、それらを Excel のセルに接続するだけです。
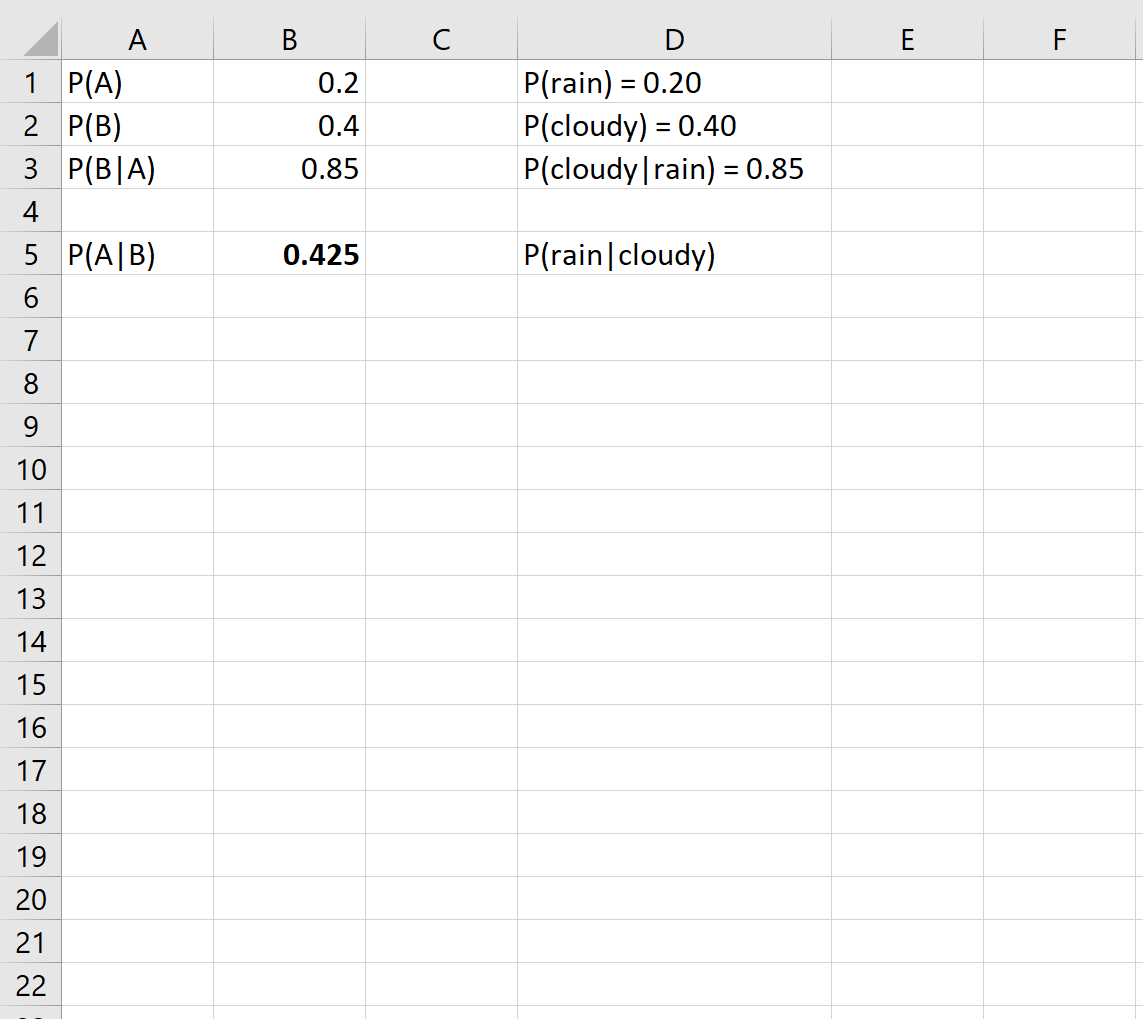
これは、特定の日に外が曇っている場合、その日に雨が降る確率は0.425または42.5%であることを示しています。