ベルヌーイ分布と二項分布: 違いは何ですか?
確率変数は、考えられる結果が 0 または 1 の 2 つだけである場合、ベルヌーイ分布に従います。
たとえば、コインを 1 回投げたとします。 pとします。これは、裏が出る確率が 1- pであることを意味します。
したがって、次のように書くことができます。
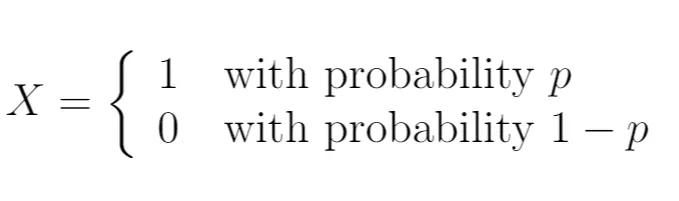
この場合、確率変数X はベルヌーイ分布に従います。取り得る値は 2 つだけです。
ここで、コインを複数回投げると、ベルヌーイ確率変数の合計は二項分布に従います。
たとえば、コインを 5 回投げて、 k回表が出る確率を知りたいとします。確率変数っぽいですね
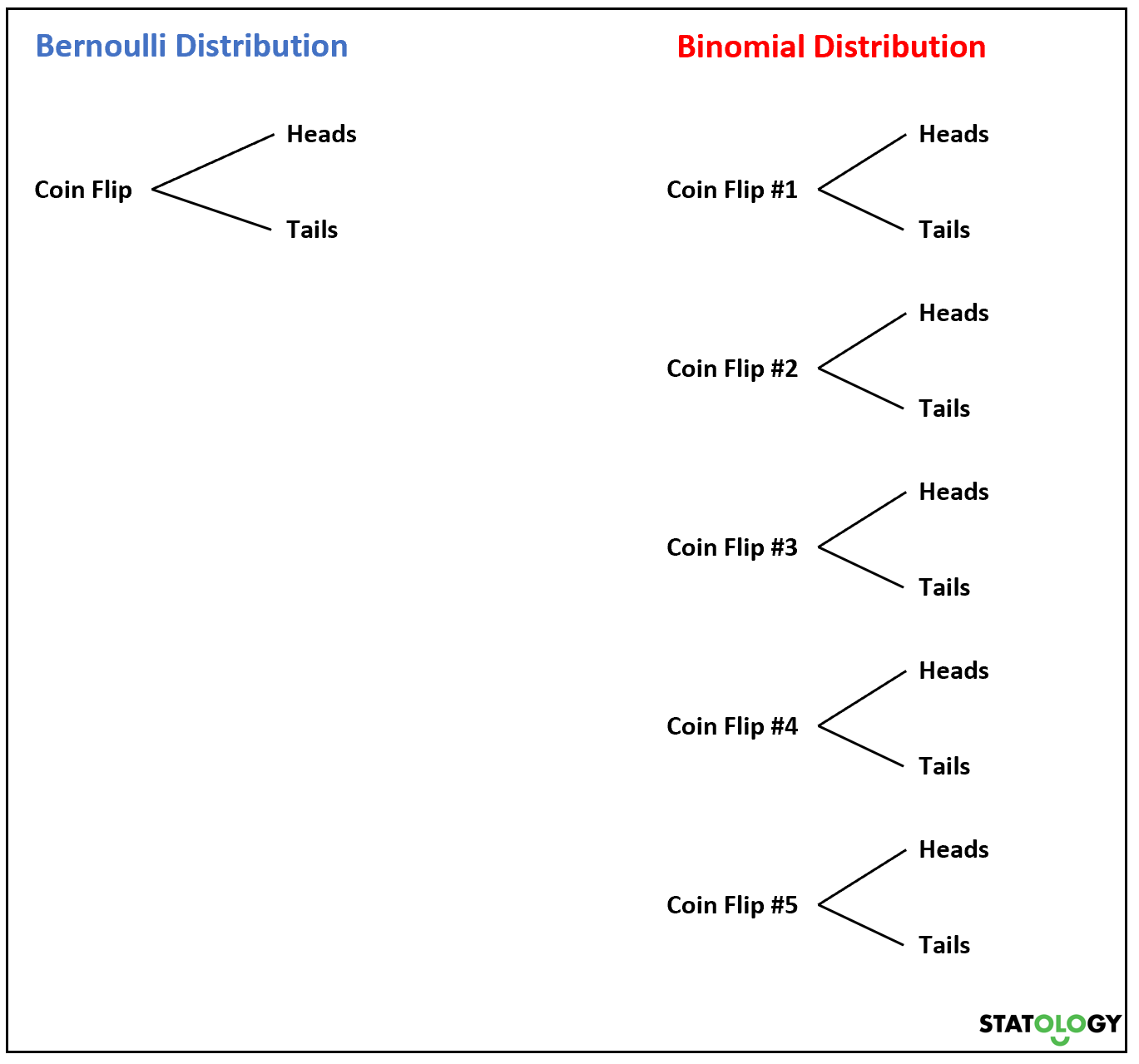
確率変数X が二項分布に従う場合、 X = kが成功する確率は次の式で求められます。
P(X=k) = n C k * p k * (1-p) nk
金:
- n:試行回数
- k:成功回数
- p:与えられた試行の成功確率
- n C k : n回の試行でk 個の成功を得る方法の数
たとえば、コインを3回投げたとします。上記の式を使用して、これら 3 回のフリップ中に表が 0 になる確率を決定できます。
P(X=0) = 3 C 0 * 0.5 0 * (1-0.5) 3-0 = 1 * 1 * (0.5) 3 = 0.125
n = 1 試行の場合、二項分布はベルヌーイ分布と等価です。
重要な注意事項
ベルヌーイ分布と二項分布に関する重要な注意事項をいくつか示します。
1. ベルヌーイ分布に従う確率変数は 2 つの可能な値のみを取ることができますが、二項分布に従う確率変数は複数の値を取ることができます。
たとえば、1 回のコイン トスでは、表が 0 か 1 になります。ただし、一連の 5 回の引き分けでは、表が 0、1、2、3、4、または 5 になる可能性があります。
2. 確率変数が二項分布に従うためには、各ベルヌーイ試行における「成功」の確率が等しく、独立している必要があります。
たとえば、「成功」を表で着地することと定義すると、各トスの成功確率は 0.5 であり、各トスは独立しています。つまり、あるトスの結果は別のトスの結果に影響を与えません。