統計におけるベータレベルとは何ですか? (定義&例)
統計学では、仮説検定を使用して、母集団パラメーターに関する仮説が正しいかどうかを判断します。
仮説検定には常に次の 2 つの仮説があります。
帰無仮説 (H 0 ):サンプル データは、母集団パラメーターに関する支配的な信念と一致します。
対立仮説 ( HA ):サンプル データは、帰無仮説で述べられた仮説が真ではないことを示唆しています。言い換えれば、ランダムではない原因がデータに影響を与えるということです。
仮説テストを実行すると、常に 4 つの結果が考えられます。
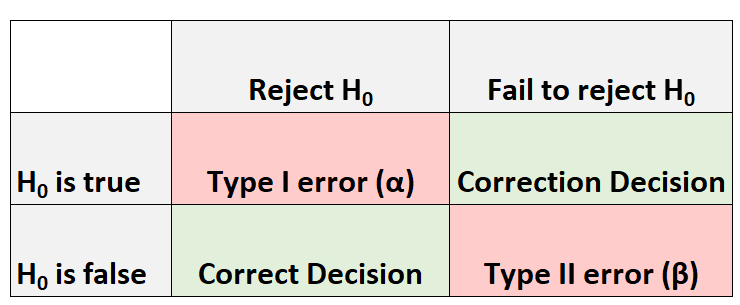
私たちが犯す可能性のある間違いには 2 つのタイプがあります。
- タイプ I エラー:帰無仮説が実際に真である場合、帰無仮説を棄却します。このコミットタイプのエラーの確率はαで示されます。
- タイプ II エラー:帰無仮説が実際には偽であるにもかかわらず、帰無仮説を棄却できません。このタイプのエラーがコミットされる確率はβで示されます。
アルファとベータの関係
理想的には、研究者は、タイプ I のエラーが発生する確率とタイプ II のエラーが発生する確率が低いことを望んでいます。
ただし、これら 2 つの確率の間には妥協点があります。アルファ レベルを下げると、帰無仮説が実際に正しい場合に帰無仮説を棄却する確率が下がる可能性がありますが、実際にはベータ レベル、つまり帰無仮説が間違っている場合に帰無仮説を棄却できない確率が増加します。
パワーとベータの関係
仮説検定の検出力とは、効果または差異が実際に存在する場合に、その効果または差異を検出する確率を指します。言い換えれば、それは偽の帰無仮説を正しく棄却する確率です。
次のように計算されます。
電力 = 1 – β
一般に研究者は、効果や差異がある場合にそれを検出できるように、テストの検出力が高いことを望んでいます。
上記の方程式から、テストの検出力を高める最善の方法はベータ レベルを下げることであることがわかります。そして、ベータレベルを下げる最善の方法は、通常、サンプルサイズを増やすことです。
次の例は、仮説検定のベータ レベルを計算する方法を示し、サンプル サイズを増やすとベータ レベルが低下する理由を示します。
例 1: 仮説検定のベータを計算する
研究者が、工場で生産されるウィジェットの平均重量が 500 オンス未満であるかどうかをテストしたいとします。重みの標準偏差が 24 オンスであることがわかっているため、研究者は 40 個のウィジェットのランダム サンプルを収集することにしました。
α = 0.05 で次の仮説が実現されます。
- H 0 : μ = 500
- H A : μ < 500
ここで、作成されたウィジェットの平均重量が実際に 490 オンスであると想像してください。言い換えれば、帰無仮説は棄却されなければなりません。
次の手順を使用して、ベータ レベル、つまり帰無仮説が実際には棄却されるべきときに棄却されない確率を計算できます。
ステップ 1: 非拒否領域を見つけます。
臨界 Z 値計算ツールによると、α = 0.05 での左側の臨界値は-1.645です。
ステップ 2: 拒否できない最小限のサンプルを見つけます。
検定統計量は、z = ( x – μ) / (s/ √n ) として計算されます。
したがって、サンプル平均を求めるこの方程式を解くことができます。
- x = μ – z*(s/ √n )
- x = 500 – 1.645*(24/ √40 )
- x = 493.758
ステップ 3: 最小サンプル平均が実際に発生する確率を決定します。
この確率は次のように計算できます。
- P(Z ≥ (493.758 – 490) / (24/√ 40 ))
- P(Z ≥ 0.99)
通常の CDF 計算機によると、Z ≥ 0.99 である確率は0.1611です。
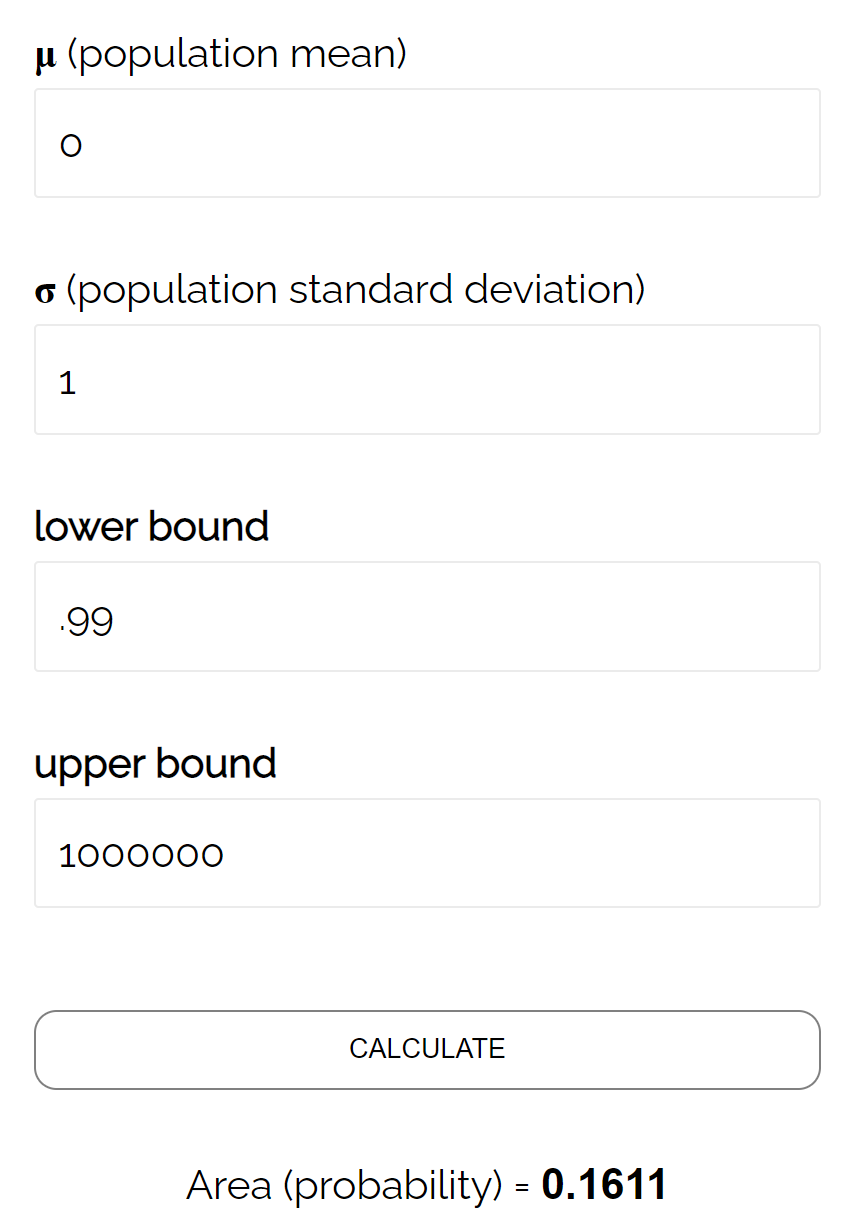
したがって、このテストのベータ レベルはβ = 0.1611 です。これは、実際の平均が 490 オンスの場合、違いが検出されない可能性が 16.11% あることを意味します。
例 2: サンプルサイズが大きいテストのベータを計算する
ここで、研究者がまったく同じ仮説検定を実行するが、代わりに n = 100 個のウィジェットのサンプルを使用すると仮定します。同じ 3 つの手順を繰り返して、このテストのベータ レベルを計算できます。
ステップ 1: 非拒否領域を見つけます。
臨界 Z 値計算ツールによると、α = 0.05 での左側の臨界値は-1.645です。
ステップ 2: 拒否できない最小限のサンプルを見つけます。
検定統計量は、z = ( x – μ) / (s/ √n ) として計算されます。
したがって、サンプル平均を求めるこの方程式を解くことができます。
- x = μ – z*(s/ √n )
- x = 500 – 1.645*(24/√ 100 )
- x = 496.05
ステップ 3: 最小サンプル平均が実際に発生する確率を決定します。
この確率は次のように計算できます。
- P(Z ≥ (496.05 – 490) / (24/√ 100 ))
- P(Z ≧ 2.52)
通常の CDF 計算機によると、Z ≥ 2.52 である確率は0.0059 です。
したがって、このテストのベータ レベルはβ = 0.0059 です。これは、実際の平均が 490 オンスの場合、違いが検出されない可能性は 0.59% のみであることを意味します。
サンプル サイズを 40 から 100 に増やすだけで、研究者はベータ レベルを 0.1611 から 0.0059 に下げることができたことに注目してください。
ボーナス:このタイプ II エラー計算ツールを使用して、テストのベータ レベルを自動的に計算します。