Sas で box-cox 変換を実行する方法
ボックス コックス変換は、非正規分布のデータ セットをより正規分布のセットに変換するために一般的に使用される方法です。
この方法の基本的な考え方は、次の式を使用して、変換されたデータができるだけ正規分布に近づくような λ の値を見つけることです。
- y(λ) = (y λ – 1) / λ (y ≠ 0 の場合)
- y = 0の場合、y(λ) = log(y)
PROC TRANSREGプロシージャを使用して、SAS の λ に使用する最適な値を特定できます。
次の例は、この手順を実際に使用する方法を示しています。
例: SAS のボックス-コックス変換
SAS に次のデータセットがあると仮定します。
/*create dataset*/ data my_data; input xy; datalines ; 7 1 7 1 8 1 3 2 2 2 4 2 4 2 6 2 6 2 7 3 5 3 3 3 3 6 5 7 8 8 ; run; /*view dataset*/ proc print data =my_data;
PROC REGを使用して、 x を予測変数として、 y を応答変数として使用して、単純な線形回帰モデルをこのデータセットに近似するとします。
/*fit simple linear regression model*/ proc reg data =my_data; model y = x; run ;
出力診断プロットでは、残差対分位点プロット(中央の行の一番左のプロット) を表示して、残差がモデル内でほぼ正規分布しているかどうかを確認できます。
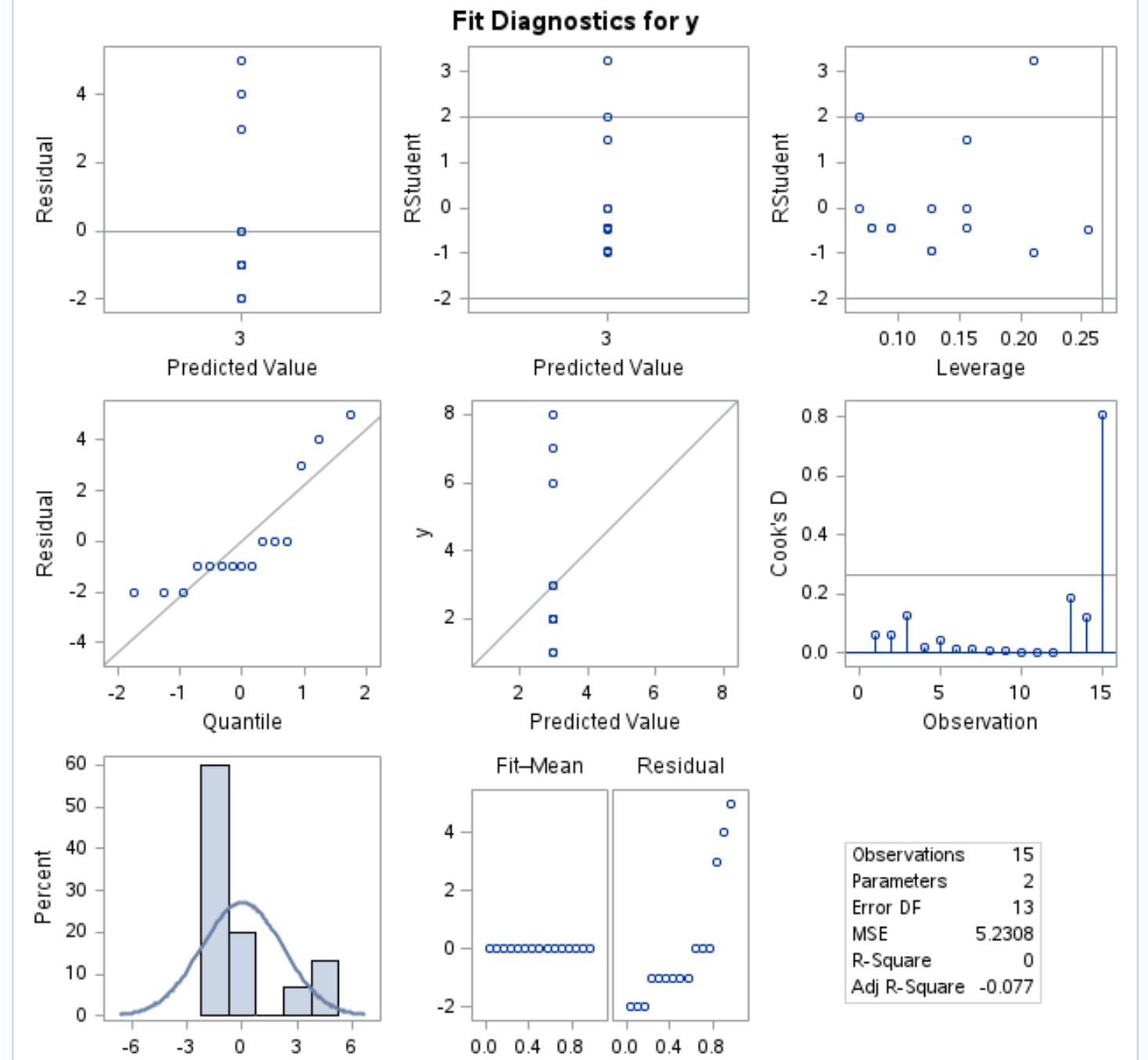
残差がほぼグラフの右対角線に沿って存在する場合、一般に残差は正規分布していると仮定します。
グラフから、残差が直線の対角線にあまり従っていないことがわかります。
これは、回帰モデルの応答変数が正規分布ではない可能性が高いことを示しています。
応答変数は正規分布ではないため、 PROC TRANSREGを使用して λ の値を特定し、応答変数をより正規分布になるように変換するために使用できます。
/*perform box-cox transformation*/ proc transreg data =my_data; model boxcox (y) = identity (x); run ;
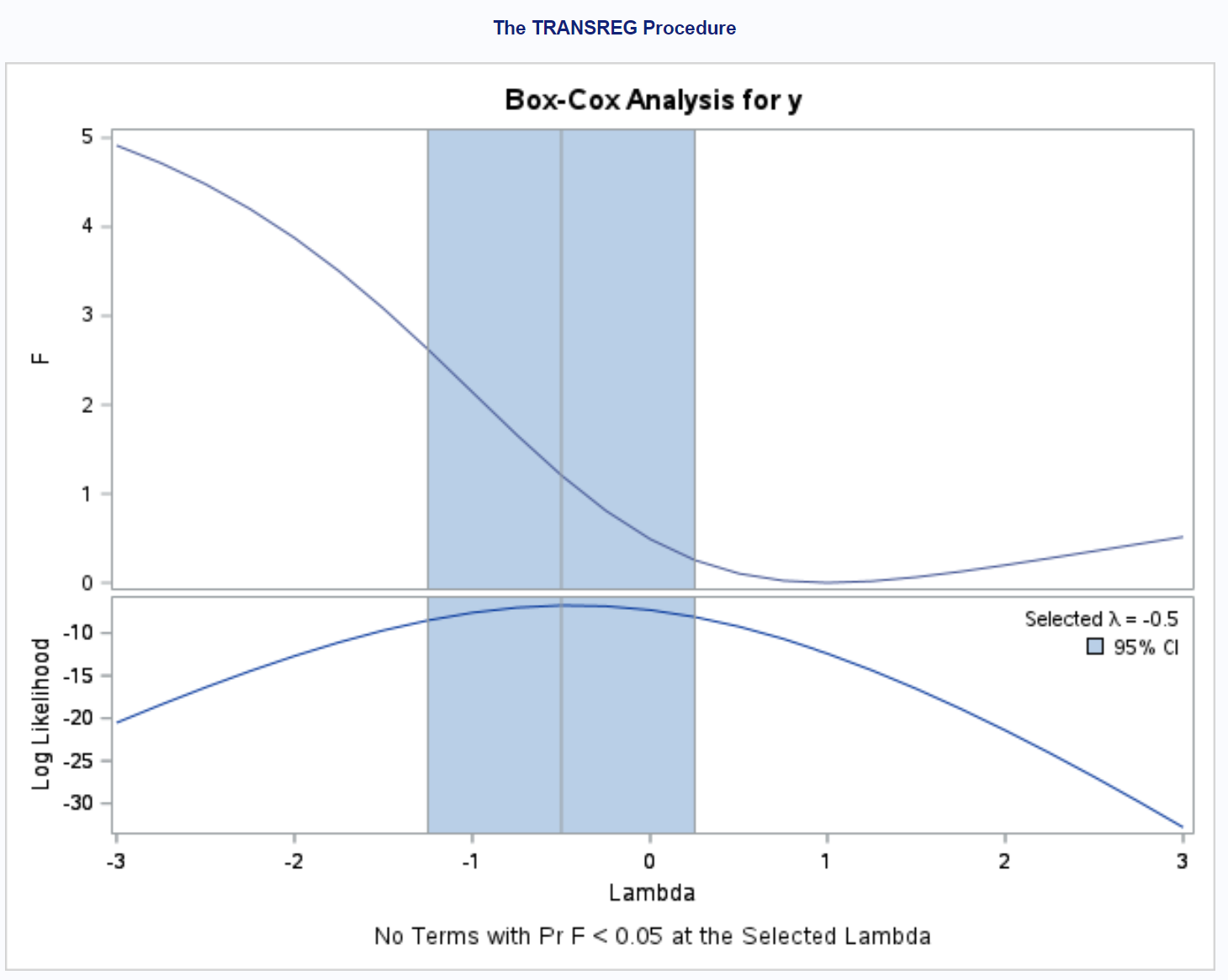
出力は、 λ に使用するために選択された値が – 0.5であることを示しています。
したがって、元の応答変数y を変数y = (y -0.5 – 1) / -0.5に置き換えることによって、単純な線形回帰モデルを近似できます。
次のコードは、これを行う方法を示しています。
/*create new dataset that uses box-cox transformation to create new y*/
data new_data;
set my_data;
new_y = (y**(-0.5) - 1) / -0.5;
run ;
/*fit simple linear regression model using new response variable*/
proc reg data =new_data;
model new_y = x;
run ;
残留 vs.このモデルの出力の分位点プロットでは、残差が直線の対角線に沿ってより密接に配置されていることがわかります。
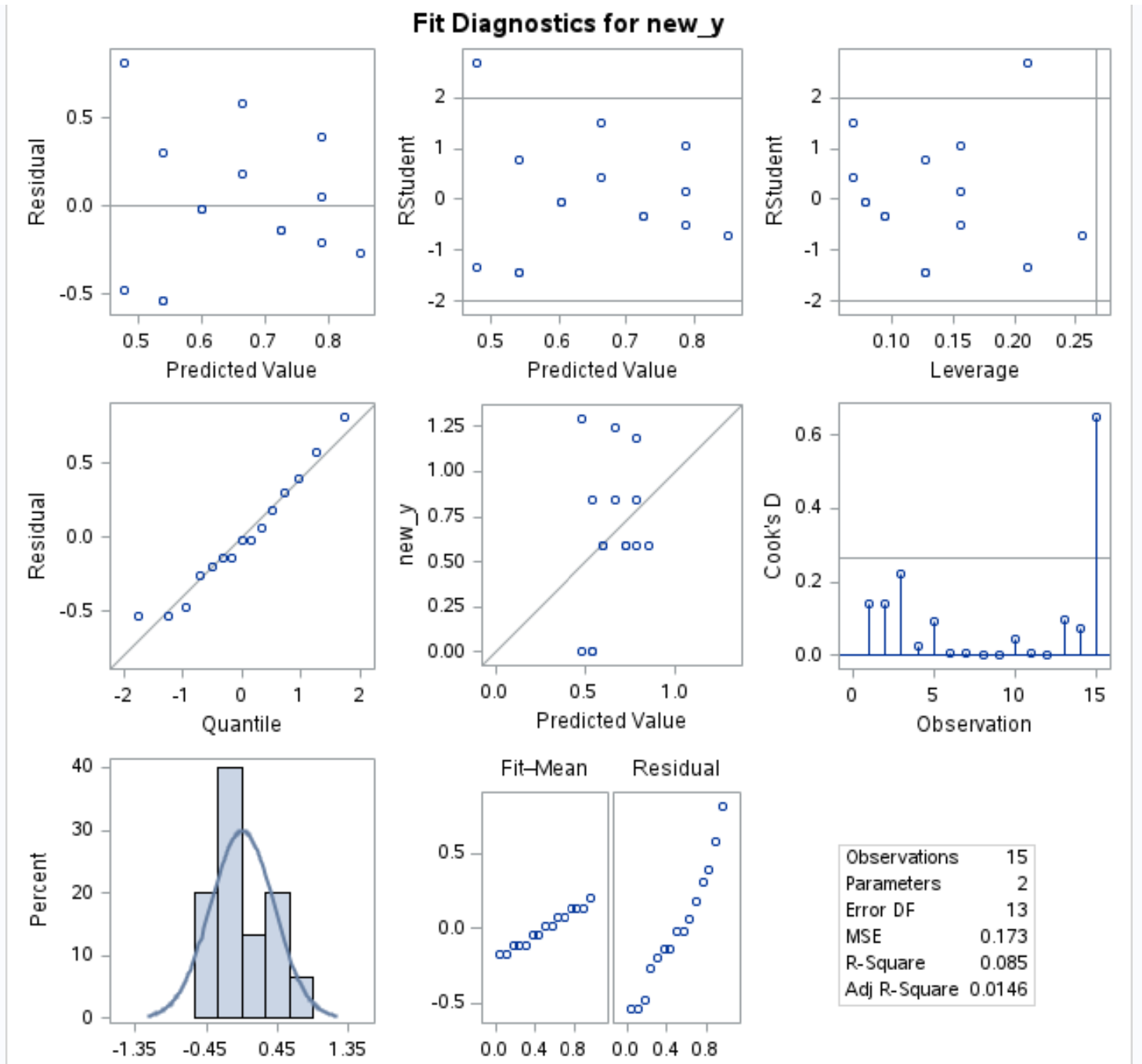
これは、ボックス-コックス変換されたモデルの残差がより正規分布しており、 線形回帰の主要な仮定の1 つを満たしていることを示しています。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。
SAS で正規性テストに Proc Univariate を使用する方法
SAS で残差プロットを作成する方法
SAS で Levene テストを実行する方法