Python で box-cox 変換を実行する方法

ボックス コックス変換は、非正規分布のデータ セットをより正規分布のセットに変換するために一般的に使用される方法です。

この方法の基本的な考え方は、次の式を使用して、変換されたデータができるだけ正規分布に近づくような λ の値を見つけることです。

• y(λ) = (y ^λ – 1) / λ (y ≠ 0 の場合)
• y = 0の場合、y(λ) = log(y)

scipy.stats.boxcox()関数を使用して、Python で box-cox 変換を実行できます。

次の例は、この関数を実際に使用する方法を示しています。

例: Python での Box-Cox 変換

指数分布から 1000 個の値のランダムなセットを生成するとします。

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

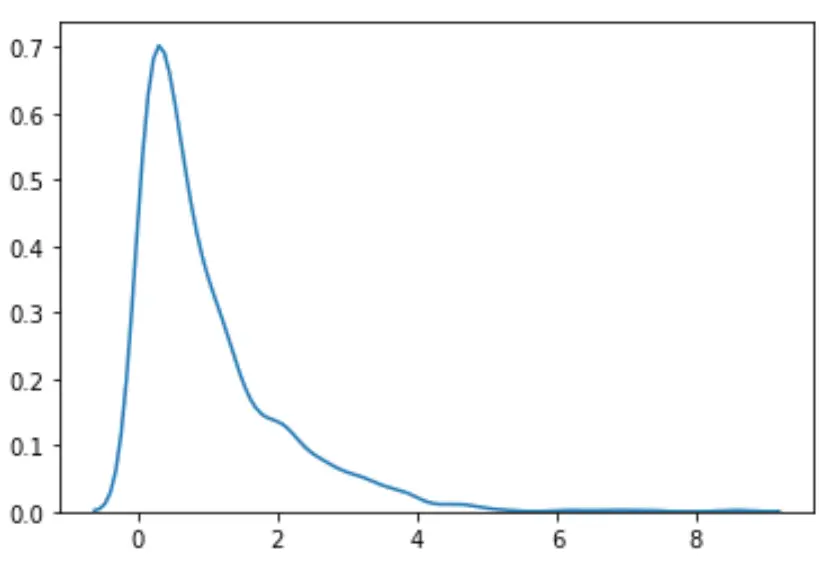
分布が正規ではないことがわかります。

boxcox()関数を使用すると、より正規分布を生成するラムダの最適値を見つけることができます。

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

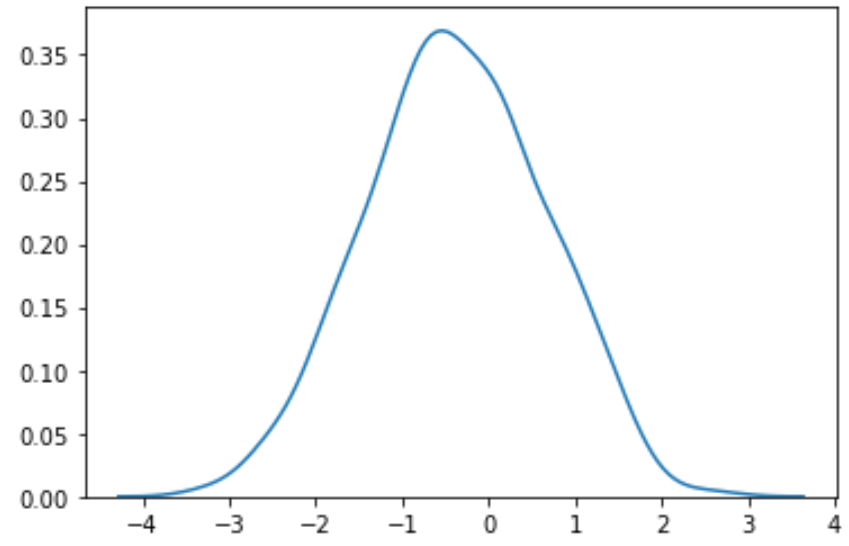
変換されたデータは、より正規分布に従っていることがわかります。

Box-Cox 変換の実行に使用される正確なラムダ値も見つけることができます。

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

最適なラムダは約0.242であることがわかりました。

したがって、各データ値は次の式を使用して変換されました。

新 = (旧^0.242 – 1) / 0.242

これは、元のデータと変換されたデータの値を確認することで確認できます。

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

元のデータセットの最初の値は0.79587でした。そこで、次の式を適用してこの値を変換しました。

新しい = (.79587 ^0.242 – 1) / 0.242 = -0.222

変換されたデータセットの最初の値が実際に-0.222であることを確認できます。

追加リソース

Python で QQ プロットを作成および解釈する方法
Python でシャピロ・ウィルク正規性テストを実行する方法