Excel でボンフェローニ補正を実行する方法

ボンフェローニ補正とは、タイプ I エラーが発生する確率を制御するために、一連の統計検定のアルファ (α) レベルを調整するプロセスを指します。

ボンフェローニ補正の公式は次のとおりです。

α_新しい= α_{オリジナル}/ n

金：

• _{オリジナル}α：オリジナルαレベル
• n: 実行された比較またはテストの合計数

たとえば、一度に 3 つの統計検定を実行し、各検定に α = 0.05 を使用したい場合、ボンフェローニ補正により、 α _new = 0.01667を使用する必要があることがわかります。

_新しいα =_元のα / n = 0.05 / 3 = 0.01667

したがって、検定の p 値が 0.01667 未満の場合にのみ、個々の検定の帰無仮説を棄却する必要があります。

このタイプの補正は、複数のグループ平均を同時に比較したい場合に、分散分析後の事後検定でよく実行されます。

次のステップバイステップの例は、Excel で一元配置分散分析の後にボンフェローニ補正を実行する方法を示しています。

ステップ 1: データを作成する

まず、試験の準備のために 3 つの異なる学習手法のいずれかを使用した学生の結果を示す偽のデータセットを作成しましょう。

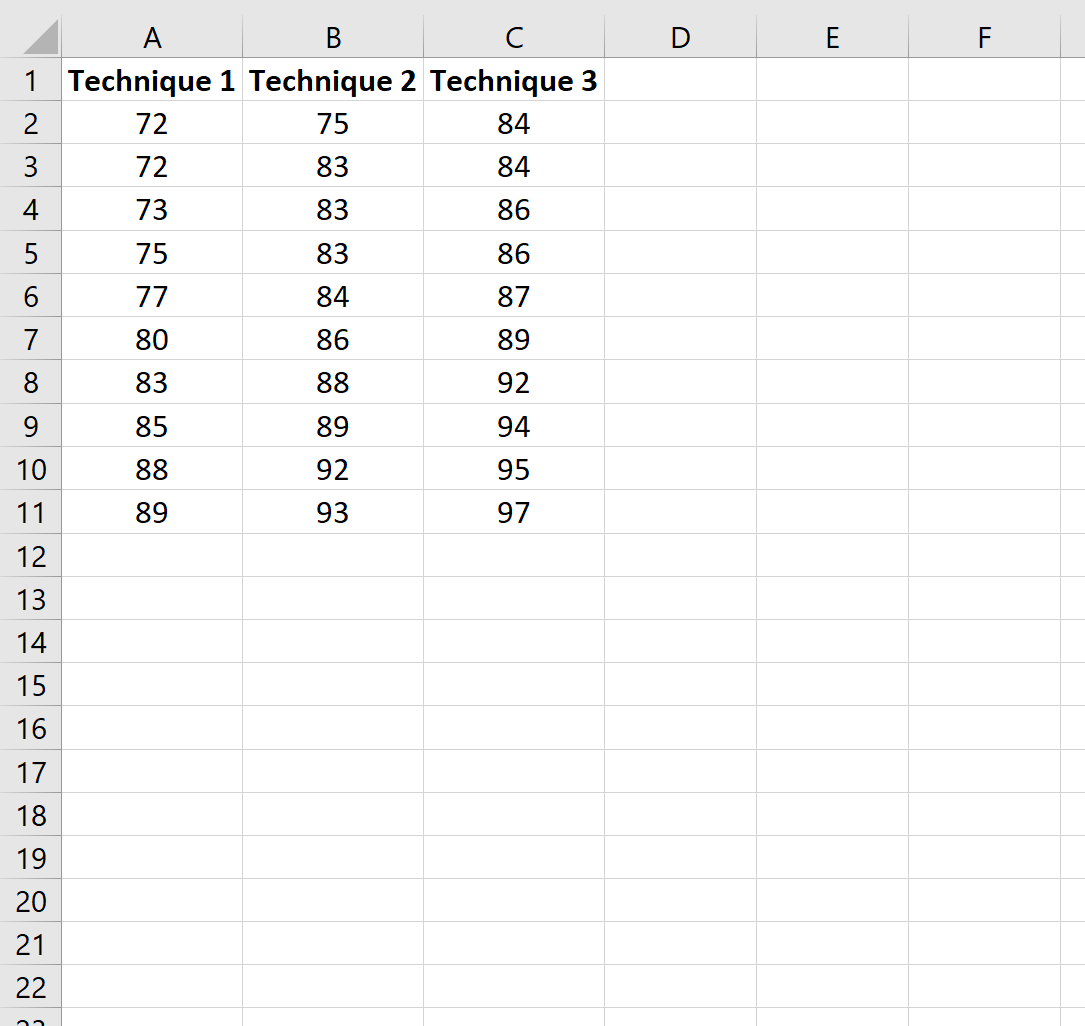
ステップ 2: 一元配置分散分析を実行する

次に、一元配置分散分析を実行して、試験の平均スコアが 3 つのグループ間で等しいかどうかを判断してみましょう。

まず、列ヘッダーを含むすべてのデータを強調表示します。

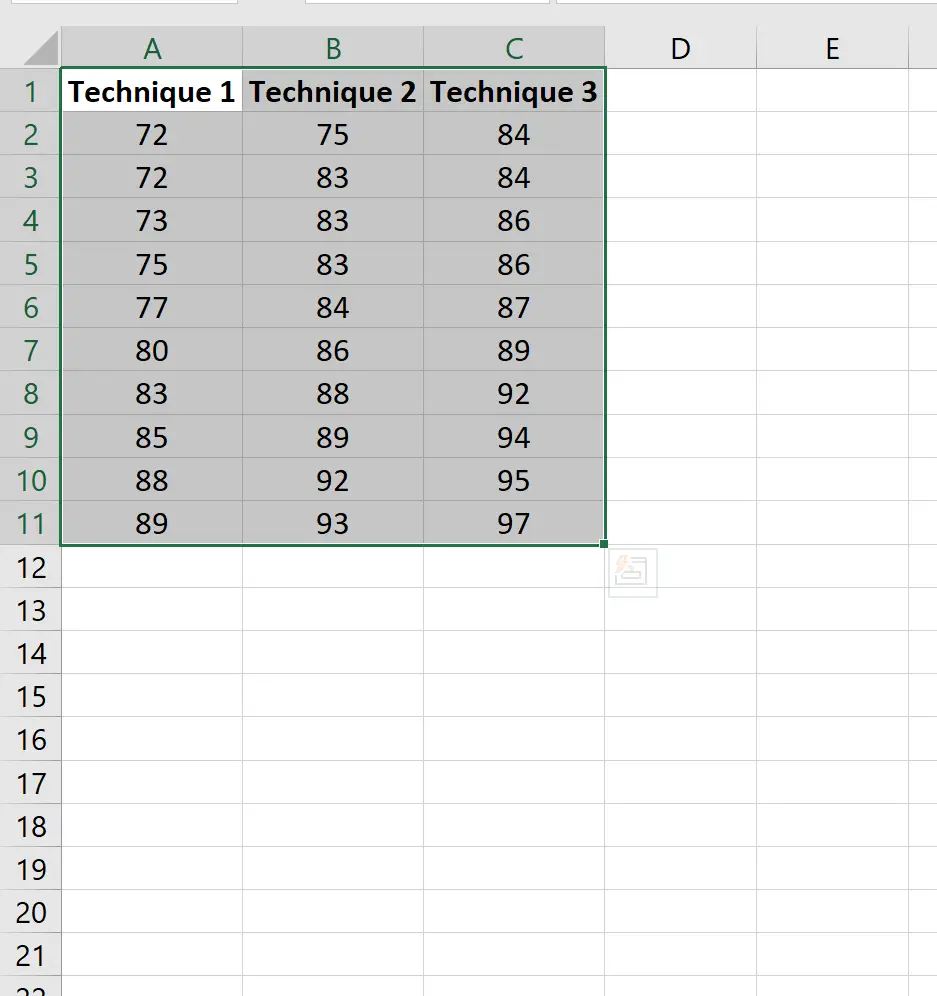
次に、上部のリボンに沿って[データ]タブをクリックし、 [データ分析] をクリックします。

このオプションが使用できない場合は、最初にAnalysis ToolPak をロードする必要があります。

表示されるウィンドウで、 「Anova: Single Factor」をクリックし、 「OK」をクリックします。

次の情報を入力し、 「OK」をクリックします。

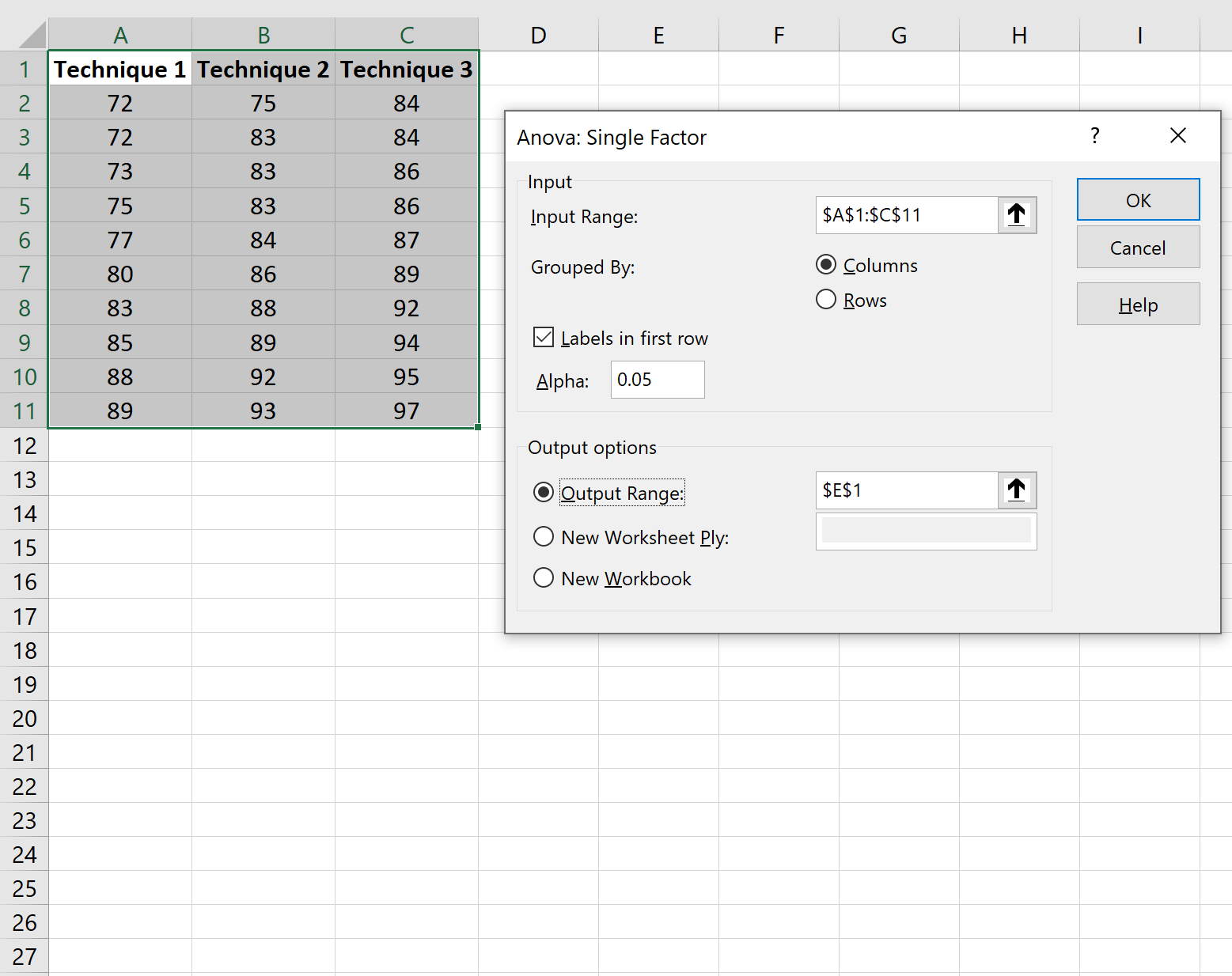
一元配置分散分析の結果が自動的に表示されます。

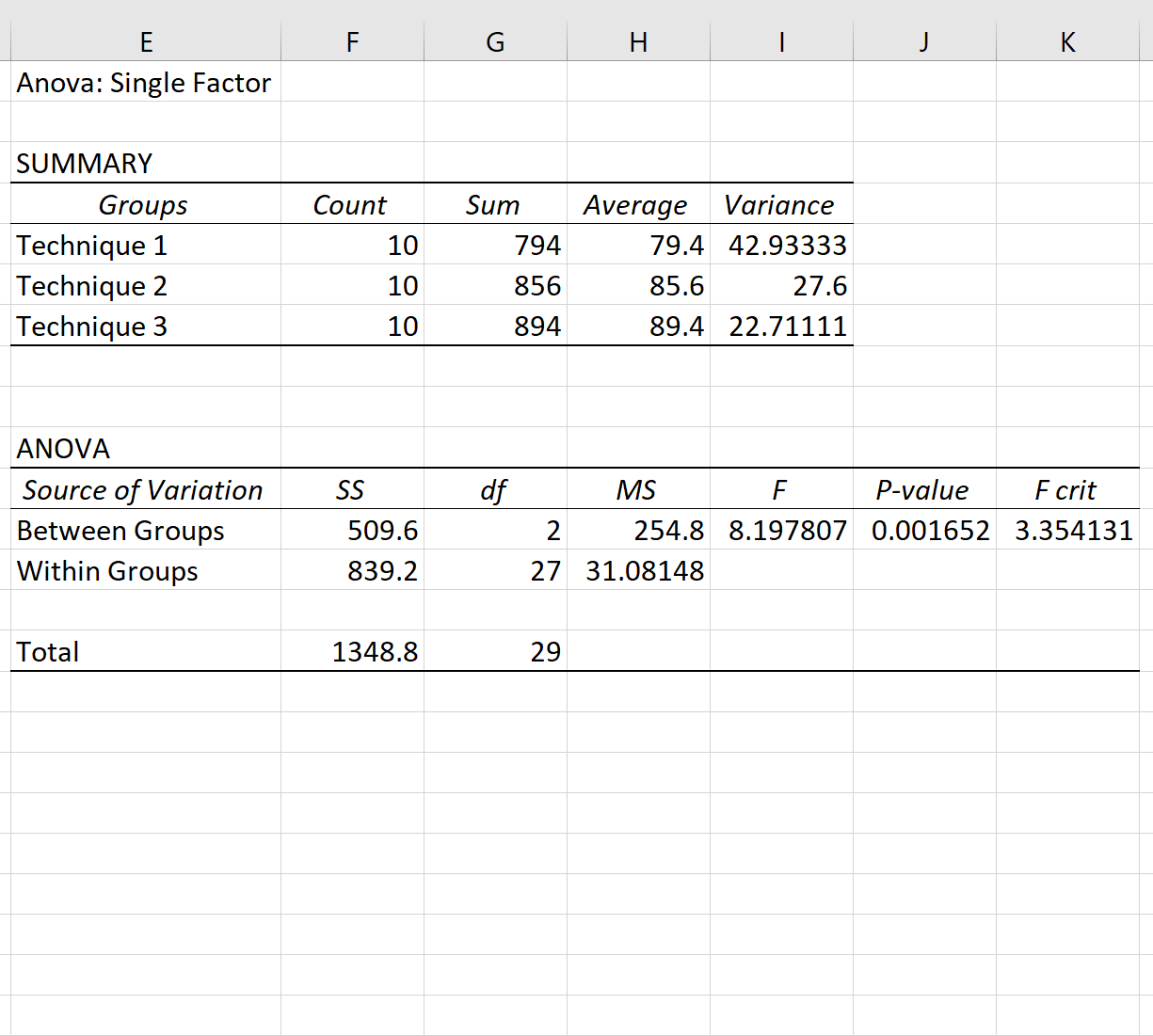
一元配置分散分析には次の帰無仮説と対立仮説があることを思い出してください。

• H ₀ (帰無仮説):すべてのグループ平均は等しい。
• H _A (対立仮説):少なくとも 1 つのグループ平均が異なる 休む。

ANOVA 表の p 値 (0.001652) は 0.05 未満であるため、帰無仮説を棄却する十分な証拠があります。言い換えれば、3 つのグループ間の試験の平均点は等しくありません。

次に、ボンフェローニ補正を使用して 3 つのグループ間でいくつかの比較を行い、どのグループの平均が異なるかを正確に確認できます。

ステップ 3: ボンフェローニ補正を使用して複数の比較を実行する

ボンフェローニ補正を使用すると、次のように調整されたアルファ レベルを計算できます。

α_新しい= α_{オリジナル}/ n

この例では、次の 3 つの比較を実行します。

• テクニック 1 とテクニック 2
• テクニック 1 とテクニック 3
• テクニック 2 とテクニック 3

各テストで α = .05 を使用したいため、ボンフェローニ補正により、 α _new = .0167を使用する必要があることがわかります。

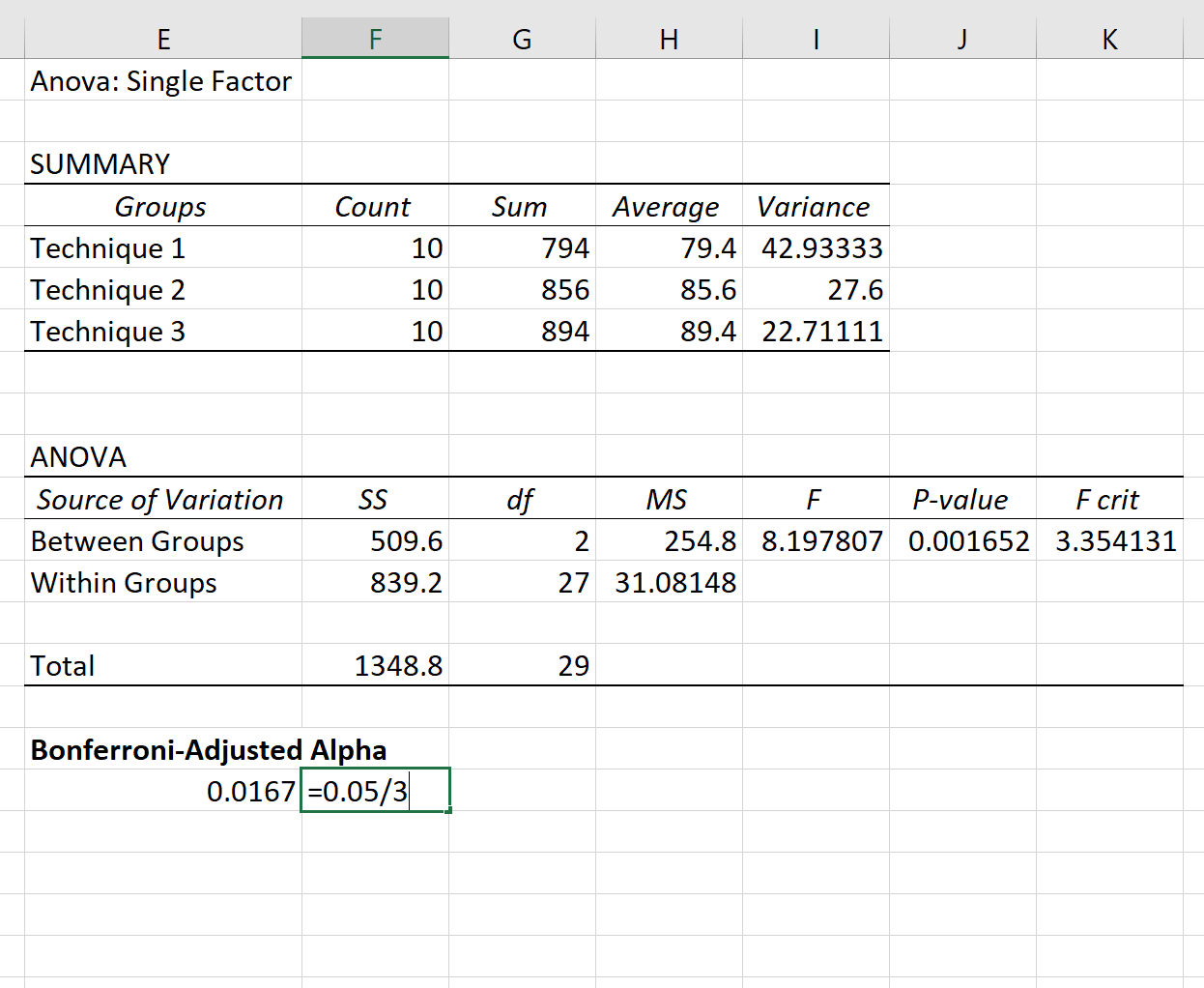
次に、t 検定を使用して各グループ間の平均を比較します。 Excel では、次の構文を使用できます。

=TTEST(テーブル1、テーブル2、キュー=2、タイプ=2)

金：

• Array1:最初のデータ配列
• Array2: 2 番目のデータ配列
• 尾:テストの尾の数。両側検定を示すには「2」を使用します。
• type:実行する t 検定のタイプ。等分散の t 検定を示すには「2」を使用します。

次のスクリーンショットは、各 t 検定の実行方法を示しています。

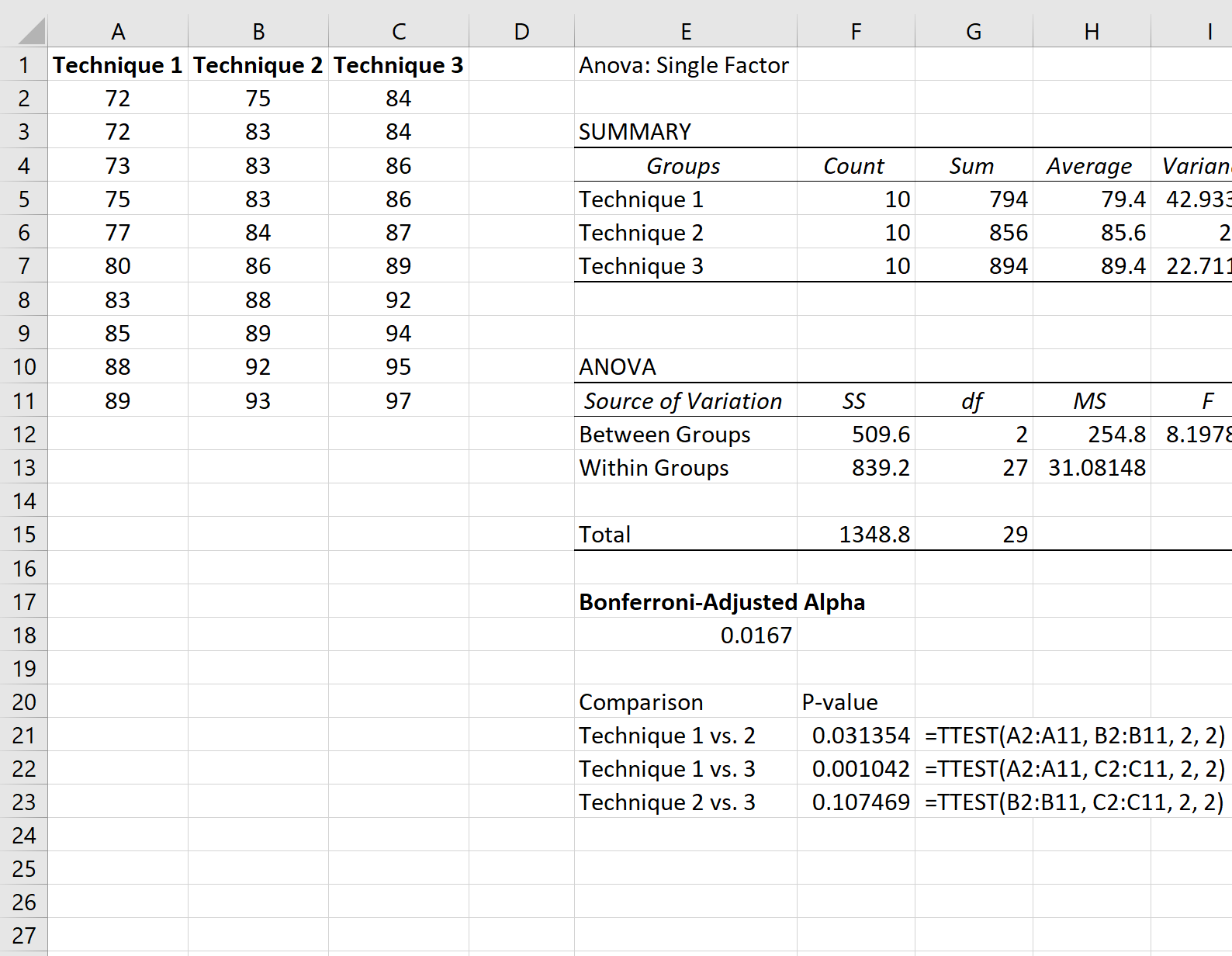
ボンフェローニ調整アルファ レベルを下回る唯一の p 値は、テクニック 1 とテクニック 2 の比較から得られ、p 値は0.001042でした。

したがって、平均試験スコアにおける統計的に有意な差はテクニック 1 とテクニック 2 の間のみであると結論付けることができます。

追加リソース

家族ごとのエラー率はどれくらいですか?
ボンフェローニ補正: 定義と例
ボンフェローニ補正計算機