Stata で manova を実行する方法
一元配置分散分析は、説明変数の異なる水準が特定の応答変数において統計的に異なる結果をもたらすかどうかを判断するために使用されます。
たとえば、3 つの教育レベル (準学士号、学士号、修士号) が統計的に異なる年収につながるかどうかを理解することに興味があるかもしれません。この場合、説明変数と応答変数があります。
- 説明変数:教育レベル
- 応答変数:年収
MANOVA は、複数の応答変数がある一元配置分散分析を拡張したものです。たとえば、教育レベルによって年収や学生ローンの額が異なるかどうかを理解することに興味があるかもしれません。この場合、1 つの説明変数と 2 つの応答変数があります。
- 説明変数:教育レベル
- 応答変数:年収、学生ローン
複数の応答変数があるため、この場合は MANOVA を使用するのが適切です。
次に、Stata で MANOVA を実行する方法を説明します。
例: Stata の MANOVA
Stata で MANOVA を実行する方法を説明するために、24 人に対する次の 3 つの変数を含む次のデータセットを使用します。
- educ:学習レベル (0 = アソシエイト、1 = 学士、2 = 修士)
- 収入:年収
- 負債:学生ローンの負債総額
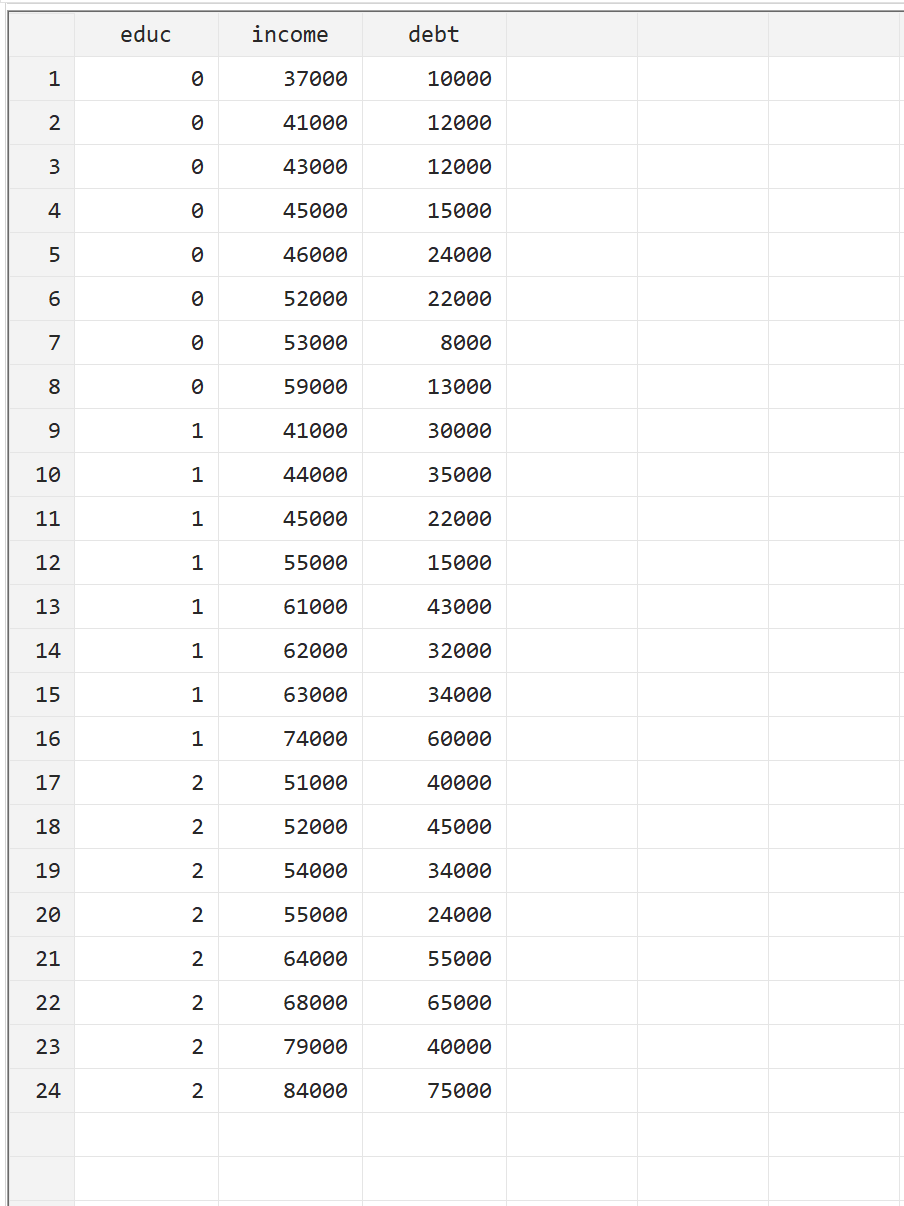
この例は、上部のメニュー バーで[データ] > [データ エディター] > [データ エディター (編集)]に移動し、手動でデータを入力することで再現できます。
教育を説明変数として、収入と負債を応答変数として使用して MANOVA を実行するには、次のコマンドを使用できます。
所得負債マノバ = 教育

Stata は、4 つの固有の検定統計量とそれらに対応する p 値を生成します。
ウィルクスのラムダ: F 統計量 = 5.02、P 値 = 0.0023。
Pillai トレース: F 統計量 = 4.07、P 値 = 0.0071。
Lawley-Hotelling トレース: F 統計量 = 5.94、P 値 = 0.0008。
最大のロイ根: F 統計 = 13.10、P 値 = 0.0002。
各テスト統計の計算方法の詳細については、ペンシルベニア州立エバリー科学大学のこの記事を参照してください。
各検定統計量の p 値は 0.05 未満であるため、どの検定統計量を使用しても帰無仮説は棄却されます。これは、教育レベルによって年収と学生負債総額に統計的に有意な差が生じると言える十分な証拠があることを意味します。
p 値に関する注意:出力テーブルの p 値の横にある文字は、F 統計量がどのように計算されたかを示します (e = 正確な計算、a = 近似計算、u = 上限)。