完全ガイド: manova の仮定を確認する方法

によるベンジャミン・アンダーソン博士 7月 24, 2023 ガイド 0コメント

MANOVA (多変量分散分析) は、1 つ以上の因子変数が複数の応答変数にどのような影響を与えるかを分析するために使用されます。

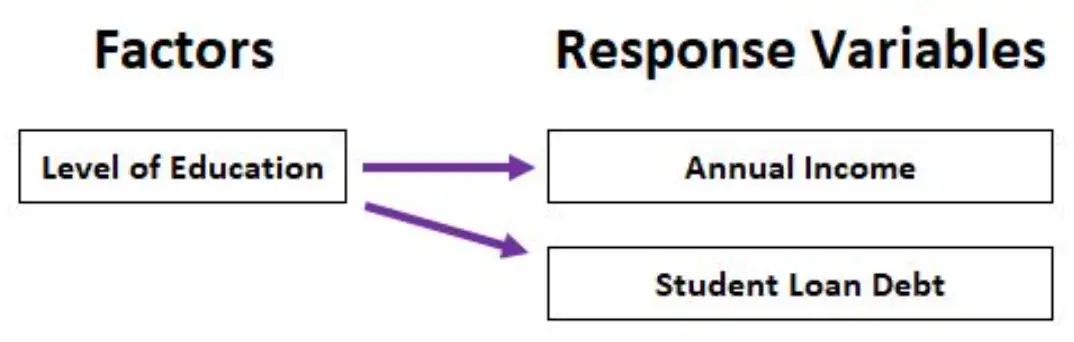
たとえば、MANOVA を使用して、教育レベル (高校卒業資格、準学士号、学士号、修士号) が年収と学生ローン総負債の両方にどのような影響を与えるかを分析できます。

関連: ANOVA、ANCOVA、MANOVA、MANCOVA の違い

MANOVA を実行するたびに、次の前提条件が満たされていることを確認する必要があります。

1. 多変量正規性– 応答変数は、因子変数の各グループ内で多変量正規分布します。

2. 独立性– 各観測値は母集団からランダムかつ独立してサンプリングされます。

3. 等分散– 各グループの母集団共分散行列は等しい。

4. 多変量外れ値がない– 極端な多変量外れ値はありません。

この記事では、各仮定の説明と、その仮定が満たされているかどうかを判断する方法を説明します。

MANOVA は、応答変数が因子変数の各グループ内で多変量正規分布すると仮定します。

各因子 * 応答変数の組み合わせに少なくとも 20 個の観測値がある場合、多変量正規性の仮定が満たされていると仮定できます。

各因子 * 応答変数の組み合わせの観測値が 20 未満の場合は、散布図行列を作成して残差を視覚化し、この仮定が満たされているかどうかを視覚的に確認できます。

幸いなことに、MANOVA は多変量正規性からの逸脱に対して頑強であることがよく知られているため、小さいから中程度の逸脱は通常は問題になりません。

MANOVA は、各観測値が母集団からランダムかつ独立してサンプリングされることを前提としています。

データの収集に確率サンプリング法(母集団の各メンバーがサンプルに含まれるように選択される確率が等しい) が使用されている限り、各観測値はランダムかつ独立した方法でサンプリングされたと想定できます。

確率サンプリング手法の例は次のとおりです。

MANOVA は、各グループの母集団共分散行列が等しいと仮定します。

この仮説を検証する最も一般的な方法は、Box の M 検定を使用することです。この検定は非常に厳密であることが知られているため、母集団の共分散行列が等しいかどうかを判断するために通常は有意水準 0.001 が使用されます。

Box の M 検定の p 値が 0.001 より大きい場合、この仮定が満たされていると考えることができます。

幸いなことに、たとえ検定の p 値が 0.001 未満であっても、MANOVA はこの仮説からの逸脱に対して頑健である傾向があります。

等しくない共分散行列が問題になるには、共分散行列間の差異が非常に極端である必要があります。

MANOVA は、結果に大きな影響を与える可能性のある極端な多変量外れ値がデータ内に存在しないことを前提としています。

この仮定を検証する最も一般的な方法は、各観測値のマハラノビス距離を計算することです。これは、多変量空間内の 2 点間の距離を表します。

観測値のマハラノビス距離に対応する p 値が 0.001 未満の場合、通常、その観測値は極端な外れ値であると宣言されます。

さまざまな統計ソフトウェアでマハラノビス距離を計算する方法については、次のチュートリアルを参照してください。

次のチュートリアルでは、さまざまな統計ソフトウェアで MANOVA を実行する方法を説明します。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る