Spss でマン-ホイットニー u 検定を実行する方法
マン-ホイットニー U 検定(ウィルコクソン順位和検定とも呼ばれます) は、標本分布が正規分布しておらず、標本サイズが小さい (n < 30) 場合に、2 つの標本間の差異を比較するために使用されます。これは、2 サンプル t 検定と同等のノンパラメトリックとみなされます。
このチュートリアルでは、SPSS でマン-ホイットニー U 検定を実行する方法について説明します。
例: SPSS でのマン-ホイットニー U 検定
研究者らは、燃料処理によって車の平均燃費が変化するかどうかを知りたいと考えています。これをテストするために、燃料処理を行った 12 台の車と処理を行わなかった 12 台の車の燃費を測定する実験を実施しました。
次のスクリーンショットは、各車の mpg とそれが属するグループを示しています (0 = 燃料処理なし、1 = 燃料処理)。
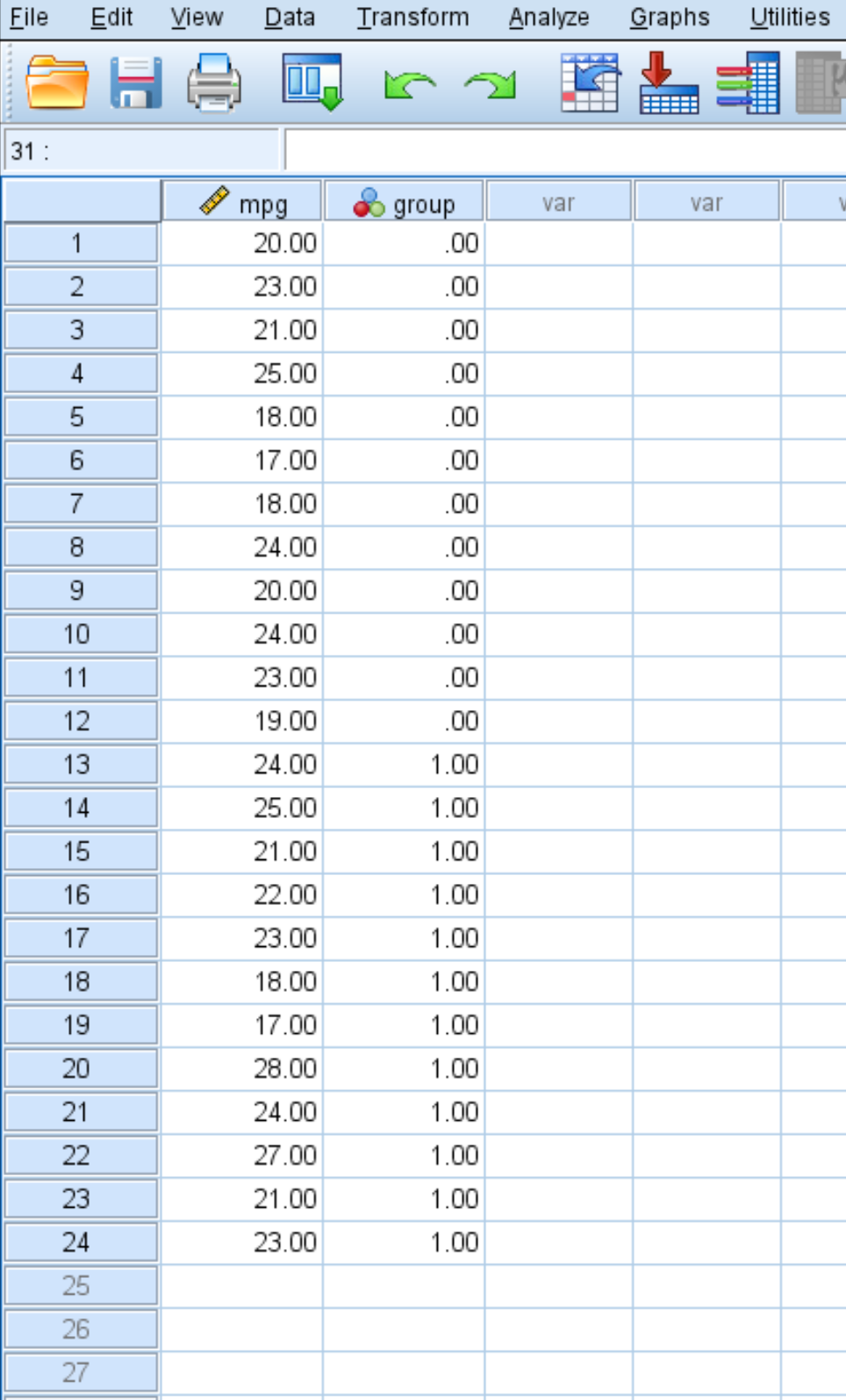
サンプルサイズが小さく、研究者らはサンプル分布が正規分布ではないのではないかと疑ったため、マン・ホイットニーの U 検定を実行して、2 つのグループ間に mpg に統計的に有意な差があるかどうかを判断することにしました。
SPSS でマン-ホイットニー U 検定を実行するには、次の手順を実行します。
ステップ 1: Mann-Whitney U テスト オプションを選択します。
[分析]タブ、 [ノンパラメトリック テスト] 、 [レガシー ダイアログ] 、 [2 つの独立したサンプル] の順にクリックします。
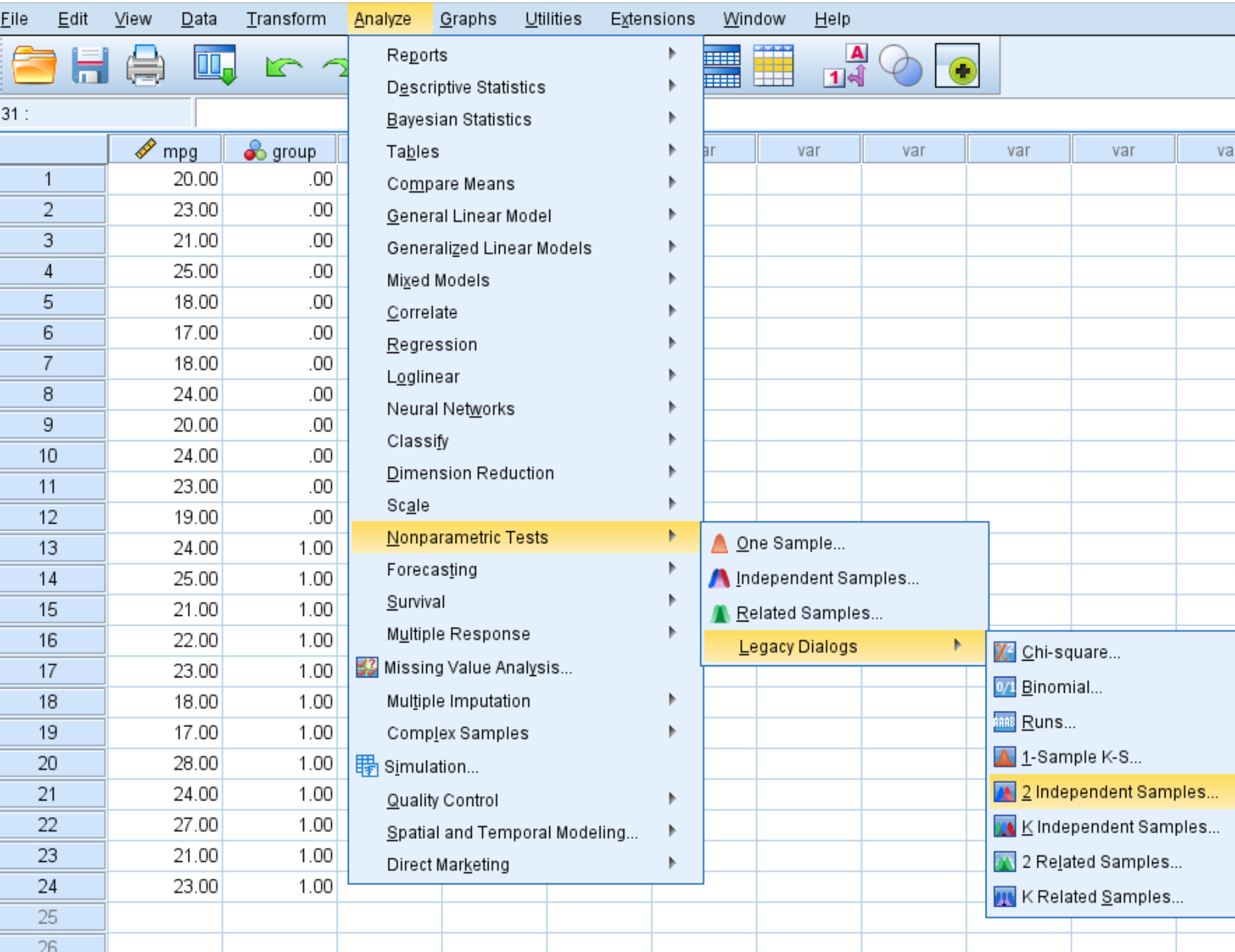
ステップ 2: テストを実行するために必要な値を入力します。
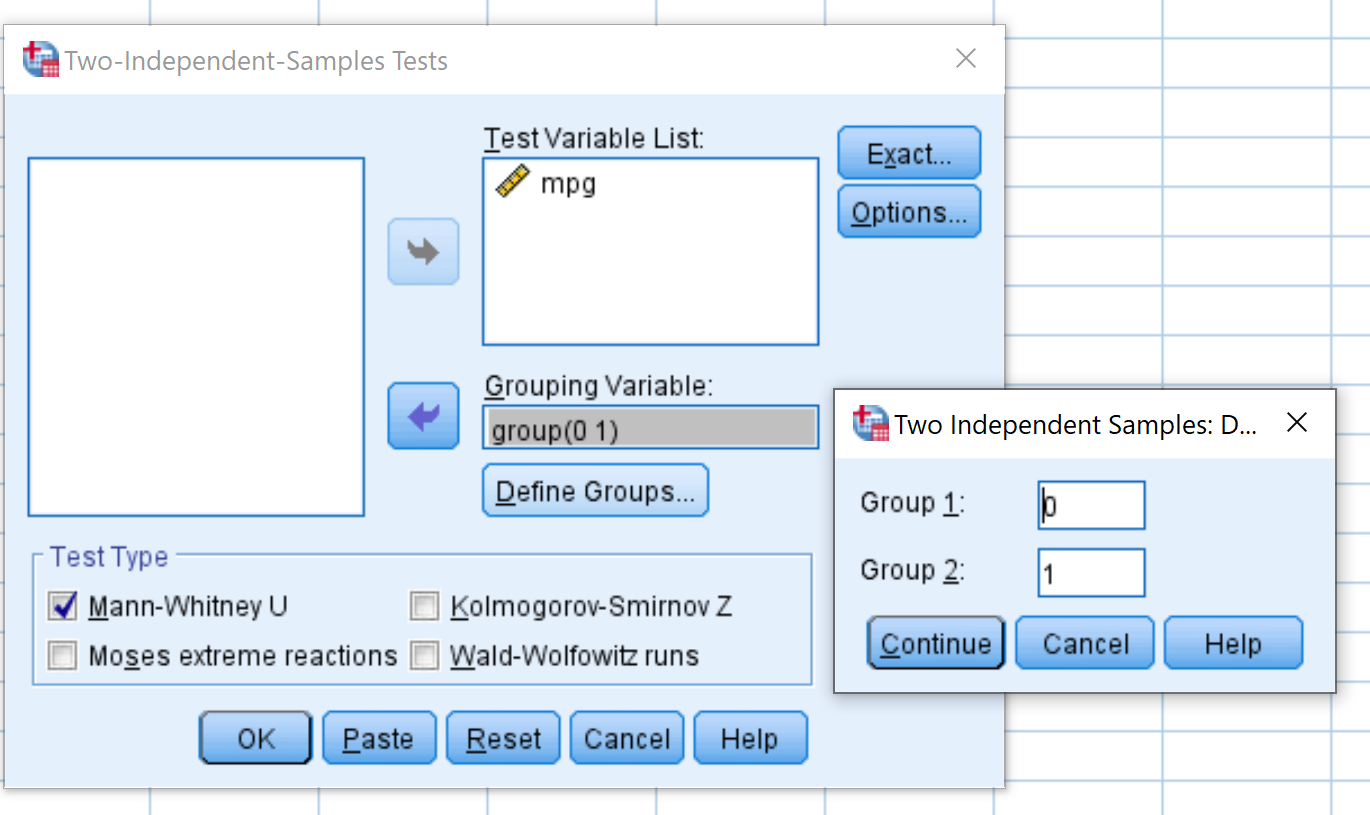
mpg を「テスト変数リスト」というラベルの付いた領域にドラッグし、それを「グループ化変数」というラベルの付いた領域にグループ化します。 「グループの定義」をクリックし、グループ 1 を値 0 の行として定義し、グループ 2 を値 1 の行として定義します。
Mann-Whitney Uの横のボックスがオンになっていることを確認します。次に、 「OK」をクリックします。
ステップ 3: 結果を解釈します。
[OK]をクリックすると、Mann-Whitney U テストの結果が表示されます。
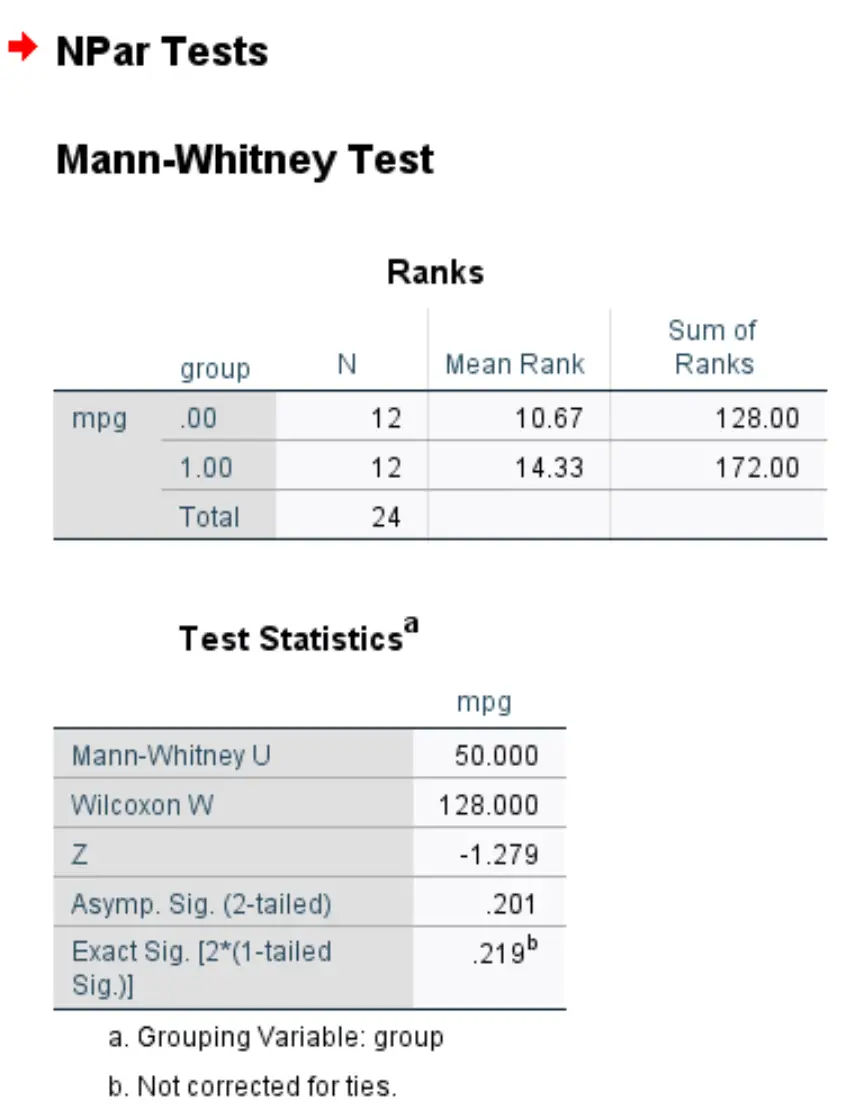
結果の最も重要な数値は、 Z 検定統計量と両側漸近p値です。
- Z 検定統計量: -1.279
- p値: 0.201
p 値は 0.05 未満ではないため、帰無仮説を棄却できません。真の平均mpgが2つのグループ間で異なると言える十分な証拠はありません。
ステップ 4: 結果を報告します。
最後に、Mann-Whitney U 検定の結果を報告します。これを行う方法の例を次に示します。
マン・ホイットニー U テストは、新しい燃料処理によってガロンあたりの平均マイル数に違いが生じるかどうかを判断するために、24 台の車に対して実行されました。各グループには12台の車がありました。
結果は、平均 mpg が 2 つのグループ間で統計的に差がなく (z = -1.279、p = 0.2010)、有意水準 0.05 であることを示しました。
これらの結果に基づくと、新しい燃料処理は自動車のガロンあたりの走行距離に大きな影響を与えません。