マン・ホイットニーの u 検定
マン-ホイットニー U 検定(ウィルコクソン順位和検定とも呼ばれます) は、標本分布が正規分布しておらず、標本サイズが小さい (n < 30) 場合に、2 つの独立した標本間の差異を比較するために使用されます。
これは、独立した 2 サンプルの t 検定とノンパラメトリックな同等であると考えられます。
Mann-Whitney U 検定を使用できる例をいくつか示します。
- 大学 A の卒業生 5 人の給与と大学 B の卒業生 5 人の給与を比較したいとします。給与は正規分布ではありません。
- 食事 A を使用した 12 名と食事 B を使用した 10 名の 2 つのグループで体重減少が異なるかどうかを知りたいとします。体重減少は正規分布しません。
- クラス A の 8 人の生徒のスコアがクラス B の 7 人の生徒のスコアと異なるかどうかを知りたいとします。スコアは正規分布しません。
各例では、標本分布が正規分布ではなく、標本サイズが小さい 2 つのグループを比較します。
したがって、次の仮定が満たされる限り、マン-ホイットニー U 検定は適切です。
マン・ホイットニーの U 検定の仮定
マン-ホイットニー U 検定を実行する前に、次の 4 つの前提条件が満たされていることを確認する必要があります。
- 順序または連続:分析している変数は順序または連続です。順序変数の例には、リッカート項目 (たとえば、「まったく同意しない」から「非常に同意する」までの範囲の 5 段階評価) が含まれます。連続変数の例には、身長 (インチで測定)、体重 (ポンドで測定)、またはテストのスコア (0 から 100 で測定) が含まれます。
- 独立性:両方のグループからのすべての観測値は互いに独立しています。
- 形状: 2 つのグループの分布の形状はほぼ同じです。
これらの仮定が満たされている場合は、マン-ホイットニー U 検定を実行できます。
マン・ホイットニー U 検定の実行方法
マン-ホイットニー U 検定を実行するには、標準的な 5 段階の仮説検定手順に従います。
1. 仮定を述べます。
ほとんどの場合、マン-ホイットニー U 検定は両側検定として実行されます。帰無仮説と対立仮説は次の形式で記述されます。
H 0 : 2 つの母集団は等しい
H a : 2 つの母集団は等しくありません
2. 仮説に使用する有意水準を決定します。
重要度のレベルを決定します。一般的な選択肢は .01、.05、および .1 です。
3. 検定統計量を見つけます。
検定統計量は U で示され、以下に定義されているように、U 1と U 2の小さい方です。
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
ここで、n 1と n 2 はそれぞれサンプル 1 と 2 のサンプル サイズであり、R 1と R 2はそれぞれサンプル 1 と 2 のランクの合計です。
以下の例では、この検定統計量を見つける方法を詳しく示します。
4. 帰無仮説を棄却するか、棄却しません。
検定統計量を使用して、Mann-Whitney U 表で見つかった有意水準と臨界値に基づいて帰無仮説を棄却できるかどうかを判断します。
5. 結果を解釈します。
質問された内容に基づいてテスト結果を解釈します。
マン・ホイットニー U 検定の実行例
次の例は、マン-ホイットニー U 検定を実行する方法を示しています。
例1
私たちは、新しい薬がパニック発作の予防に効果があるかどうかを知りたいと考えています。合計 12 人の患者がランダムに 6 人ずつ 2 つのグループに分けられ、新薬またはプラセボの投与に割り当てられます。次に、患者は 1 か月間で経験したパニック発作の回数を記録します。
結果を以下に示します。
| 新薬 | プラセボ |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
マン-ホイットニー U 検定を実行して、新薬群と比較してプラセボ群の患者のパニック発作の数に違いがあるかどうかを確認します。有意水準 0.05 を使用します。
1. 仮定を述べます。
H 0 : 2 つの母集団は等しい
H a : 2 つの母集団は等しくありません
2. 仮説に使用する有意水準を決定します。
この問題は、有意水準 0.05 を使用する必要があることを示しています。
3. 検定統計量を見つけます。
検定統計量は U で示され、以下に定義されているように U 1と U 2の小さい方であることを思い出してください。
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
ここで、n 1と n 2 はそれぞれサンプル 1 と 2 のサンプル サイズであり、R 1と R 2はそれぞれサンプル 1 と 2 のランクの合計です。
R 1 と R 2を見つけるには、両方のグループの観測値を組み合わせて、最小値から最大値の順に並べる必要があります。
| 新薬 | プラセボ |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
合計サンプル: 1 、 1 、 2 、 3 、 3 、 4 、 4 、 5 、 5 、 6 、 8 、 9
ランク: 1.5 、 1.5 、 3 、 4.5 、 4.5 、 6.5 、 6.5 、 8.5 、 8.5 、 10 、 11 、 12
R 1 = サンプル 1 のランクの合計 = 1.5+4.5+4.5+6.5+8.5+8.5 = 34
R 2 = サンプル 2 のランクの合計 = 1.5+3+6.5+10+11+12 = 44
次に、サンプル サイズ n 1と n 2 、およびランク合計 R 1と R 2を使用して、U 1と U 2を見つけます。
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
テスト統計はU1とU2の小さい方で、たまたま U=13 です。
注: Mann-Whitney U 検定計算機を使用して、U = 13 であることを確認することもできます。
4. 帰無仮説を棄却するか、棄却しません。
n 1 = 6 および n 2 = 6 を有意水準 0.05 として使用すると、マン-ホイットニー U 表から臨界値は 5 であることが分かります。
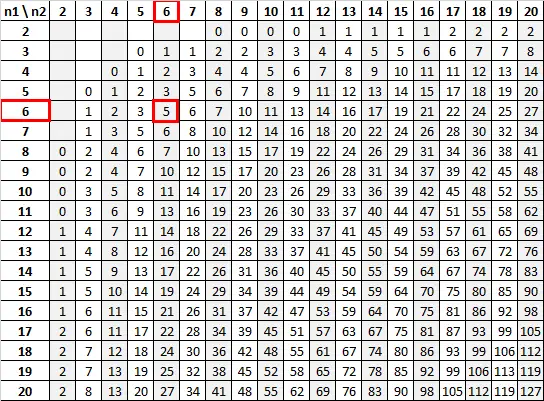
検定統計量 (13) が臨界値 (5) より大きいため、帰無仮説を棄却できません。
5. 結果を解釈します。
帰無仮説を棄却できなかったため、プラセボ群の患者が経験したパニック発作の回数が新薬群の患者と異なると言える十分な証拠はありません。
例 2
私たちは、1 週間 1 日 30 分の勉強が生徒のテストの成績向上に役立つかどうかを知りたいと考えています。合計 15 人の患者が研究グループまたは研究グループに無作為に割り当てられます。 1週間後、生徒全員が同じテストを受けます。
両方のグループのテスト結果を以下に示します。
| 勉強 | 勉強しない |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
マン-ホイットニー U 検定を実行して、研究グループと研究グループのテストスコアに違いがあるかどうかを確認します。有意水準 0.01 を使用します。
1. 仮定を述べます。
H 0 : 2 つの母集団は等しい
H a : 2 つの母集団は等しくありません
2. 仮説に使用する有意水準を決定します。
この問題は、有意水準 0.01 を使用する必要があることを示しています。
3. 検定統計量を見つけます。
検定統計量は U で示され、以下に定義されているように U 1と U 2の小さい方であることを思い出してください。
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
ここで、n 1と n 2 はそれぞれサンプル 1 と 2 のサンプル サイズであり、R 1と R 2はそれぞれサンプル 1 と 2 のランクの合計です。
R 1 と R 2を見つけるには、両方のグループの観測値を組み合わせて、最小値から最大値の順に並べる必要があります。
| 勉強 | 勉強しない |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
合計サンプル: 72 、 75 、 80 、 81 、 84 、 88 、 89 、 90 、 91 、 92 、 93 、 94 、 95 、 96 、 99
行: 1 、 2 、 3 、 4 、 5 、 6 、 7 、 8 、 9 、 10 、 11 、 12 、 13 、 14 、 15
R 1 = サンプル 1 のランクの合計 = 5+7+8+9+10+12+14+15 = 80
R 2 = サンプル 2 のランクの合計 = 1+2+3+4+6+11+13 = 40
次に、サンプル サイズ n 1と n 2 、およびランク合計 R 1と R 2を使用して、U 1と U 2を見つけます。
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
テスト統計はU1とU2の小さい方で、たまたま U=12 です。
注: Mann-Whitney U 検定計算機を使用して、U = 12 であることを確認することもできます。
4. 帰無仮説を棄却するか、棄却しません。
有意水準 0.01 で n 1 = 8 および n 2 = 7 を使用すると、Mann-Whitney U 表から臨界値は 6 であることが分かります。
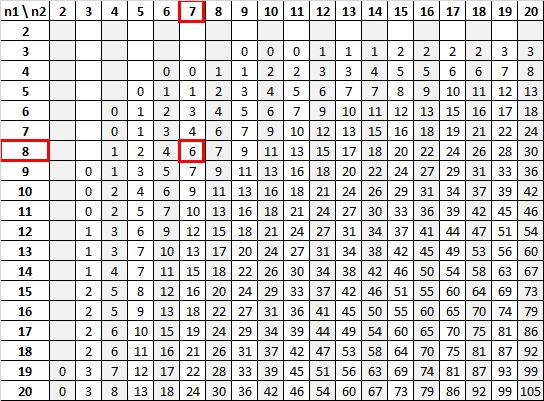
検定統計量 (12) が臨界値 (6) より大きいため、帰無仮説を棄却できません。
5. 結果を解釈します。
帰無仮説を棄却できなかったため、勉強した生徒のテストのスコアが勉強しなかった生徒のテストのスコアと異なると言える十分な証拠はありません。
追加リソース
マン・ホイットニーの U 検定計算機
マン・ホイットニー U テーブル
Excel でマン-ホイットニー U 検定を実行する方法
R でマン-ホイットニー U 検定を実行する方法
Python で Mann-Whitney U 検定を実行する方法
SPSS でマン-ホイットニー U 検定を実行する方法
Stata でマン-ホイットニー U 検定を実行する方法