メイvs. rmse: どの指標を使用する必要がありますか?
回帰モデルは、1 つ以上の予測変数と応答変数の間の関係を定量化するために使用されます。
回帰モデルを当てはめるときは常に、モデルが予測変数の値をどの程度うまく使用して応答変数の値を予測できるかを理解したいと考えます。
モデルがデータセットにどの程度適合しているかを定量化するためによく使用される 2 つの指標は、平均絶対誤差 (MAE) と二乗平均平方根誤差 (RMSE) です。これらは次のように計算されます。
MAE : データセット内の予測値と実際の値の間の平均絶対差を示す指標。 MAE が低いほど、モデルはデータセットに適合します。
MAE = 1/n * Σ|y i – ŷ i |
金:
- Σは「和」を意味する記号です
- y iはi 番目の観測値の観測値です
- ŷ iは i番目の観測値の予測値です
- n はサンプルサイズです
RMSE : データセット内の予測値と実際の値の間の二乗平均平方根の差の平方根を示す指標。 RMSE が低いほど、モデルはデータセットに適合します。
次のように計算されます。
RMSE = √ Σ(y i – ŷ i ) 2 / n
金:
- Σは「和」を意味する記号です
- ŷ iは i番目の観測値の予測値です
- y iはi 番目の観測値の観測値です
- n はサンプルサイズです
例: RMSE と MAE の計算
回帰モデルを使用して、バスケットボールの試合で 10 人の選手が何点を獲得するかを予測するとします。
次の表は、モデルによって予測されたポイントとプレーヤーが獲得した実際のポイントを比較したものです。

MAE 計算ツールを使用すると、MAE が3.2 であることが計算できます。
これは、モデルによって予測された値と実際の値の間の平均絶対差が 3.2 であることを示しています。
RMSE 計算ツールを使用すると、RMSE が4に等しいことが計算できます。
これにより、予測得点と実際の得点の差の二乗平均平方根の平方根が 4 であることがわかります。
各メトリクスは、モデルによって作成された予測値とデータセット内の実際の値の間の一般的な違いを示しますが、各メトリクスの解釈は若干異なることに注意してください。
RMSE と MAE: どちらの指標を使用する必要がありますか?
平均から離れている観測値により多くの重みを割り当てたい場合 (つまり、偏差 20 が偏差 10 の 2 倍以上悪い場合)、誤差の測定に RMSE を使用する方が良いです。平均値から離れた観測値に対してより敏感になります。
ただし、20 で「オフセット」されることが 10 で「オフセット」されるよりも 2 倍悪い場合は、MAE を使用する方が良いでしょう。
これを説明するために、得点数の点で明らかに異常値であるプレーヤーがいると仮定します。
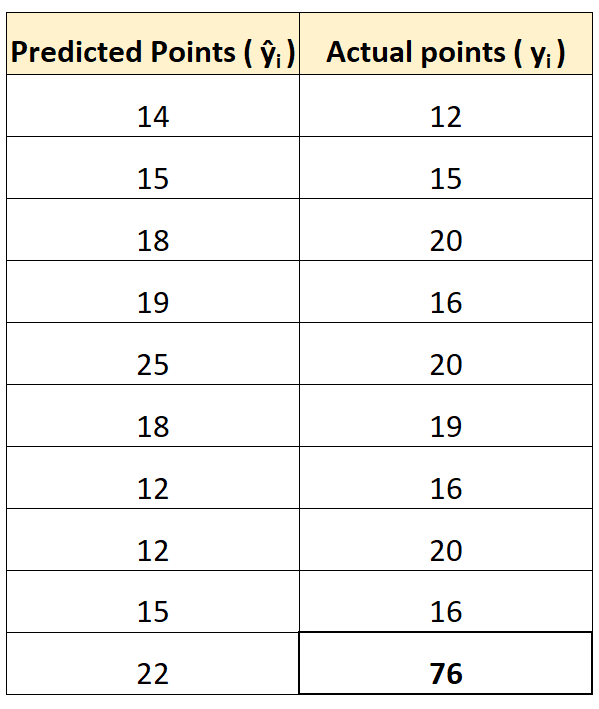
前述のオンライン計算ツールを使用すると、MAE と RMSE を次のように計算できます。
- 前:8
- RMSE : 16.4356
RMSE は MAE よりも大幅に増加することに注意してください。
これは、RMSE が計算式で差の二乗を使用しており、観測値 76 と予測値 22 の間の二乗差が非常に大きいためです。これにより、RMSE 値が大幅に増加します。
実際には、通常、複数の回帰モデルをデータセットに適合させ、モデルごとにこれらの指標のうち 1 つだけを計算します。
たとえば、3 つの異なる回帰モデルを当てはめて、各モデルの RMSE を計算できます。次に、RMSE 値が最も低いモデルを「最良の」モデルとして選択します。これは、データセット内の実際の値に最も近い予測を行うモデルだからです。
いずれの場合も、モデルごとに同じメトリックを計算するようにしてください。たとえば、あるモデルの MAE と別のモデルの RMSE を計算して、これら 2 つの測定値を比較しないでください。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアを使用して MAE を計算する方法を説明します。
Excelで平均絶対誤差を計算する方法
R の平均絶対誤差を計算する方法
Python で平均絶対誤差を計算する方法
次のチュートリアルでは、さまざまな統計ソフトウェアを使用して RMSE を計算する方法を説明します。