モランの自己とは何ですか? (定義&例)
Moran の I は、空間的自己相関を測定する方法です。
簡単に言えば、2D 空間内で値がどの程度密集しているかを定量化する方法です。これは、世帯収入、教育レベルなど、さまざまなフィーチャが地図上でどの程度密接にグループ化されているかを測定するために、地理や地理情報科学 (GIS)でよく使用されます。
モランの I: 公式
Moran の I を計算する式は次のとおりです。
I = (N/W)*ΣΣw ij (x i – x )(x j – x )/Σ(x i – x ) 2
金:
- N: iとjによってインデックス付けされた空間単位の数
- W:すべての w ijの合計
- x:関心のある変数 (世帯収入、就学年数など)
- x : x の平均
- w ij :空間重みの行列
ほとんどの統計ソフトウェアで計算できるため、この測定値を手動で計算する必要はおそらくありませんが、内部で使用される式を知っておくと役立ちます。
Moran の I の値の範囲は -1 から 1 までです。
- -1:対象の変数は完全に分散しています
- 0:対象の変数はランダムに分散されます
- 1:対象の変数は完全にグループ化されています
ほとんどの統計ソフトウェアは、Moran’s I の計算に加えて、データがランダムに分散しているかどうかを判断するために使用できる対応する p 値を計算します。
Moran 検定では、次の帰無仮説と対立仮説を使用します。
帰無仮説 (H 0 ):データはランダムに分散しています。
対立仮説 ( HA ):データはランダムに分散されていません。つまり、データは目に見えるパターンでグループ化されています。
Moran の I に対応する p 値が特定の有意レベル (つまり、α = 0.05) を下回る場合、帰無仮説を棄却し、データが空間的にクラスター化される可能性が低いほど空間的にクラスター化されていると結論付けることができます。偶然に起こった。
モランの I: いくつかの例
次の例は、モランの I の異なる値を持つ偽のカードを表しています。
地図上の各四角形が郡を表し、平均世帯収入が 50,000 ドルを超える郡が青色で示されていると仮定します。
Moran の I = 0:平均世帯収入はランダムに分散しています (つまり、ランダムな領域にランダムなクラスターが存在します)。
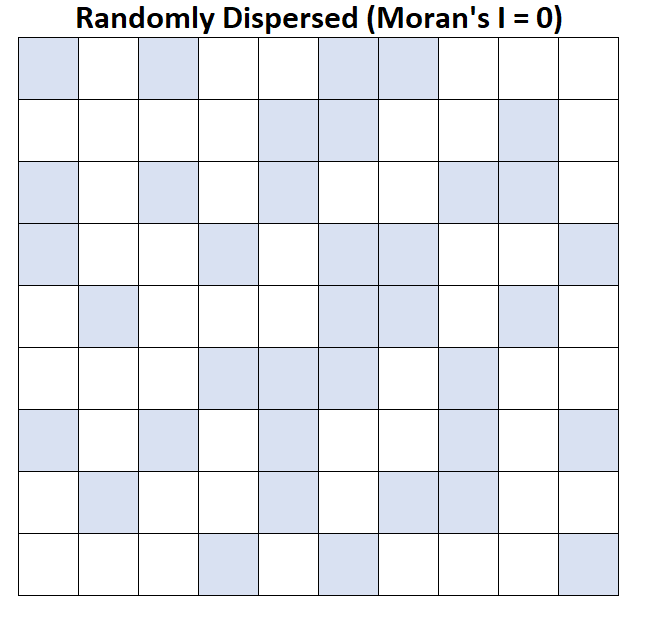
Moran の I = -1:平均世帯収入は完全に分散しています。
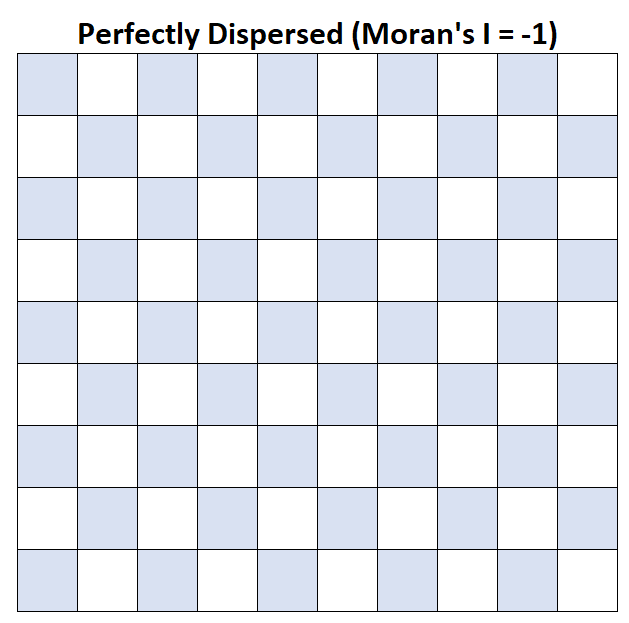
Moran の I = 1:平均世帯収入は完全にグループ化されています。
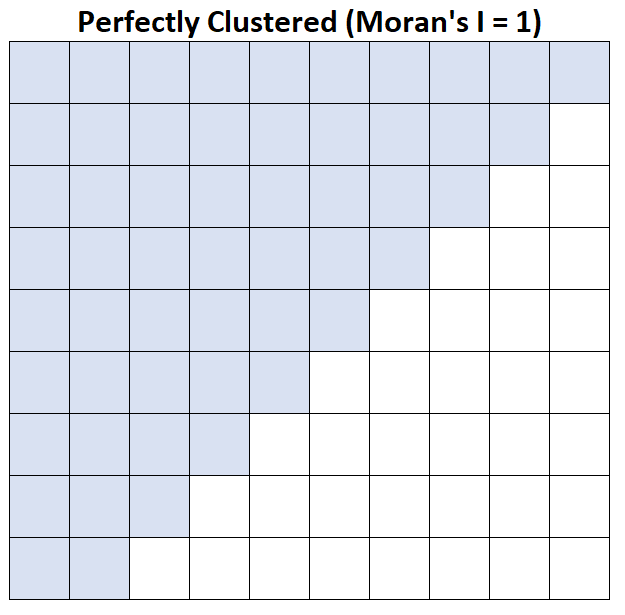
統計ソフトRでのMoran’s Iの具体的な計算例はこちらの例を参照してください。