統計において最頻値が重要なのはなぜですか?
モードは、データ セット内で最も頻繁に現れる値を表します。
データ セットには、モードがない (値が繰り返されない場合)、1 つのモード、または複数のモードを持つことができます。
たとえば、次のデータセットのモードは 19 です。
データセット: 3、4、11、15、19、19、19、22、22、23、23、26
これは最も頻繁に表示される値です。
統計では、次の理由からモードが重要です。
理由 1 : これにより、データ セット内のどの値が最も一般的かを知ることができます。
理由 2 : 平均値と中央値が計算できない場合に、カテゴリ データの最頻値を見つけるのに役立ちます。
理由 3 : 中央値と平均値の方が一般的に使用されますが (この記事で後ほど説明します)、データセットの「中心」がどこにあるのかを知ることができます。
次の例は、実際のこれらの理由をそれぞれ示しています。
理由 1: モードにより、どの値が最も一般的であるかがわかります
米国の住宅の販売価格を含む 100,000 行のデータセットがあるとします。

統計ソフトウェア ( Excel 、 R 、 Pythonなど) を使用してこのデータセットのモードを計算し、次の 3 つのモードがあることが判明したとします。
- 280,000ドル
- 30万ドル
- 305,000ドル
これにより、データセット内の最も一般的な住宅価格がすぐにわかります。
また、モード千の計算は、データの行を調べてどの住宅価格が最も頻繁に発生するかを特定するよりもはるかに高速です。
理由 2: このモードはカテゴリ データで最も一般的な値を検索します。
特定の地域の個人が所有する車の色を示す 1,000 行のデータセットがあるとします。
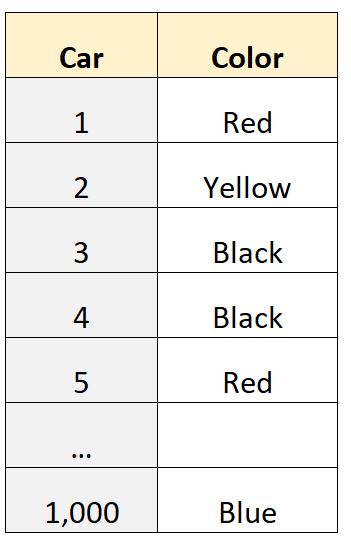
変数「color」はカテゴリ変数です。つまり、値がカテゴリ (「赤」、「黄」、「黒」など) に属しているため、平均や中央値のような定量的な値を計算することはできません。 。
ただし、モードはデータ セット内の最も一般的な値を表すだけであるため、計算することができます。
たとえば、統計ソフトウェアを使用して、このデータセットのモードが「黒」であると判断できます。これにより、このデータセットで最も一般的な車の色が黒であることがわかります。
理由 3: モードにより、データセットの中心がどこにあるのかがわかります。
最頻値は中心傾向の尺度とも考えられます。つまり、データセットの「中心」がどこにあるのかを知ることができます。
たとえば、クラス内の 20 人の異なる生徒の試験の得点を示す次のデータセットがあるとします。

最頻値は82であることが判明しました。これは最も一般的な試験スコアです。これは、このデータセット内の「コア」レビュー スコア値がどこにあるかを示す良い指標であることもわかります。
ただし、代わりに次のような検査結果のデータセットがあるとします。
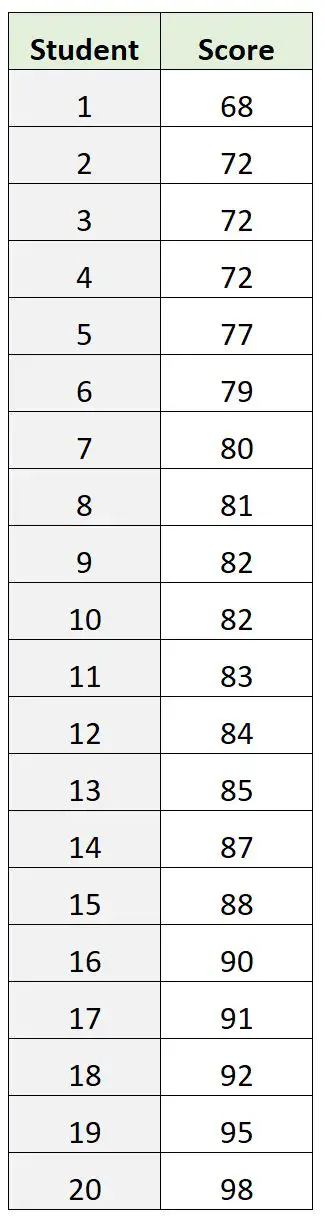
このデータセットでは、 72 がファッション試験のスコアです。ただし、これは試験の「核心」スコアがどこにあるのかを示すのに不十分であることが判明しました。
試験スコアの平均は82.9で、試験スコアの中央値は82.5で、どちらも、ファッションに関して「中心的な」価値がどこにあるのかをよりよく知ることができます。
まとめ
この記事で取り上げる主なポイントを簡単にまとめます。
- モードは、データ セット内で最も頻繁に出現する値を表します。
- このモードは、平均値と中央値が使用できない場合に、カテゴリ データで最も一般的な値を示します。
- このモードにより、データセットの「中心」がどこにあるのかがわかりますが、平均値や中央値と比較すると誤解を招く可能性があります。
追加リソース
次のチュートリアルでは、統計における平均、中央値、最頻値に関する追加情報を提供します。
統計において平均が重要なのはなぜですか?
統計において中央値が重要なのはなぜですか?
具体例: 平均値、中央値、最頻値の使用
平均値と平均値を使用する場合中央値: 例付き