ラテン超立方体サンプリングとは何ですか?

ラテン超立方体サンプリングは、サンプルがサンプル空間全体に均一に分布する乱数をサンプリングするために使用できる方法です。

これは、制御ランダム サンプルと呼ばれるサンプルを生成するために広く使用されており、正確な結果を得るために必要なシミュレーションの数を大幅に削減できるため、モンテカルロ分析によく適用されます。

サンプル紹介

ラテン語ハイパーキューブ サンプリングの概念を理解するために、次の簡単な例を考えてみましょう。

平均が 0、標準偏差が 1 の正規分布データセットから 2 つの値のサンプルを取得したいとします。

このサンプルを取得するために真の乱数発生器を使用した場合、両方の値が 0 より大きいか、両方の値が 0 未満である可能性があります。

ただし、このサンプルを取得するためにラテン超立方体サンプリングを使用した場合、サンプル空間を0 より大きい値を持つ領域に具体的に分割できるため、1 つの値が 0 より大きく、もう 1 つの値が 0 より小さいことが保証されます。値が 0 未満の領域を選択し、各領域からランダムなサンプルを選択します。

1 次元ラテン超立方体サンプリング

1 次元ラテン超立方体サンプリングの背後にある考え方は単純です。指定されたCDF をn 個の異なる領域に分割し、各領域の値をランダムに選択して、サイズnのサンプルを取得します。

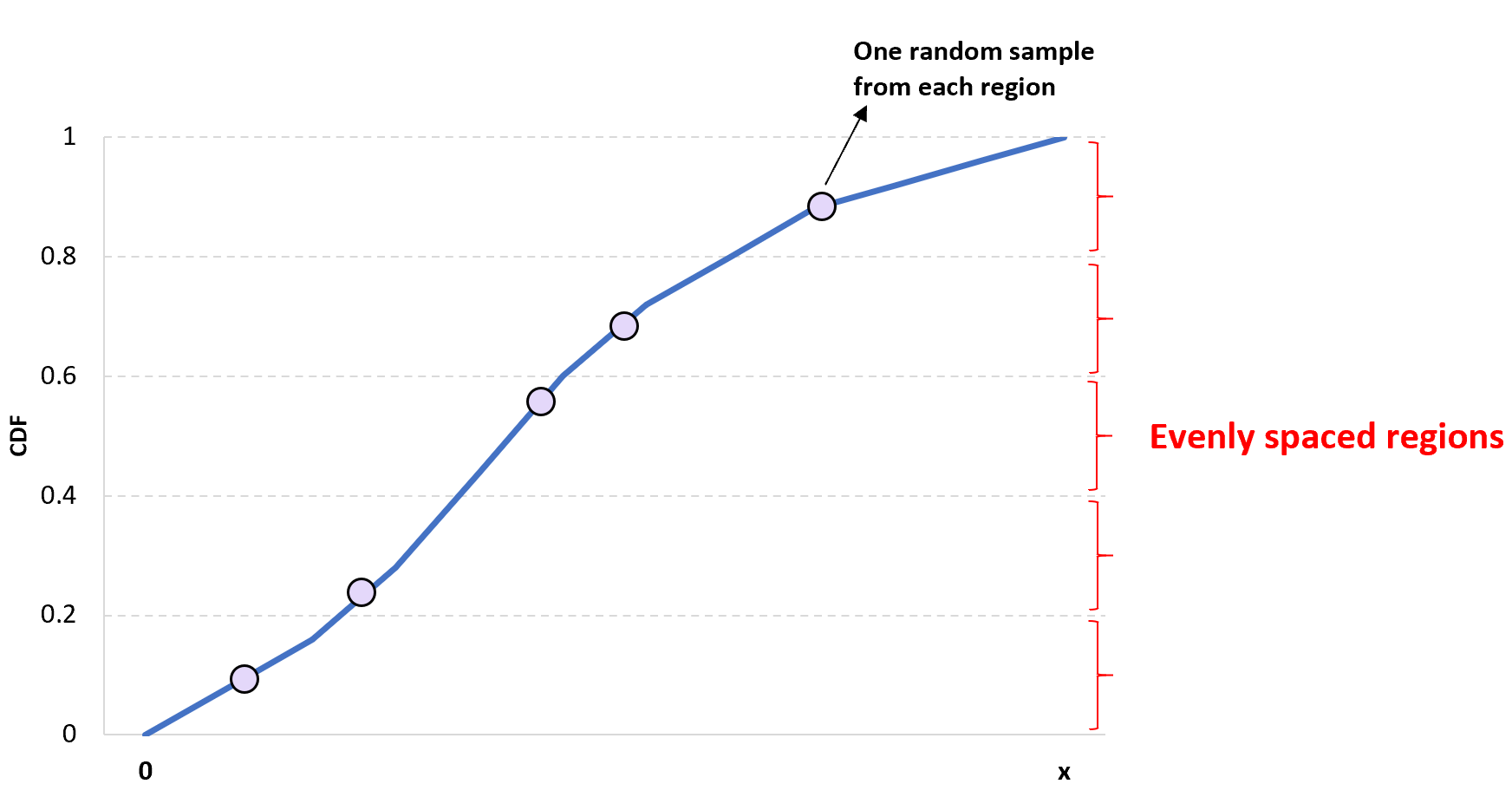
このアプローチの利点は、各領域の少なくとも 1 つの値がサンプルに確実に含まれることです。

2 次元ラテン超立方体のサンプリング

1 次元のラテン超立方体サンプリングのアイデアを 2 次元にも簡単に拡張できます。

2 つの変数 x と y について、各変数のサンプル空間をn 個の等間隔の領域に分割し、各サンプル空間からランダムなサンプルを選択して、2 次元のランダムな値を取得できます。

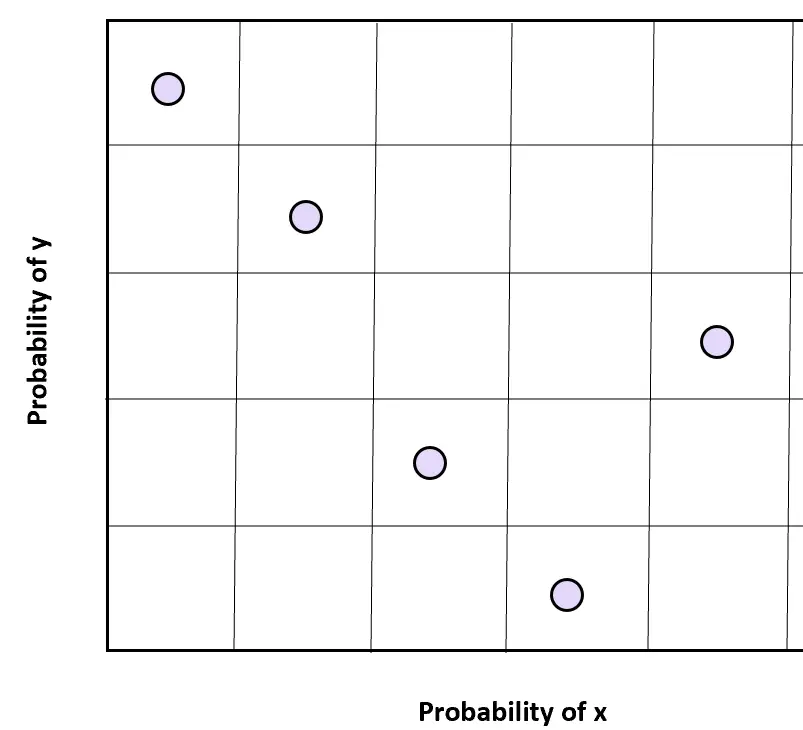
このサンプリング手法で望ましい結果を得るには、2 つの変数が独立している必要があることに注意することが重要です。

N次元ラテン超立方体サンプリング

より大きな次元でラテン超立方体サンプリングを実行するには、2 次元のラテン超立方体サンプリングのアイデアをさらに多くの次元に拡張するだけです。

各変数は単純に等間隔の領域に分割され、各領域からランダム サンプルが選択されて、制御されたランダム サンプルが得られます。

関連:高次元データとは何ですか?

ラテンハイパーキューブサンプリングを使用する理由は何ですか?

ラテン超立方体サンプリングの主な利点は、実際の基礎となる分布を反映するサンプルが生成され、 単純なランダム サンプリングよりもはるかに小さなサンプル サイズが必要になる傾向があることです。

このサンプリング方法は、次元の数が多いデータを扱っており、データの真の基礎となる分布を確実に反映するランダム サンプルを取得する必要がある場合に特に有益です。