レイリー分布の概要
レイリー分布は、ゼロ以上の値のみを取ることができる確率変数をモデル化するために使用される連続確率分布です。
次の確率密度関数があります。
f(x; σ) = (x/σ 2 )e -x 2 /(2σ 2 )
ここで、σ は分布のスケール パラメーターです。
レイリー分布の性質
レイリー分布には次の特性があります。
- 平均: σ√ π/2
- 偏差: ((4-π)/2)σ 2
- モード: σ
π には既知の数値があるため、次のように特性を単純化できます。
- 平均: 1.253σ
- 偏差: 0.429σ2
- モード: σ
レイリー分布の可視化
次のグラフは、スケール パラメーターにさまざまな値を取るときのレイリー分布の形状を示しています。
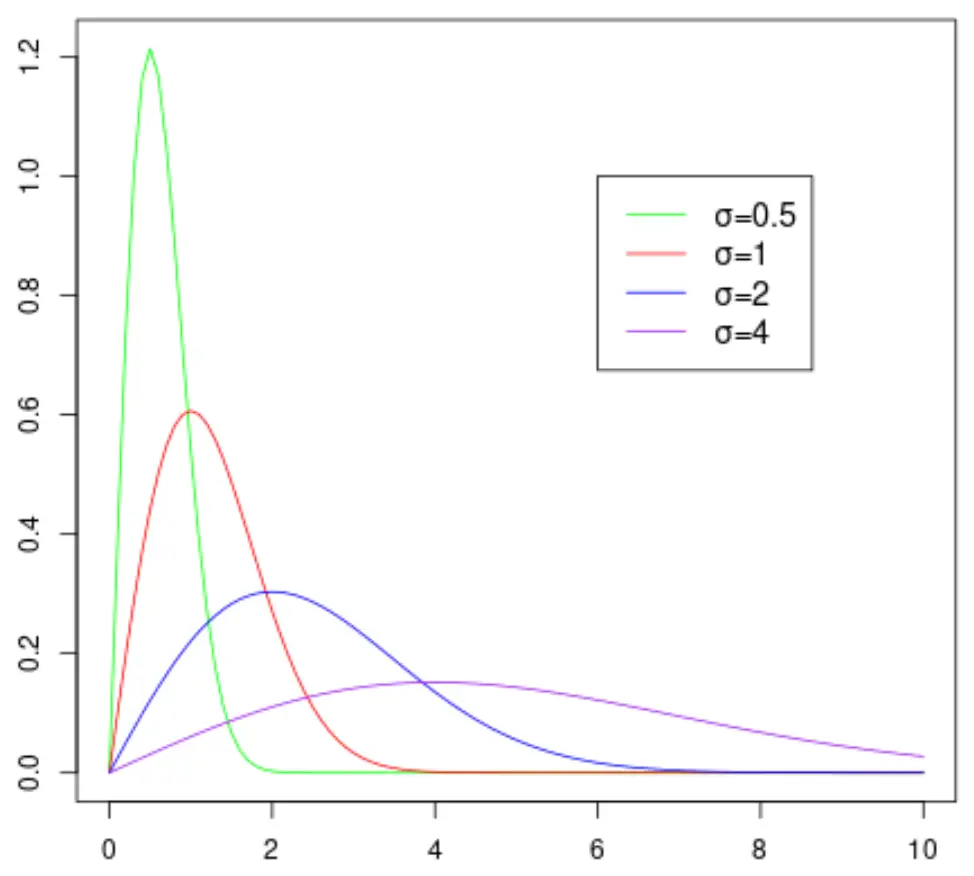
スケールパラメータ σ の値が大きいほど、分布が広くなることに注意してください。
ボーナス:興味がある方のために、次の R コードを使用して上のグラフを生成しました。
#load VGAM package library (VGAM) #create density plots curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green') curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE) curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE) curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE) #add legend legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"), col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)
他のディストリビューションとの関係
レイリー分布には、他の確率分布と次の関係があります。
1.スケール パラメーター (σ)が 1 に等しい場合、レイリー分布は 2 自由度のカイ二乗分布に等しくなります。
2.レイリー分布は、形状パラメータ k = 2 を持つワイブル分布の特殊なケースです。
3.スケール パラメーター σ をもつレイリー分布は、Rice(0, σ) をもつライス分布と等しくなります。
アプリケーション
実際には、レイリー分布は次のようなさまざまなアプリケーションで使用されます。
1.レイリー分布は、波が波頭まで到達するまでの時間や波が到達する最大高さなど、海洋の波の挙動をモデル化するために使用されます。
2.レイリー分布は、MRI としてよく知られる磁気共鳴画像法におけるバックグラウンド データの動作をモデル化するために使用されます。
3.レイリー分布は、人間と動物の栄養レベルと栄養反応の関係をモデル化するために栄養学の分野で使用されます。
追加リソース
次のチュートリアルでは、統計における他の分布に関する追加情報を提供します。