Stata で roc 曲線を作成および解釈する方法
ロジスティック回帰は、応答変数がバイナリの場合に回帰モデルを近似するために使用する統計手法です。ロジスティック回帰モデルがデータセットにどの程度適合しているかを評価するには、次の 2 つの指標を確認します。
- 感度:結果が実際に肯定的な場合に、モデルが観測値に対して肯定的な結果を予測する確率。
- 特異性:結果が実際には陰性である場合に、モデルが観測値に対して陰性の結果を予測する確率。
これら 2 つの指標を視覚化する簡単な方法は、ロジスティック回帰モデルの感度と特異度を表示するグラフであるROC 曲線 を作成することです。
このチュートリアルでは、Stata で ROC 曲線を作成および解釈する方法を説明します。
例: Stata の ROC 曲線
この例では、 lbwというデータセットを使用します。これには、189 人の母親に対する次の変数が含まれています。
- low – 赤ちゃんの出生体重が低いかどうか。 1 = はい、0 = いいえ。
- 年齢– 母親の年齢。
- 喫煙– 母親が妊娠中に喫煙したかどうか。 1 = はい、0 = いいえ。
説明変数として年齢と喫煙を、応答変数として低出生体重を使用して、ロジスティック回帰モデルをデータに当てはめます。次に、ROC 曲線を作成して、モデルがデータにどの程度適合しているかを分析します。
ステップ 1: データをロードして表示します。
次のコマンドを使用してデータをロードします。
https://www.stata-press.com/data/r13/lbw を使用してください
次のコマンドを使用して、データセットを簡単に理解します。
要約する
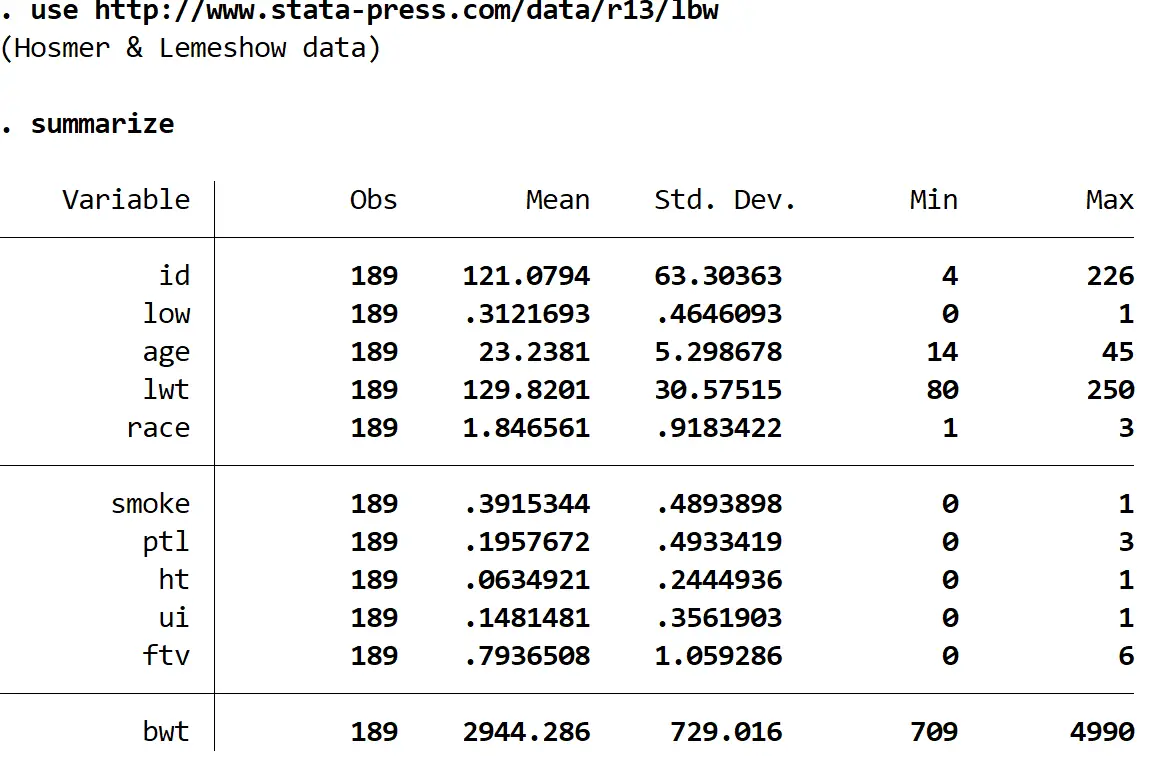
データセットには 11 の異なる変数がありますが、関心があるのは低レベル、年齢、喫煙の 3 つだけです。
ステップ 2: ロジスティック回帰モデルを当てはめます。
次のコマンドを使用して、ロジスティック回帰モデルを当てはめます。
低年齢煙ロジット
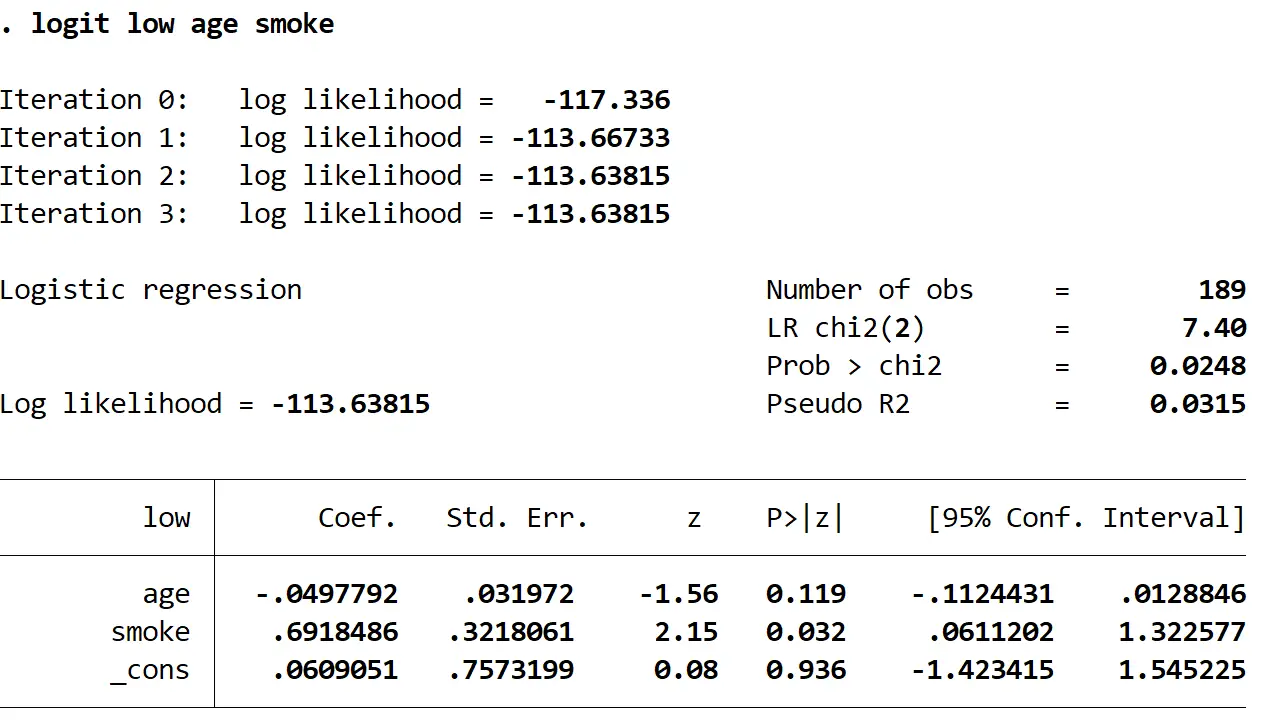
ステップ 3: ROC 曲線を作成します。
次のコマンドを使用して、モデルの ROC 曲線を作成できます。
ロック
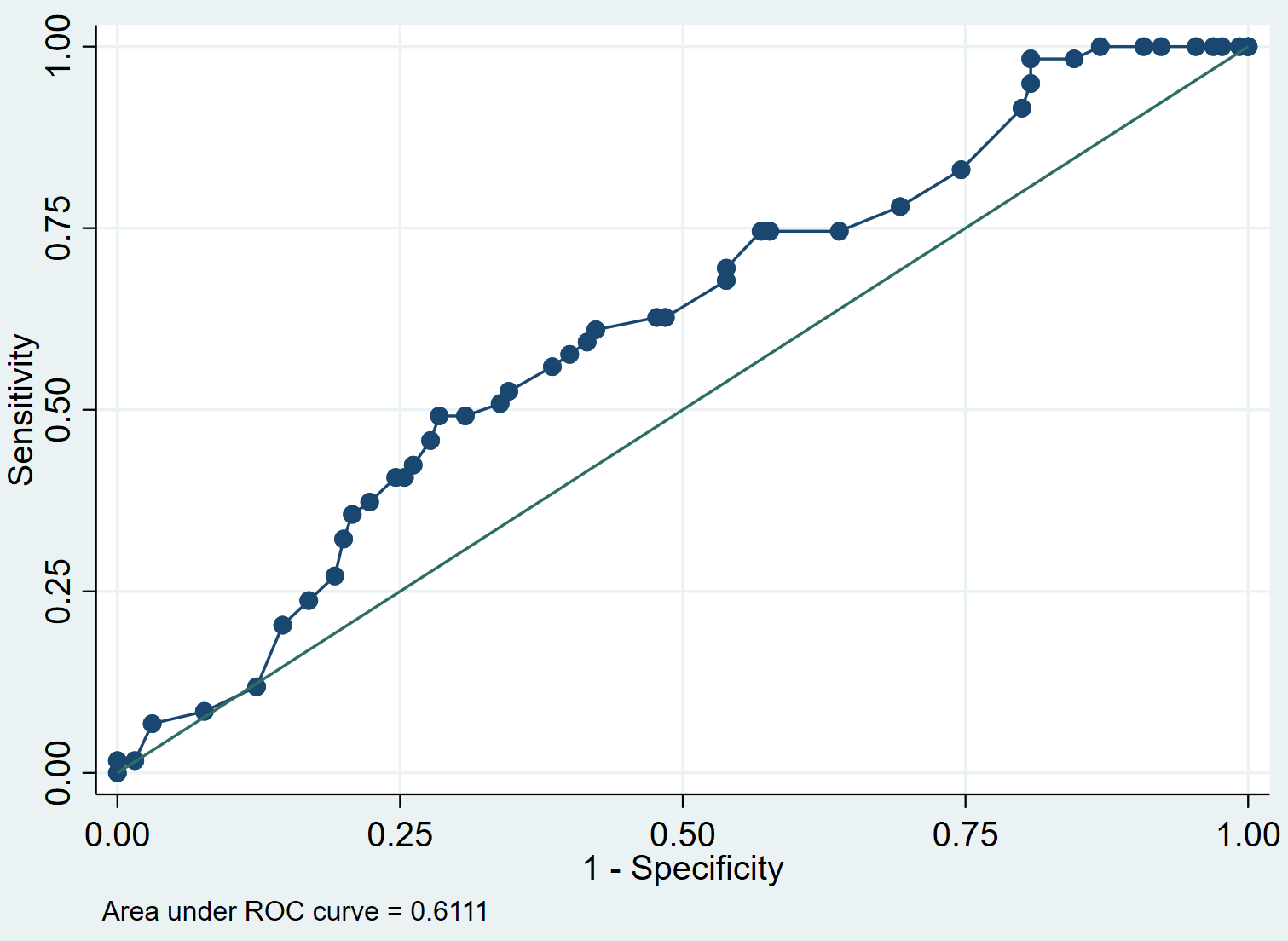
ステップ 4: ROC 曲線を解釈します。
ロジスティック回帰モデルを当てはめると、予測変数の値に基づいて、特定の観測値が肯定的な結果をもたらす確率を計算するために使用できます。
観測値を陽性として分類するかどうかを決定するには、調整された確率がしきい値を超える観測値が陽性として分類され、調整された確率がしきい値を下回るすべての観測値が陰性として分類されるように、しきい値を選択できます。 。
たとえば、しきい値として 0.5 を選択するとします。これは、調整された確率が 0.5 より大きい観測値は陽性の結果を持ち、調整された確率が 0.5 以下の観測値は陰性の結果をもたらすことを意味します。
ROC 曲線は、しきい値が 0 から 1 に変化するときの感度値と特異度 1 を示します。感度と特異度が高いモデルは、プロットの左上隅に沿った ROC 曲線を持ちます。感度と特異性が低いモデルは、対角 45 度に近い曲線になります。
AUC (曲線下面積)は、肯定的な結果と否定的な結果を区別するモデルの能力のアイデアを与えてくれます。 AUC の範囲は 0 から 1 です。AUC が高いほど、モデルは結果を正しく分類できます。この例では、AUC が0.6111であることがわかります。
AUC を使用して、2 つ以上のモデルのパフォーマンスを比較できます。 AUC が最も高いモデルのパフォーマンスが最高になります。