ローレンツ曲線
この記事では、ローレンツ曲線とは何か、またその用途について説明します。母集団のローレンツ曲線を作成する方法を学び、さらに、演習が段階的に解決されるのを確認することができます。最後に、ローレンツ曲線の性質とジニ指数との関係を示します。
ローレンツ曲線とは何ですか?
ローレンツ曲線は、地域の人口の経済的不平等をグラフで表したものです。言い換えれば、ローレンツ曲線は、領土全体にわたる収入の分配の不平等を分析できるようにする曲線です。
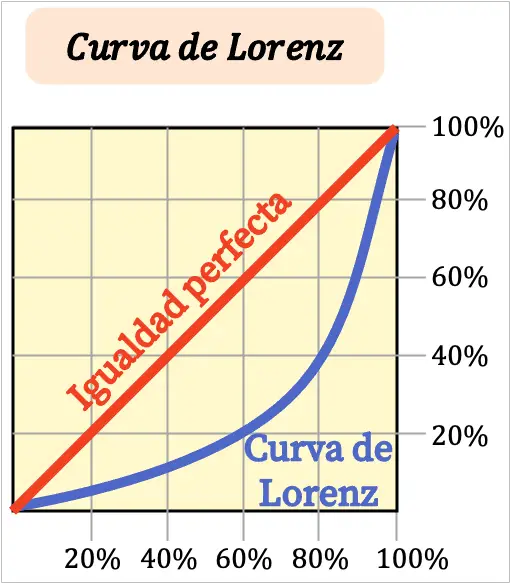
ローレンツ曲線が直線的であればあるほど、領土の収入はより平等になります。一方で、ローレンツ曲線の曲がりが大きいほど、所得の分配はより不平等になります。
通常、ローレンツ曲線の軸はパーセンテージで表されます。グラフの X 軸は人口の割合を表し、一方、Y 軸は所得の割合を示します。
ローレンツ曲線は、20 世紀の非常に重要なアメリカの経済学者であるマックス オットー ローレンツによって 1905 年に発明されました。
ローレンツ曲線の計算方法
ローレンツ曲線の定義を理解したら、この統計曲線がどのように計算されるかを見てみましょう。ローレンツ曲線を定義する公式は存在しますが、実際には一般的には使用されないことに注意してください。そのため、例を段階的に解決して、それがどのように行われるかを確認できるようにします。
- 次の表に所得が示されている人口のローレンツ曲線を表します。
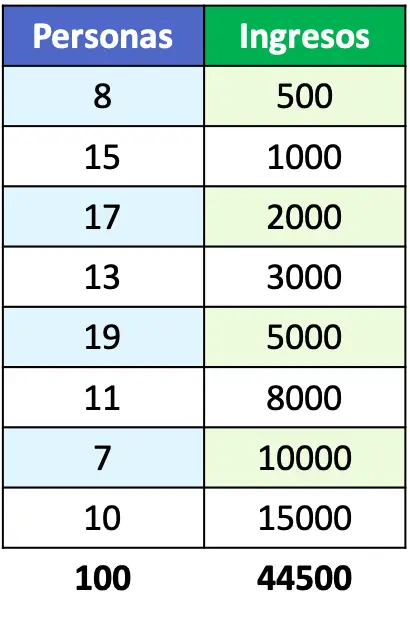
問題文でローレンツ曲線関数の例が示されている場合は、その関数をグラフ上で直接表すことができます。ただし、この場合は人口の収入しか得られないため、各グループの人々の割合を計算する必要があります。
したがって、人口と収入のパーセンテージを決定するには、人口変数のテーブルに 2 つの列を追加する必要があります。
- 累積された絶対頻度 ( Fi ) を含む列。
- 2 番目の列は累積パーセンテージに対応し、累積絶対頻度を総人数で割ることによって計算されます。
一方、収入変数には 3 つの列を追加する必要があります。
- 総収入が計算される列。人数と各人が受け取る収入の積に相当します。
- 総収入の累積絶対頻度 ( Fi ) による 2 番目。
- 3 番目の列には、前の列を人口の合計所得で割ることによって求められる累積パーセンテージが含まれます。
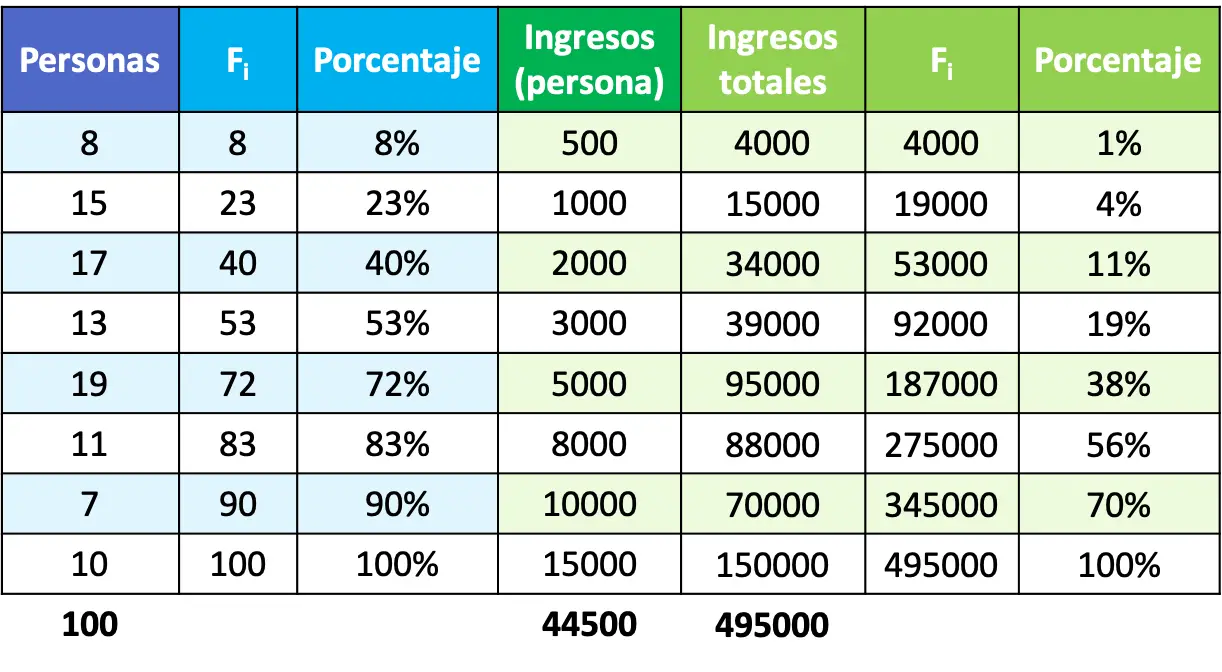
最後に、パーセンテージを計算したので、残っているのはグラフ上に点をプロットし、それらを結合してローレンツ曲線を形成することだけです。 X 軸は人口の割合、Y 軸は収入の割合であることに注意してください。
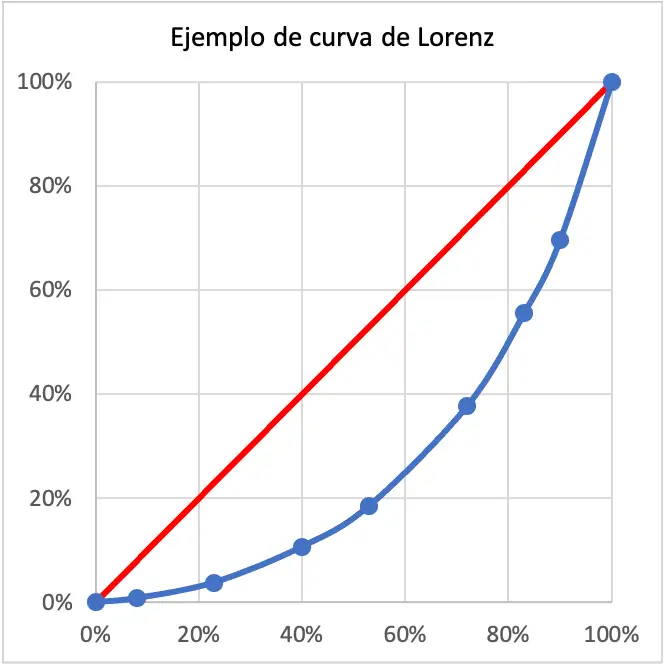
この場合、ローレンツ曲線の幅が非常に広いため、調査対象集団の収入は非常に不平等です。実際、ローレンツ曲線は完全な等価性を表す赤い線から非常に離れています。
ローレンツ曲線の解釈
このセクションでは、母集団のローレンツ曲線を解釈する方法について説明します。これは、グラフの作成方法を知ることに加えて、その意味を理解する必要があるためです。
ローレンツ曲線は、人口の何パーセントが領土の総収入の何パーセントを所有しているかを示します。たとえば、上に示したローレンツ曲線の例では、人口の 40% が全人口所得の 11% に相当する所得を持っています。つまり、非常に不均一な領域なのです。
したがって、ローレンツ曲線は、国または地域の住民間の収入の平等または不平等を視覚的に表します。完全な平等を示す線から遠ざかるほど、国民の所得はさらに不平等になることを意味します。一方、ローレンツ曲線が右に近づくほど、国民の所得がより公平に分配されていることを意味します。
さらに、あるローレンツ曲線がグラフ全体で別のローレンツ曲線より上にある場合、これは、最初の集団の収入が 2 番目の集団の収入よりも等しいことを意味します。
ローレンツ曲線とジニ係数
記事全体で説明したように、ローレンツ曲線は、領土の収入がどのように分配されているか、そして領土がどれほど不平等であるかをグラフで示します。
一方、ジニ係数はジニ指数とも呼ばれ、地域の経済的不平等を数値で示します。
したがって、ローレンツ曲線とジニ係数はリンクされています。実際、国のジニ係数はローレンツ曲線から計算できます。次の記事でこれを行う方法について説明します。
ローレンツ曲線の性質
ローレンツ曲線には次の特性があります。
- ローレンツ曲線は常に点 (0,0) で始まり (100,100) で終わります。
- サンプル平均がゼロの場合、ローレンツ曲線は定義されません。
- ローレンツ曲線は、完全な等価線より上のグラフには現れません。
- 収入がマイナスにならないと仮定すると、ローレンツ曲線は常に増加します。