Stata で一元配置分散分析を実行する方法

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

このタイプの検定は、応答変数に対する予測変数の影響を分析するため、一元配置分散分析と呼ばれます。代わりに、応答変数に対する 2 つの予測変数の影響に興味がある場合は、二元配置ANOVAを実行できます。

このチュートリアルでは、Stata で一元配置分散分析を実行する方法について説明します。

例: Stata での一元配置分散分析

この例では、 systolicという組み込みの Stata データセットを使用して、一元配置分散分析を実行します。このデータセットには、58 人の異なる個人に関する次の 3 つの変数が含まれています。

• 使用した薬剤
• 患者の病気
• 最高血圧の変化

次の手順を使用して一元配置分散分析を実行し、使用される薬剤の種類が収縮期血圧の変化に重大な影響を与えるかどうかを判断します。

ステップ 1: データをロードします。

まず、コマンド ボックスにwebuse systolicと入力し、Enter をクリックしてデータをロードします。

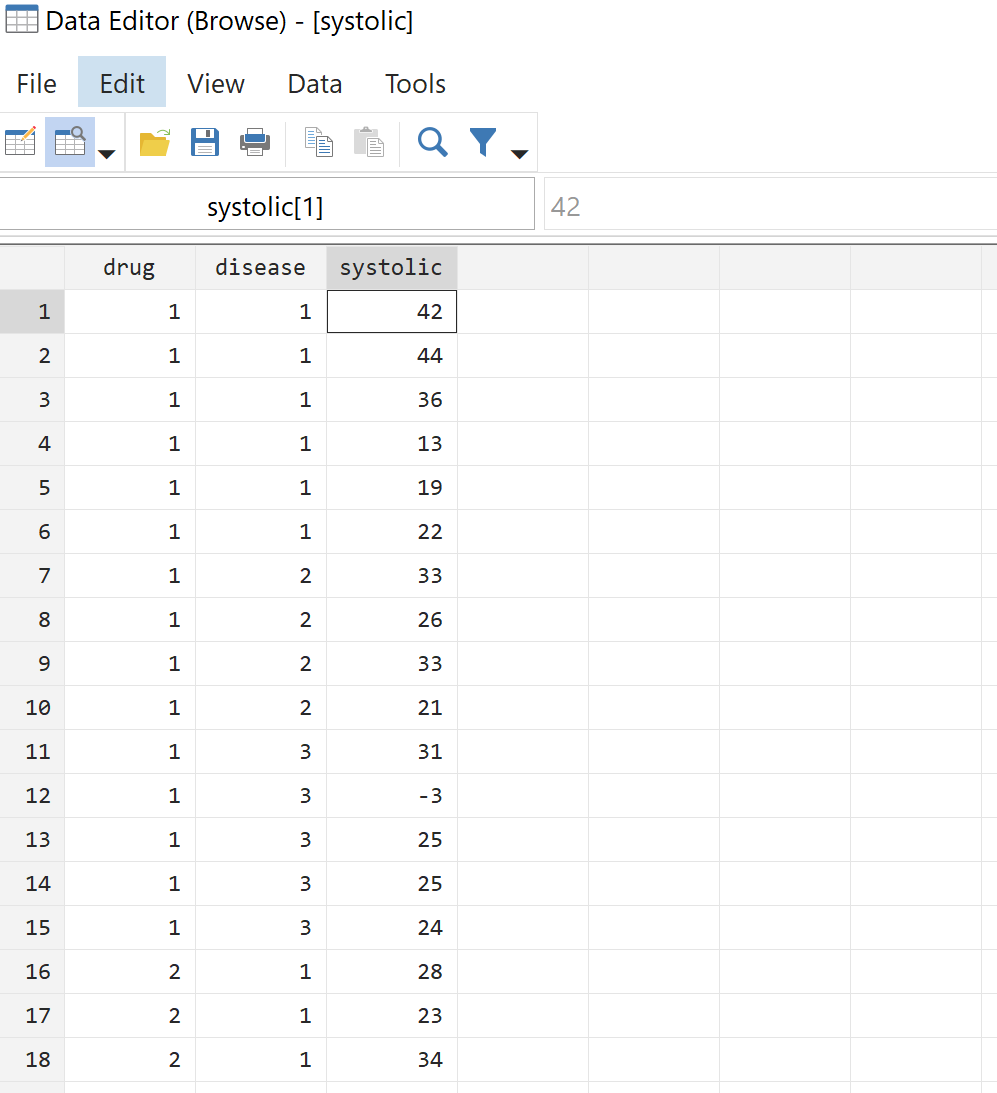
ステップ 2: 生データを表示します。

一元配置分散分析を実行する前に、まず生データを見てみましょう。上部のメニュー バーから、 [データ] > [データ エディター] > [データ エディター (参照)]に移動します。これにより、58 人の患者全員の実際のデータが表示されます。

ステップ 3: データを視覚化します。

次に、データを視覚化してみましょう。 箱ひげ図を作成して、各薬物カテゴリーの最高血圧値の分布を表示します。

上部のメニュー バーから、 [グラフ] > [箱ひげ図]に移動します。変数で、[Systolic] を選択します。

次に、「グループ化変数」の下の「カテゴリー」小見出しで、薬物を選択します。

「OK」をクリックします。 4 つの箱ひげ図を含むグラフが自動的に表示されます。

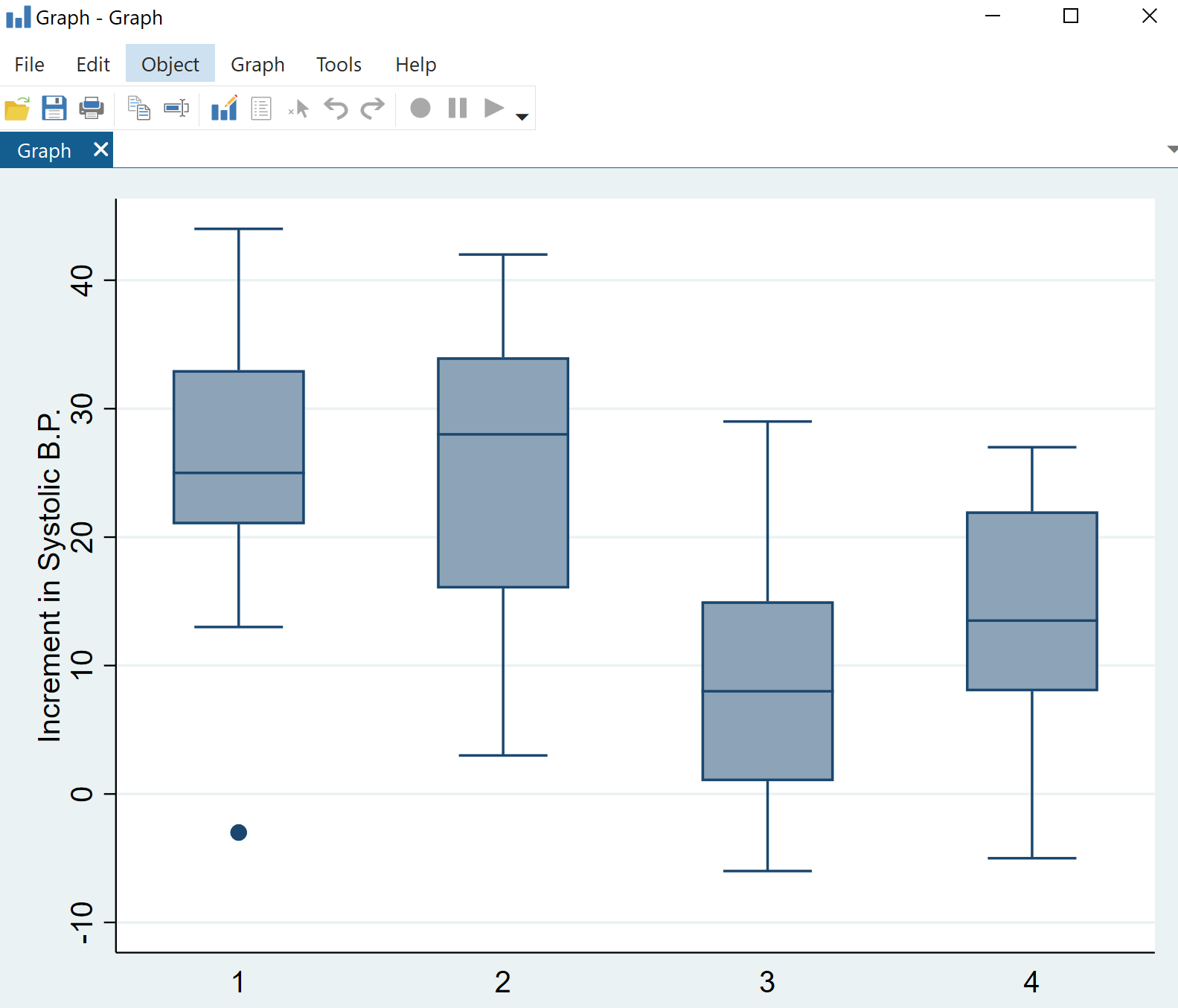
収縮期血圧の変化の分布が薬剤カテゴリーによって異なることはすぐにわかりますが、一元配置分散分析により、これらの違いが統計的に有意であるかどうかがわかります。

ステップ 4: 一元配置分散分析を実行します。

上部のメニュー バーから、 [統計] > [線形モデルおよび関連モデル] > [ANOVA/MANOVA] > [一元配置 ANOVA]に移動します。

[応答変数] で、[シストリック] を選択します。因子変数で薬剤を選択します。次に、 「要約テーブルの作成」の横にあるボックスをクリックすると、各グループの基本的な記述統計が表示されます。次に、 「OK」をクリックします。

次の出力が表示されます。

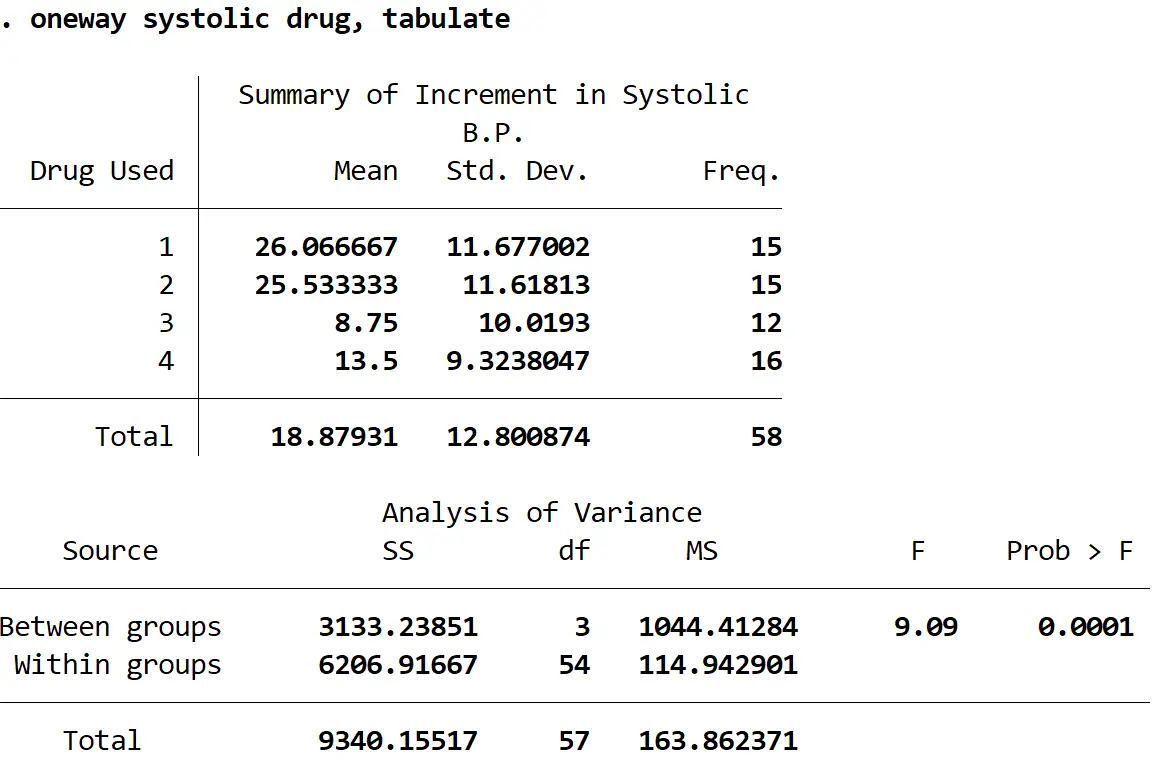
F 統計量は9.09で、対応する p 値は0.0001です。 p 値は alpha = 0.05 より小さいため、各グループの収縮期血圧の平均変化が等しいという帰無仮説を棄却できます。

言い換えれば、少なくとも 2 つの薬物グループ間の収縮期血圧の平均変化には統計的に有意な差があります。

ステップ 5: 複数の比較テストを実行します。

次に、いくつかの比較テストを実行して、どのグループ平均が互いに異なるかを実際に確認できます。

上部のメニュー バーから、 [統計] > [要約、表、検定] > [要約統計量と記述統計量] > [平均のペアごとの比較]に移動します。

[変数] で、収縮期応答変数を選択します。 [Over] には、説明変数Drugを選択します。 [多重比較の調整] では、 Tukey 法を選択します。

次に、 [レポート] の小見出しの下で、 [効果の表]の横にあるボタンをクリックし、 [信頼区間と p 値を含む効果の表を表示]の横のボックスをオンにします。次に、 「OK」をクリックします。

次の結果が表示されます。

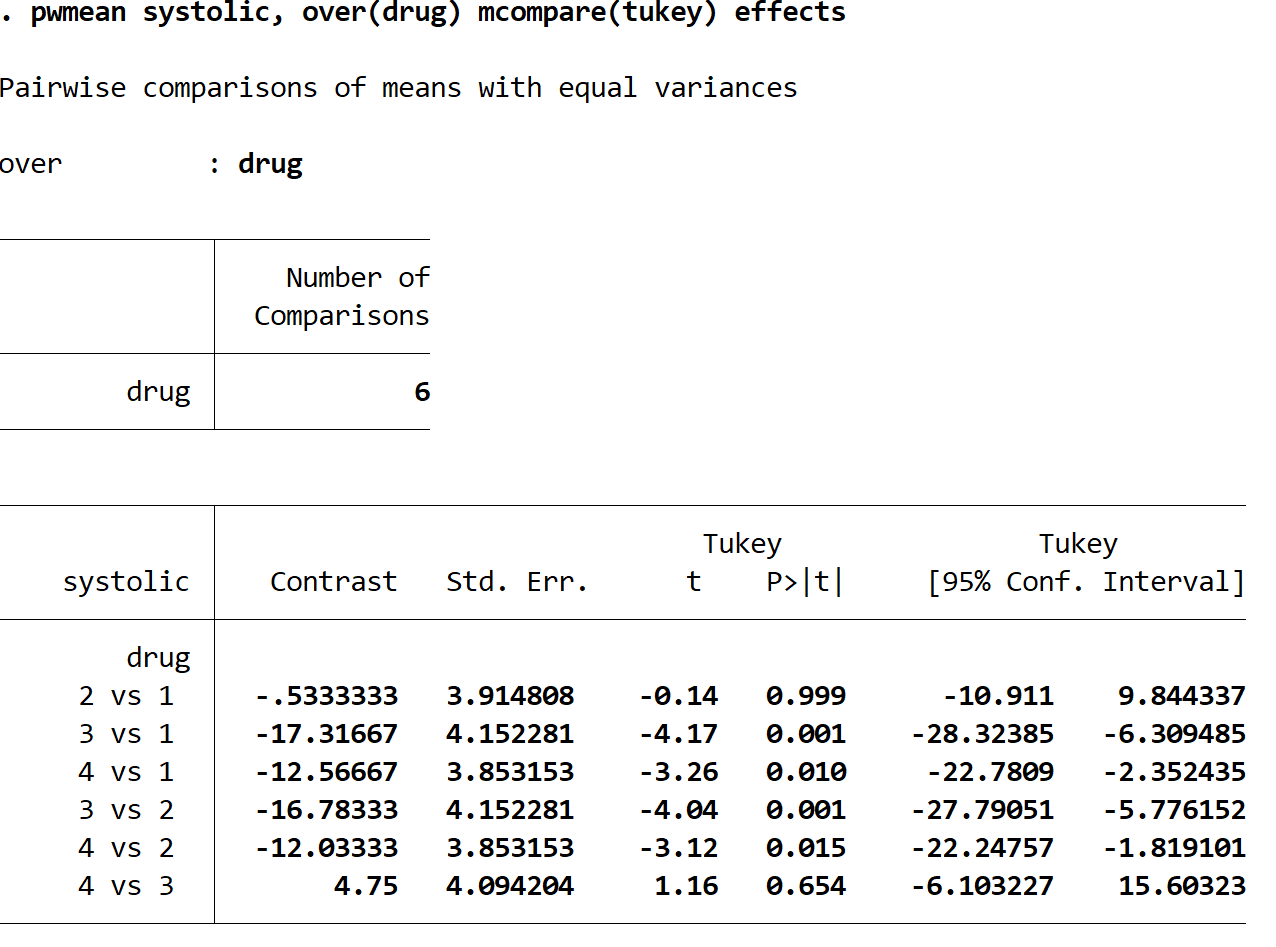
各行は、2 つの特定の薬物グループ間の比較を表します。たとえば、最初の行は、薬物グループ 2 と薬物グループ 1 の間の収縮期血圧の平均変化を比較しています。この比較の p 値は0.999で、これは非常に高く、0.05 以上です。これは、薬物グループ 1 と 2 の間に統計的に有意な差がないことを意味します。

ただし、次の比較の p 値はすべて 0.05 未満であることがわかります。

• 薬 3 対 1 | p値 = 0.001
• 薬 4 対 1 | p値 = 0.010
• 薬 3 対 2 | p値 = 0.001
• 薬 4 対 2 | p値 = 0.015

これは、収縮期血圧の平均変化の差がこれらの各グループ間で統計的に有意であることを意味します。

ステップ 6: 結果を報告します。

最後に、一元配置分散分析の結果を報告します。これを行う方法の例を次に示します。

一元配置分散分析を実行して、4 つの異なる種類の薬剤が収縮期血圧に異なる影響を与えるかどうかを判断しました。

次の表は、各グループの参加者数、各グループの収縮期血圧の平均変化と収縮期血圧の標準偏差をまとめたものです。

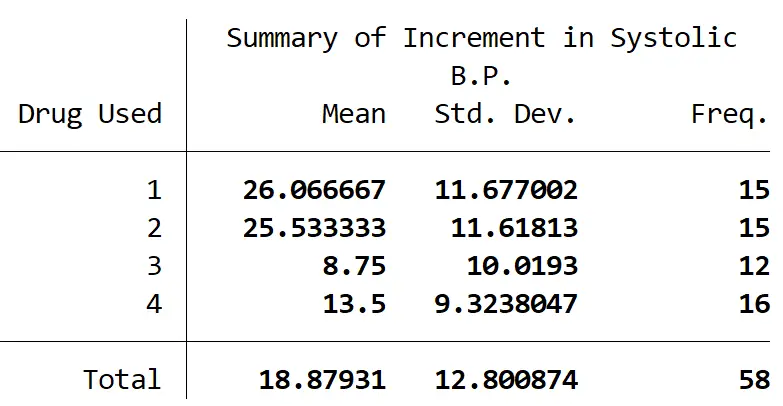
一元配置分散分析により、少なくとも 2 つのグループ間に統計的に有意な差があることが明らかになりました (F(3, 54) = 9.09、p = 0.001)。

多重比較のための Tukey 検定により、収縮期血圧の変化は薬剤 1 より薬剤 3 の方が統計的に有意に高く (17.32 +/- 4.15、p = 0.001)、薬剤 2 と比較して薬剤 3 の方が統計的に有意に高かった (16.78 +/- 4.15、p = 0.001)。 p = 0.001)、薬剤 4 と薬剤 1 の比較 (12.57 +/- 3.85、p = 0.010)、薬剤 4 と薬剤 2 の比較 (12.03 +/- 3.85、p = 0.015)。

薬物グループ 1 と 2 の間 (0.533 +/- 3.91、p = 0.999)、または薬物グループ 3 と 4 の間 (4.75 +/- 4.09、p = 0.654) に統計的に有意な差はありませんでした。