定分散仮説: 定義と例

によるベンジャミン・アンダーソン博士 7月 23, 2023 ガイド 0コメント

線形回帰は、1 つ以上の予測変数と応答変数の間の関係を定量化するために使用される手法です。

線形回帰の重要な仮定の 1 つは、予測変数の各レベルで残差の分散が一定であるということです。

この仮定が検証されない場合、残差は不均一分散性の影響を受けることになります。これが起こると、モデルの係数推定の信頼性が低くなります。

回帰モデルの残差に一定の分散があるかどうかを判断する最も一般的な方法は、残差に対する近似値のプロットを作成することです。

これは、x 軸に沿って回帰モデルの近似値を表示し、y 軸に沿って近似した値の残差を表示するタイプのプロットです。

残差の分布が近似値の各レベルでほぼ等しい場合、一定分散の仮定が満たされていると言えます。

そうしないと、残差の分散が系統的に増加または減少する場合、この仮定が破られる可能性があります。

注: このタイプのプロットは、回帰モデルをデータセットに適合させた後にのみ作成できます。

次のグラフは、一定の分散を表示する近似値と残差のプロットの例を示しています。

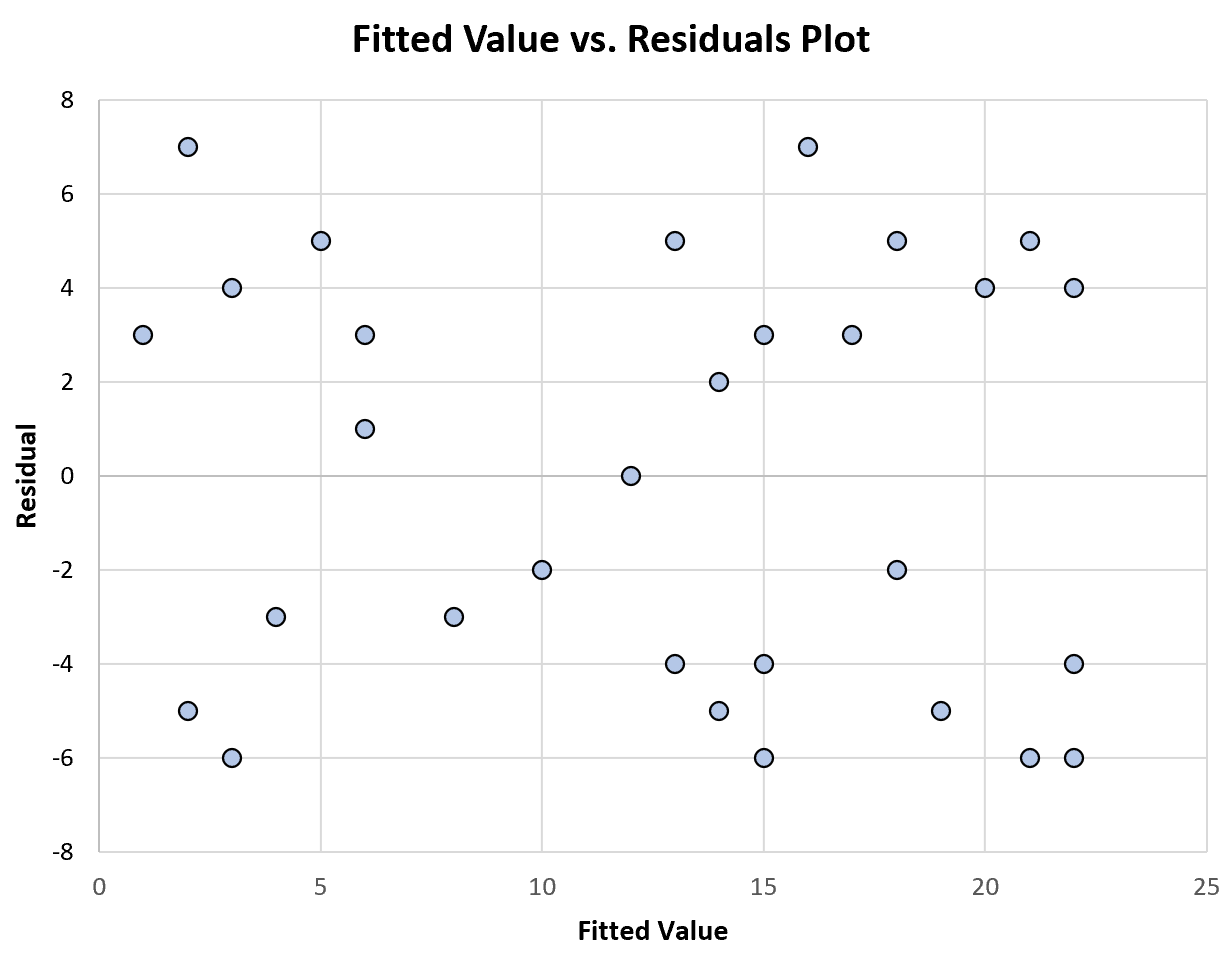
残差が特定のパターンではなくゼロの周囲にランダムに分散しており、近似値の各レベルでほぼ一定の分散を示していることに注目してください。

次のグラフは、非定数分散を表示する近似値と残差のプロットの例を示しています。

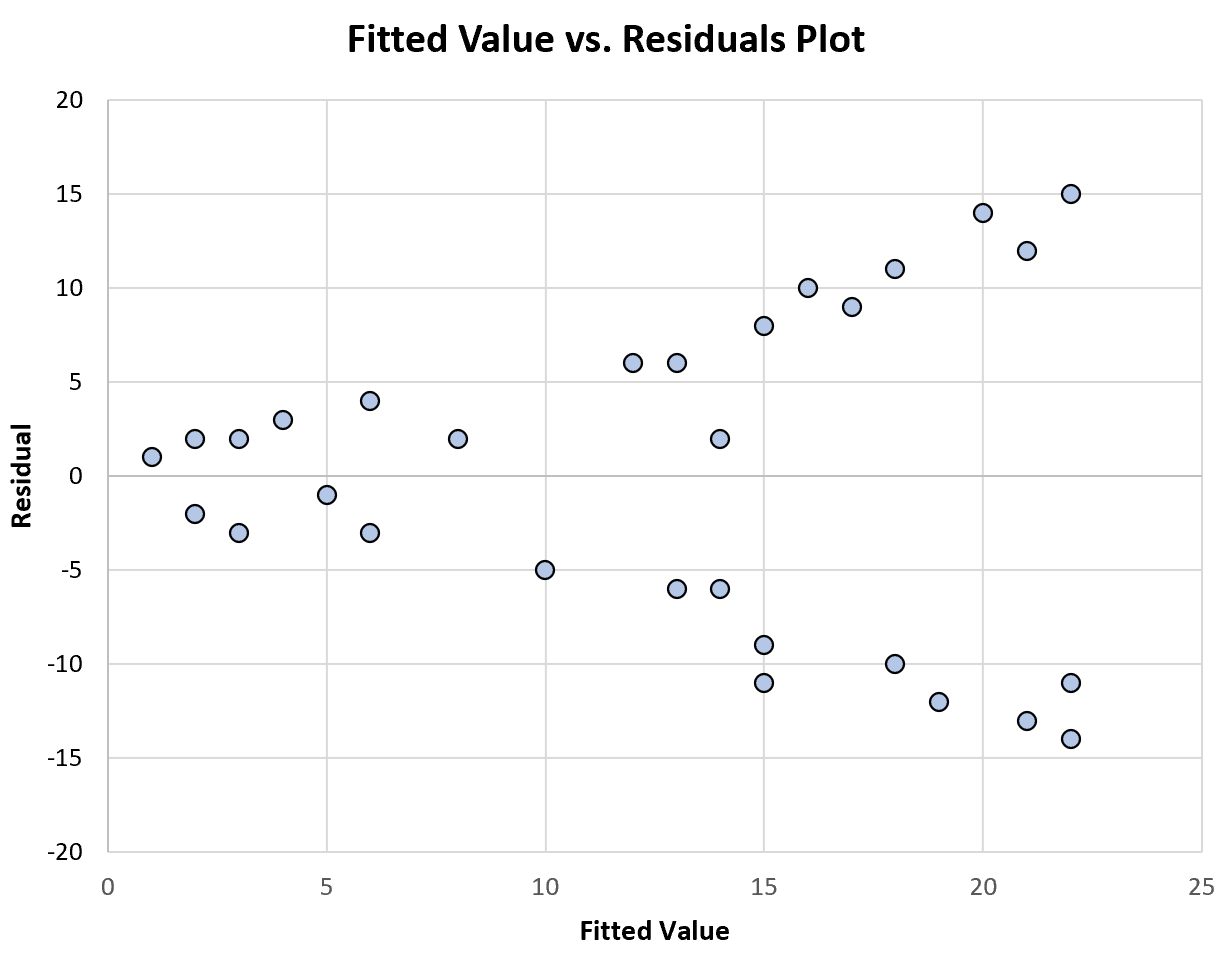
近似値が増加するにつれて、残差の分布が大きくなることに注意してください。これは、非一定の分散の典型的な兆候です。

これは、回帰モデルが残差の非一定分散の影響を受けており、したがってモデルの係数推定が信頼できないことを示しています。

一定の分散の仮定に違反した場合、この問題を解決する最も一般的な方法は、次の 3 つの変換のいずれかを使用して応答変数を変換することです。

1. 対数変換:応答変数を y からlog(y)に変換します。

2. 平方根変換:応答変数を y から√yに変換します。

3. 立方根変換:応答変数を y からy ^1/3に変換します。

これらの変換を実行すると、非定数分散の問題は通常解消されます。

次のチュートリアルでは、線形回帰と残差分析に関する追加情報を提供します。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る