三元配置分散分析: 定義と例

三元配置分散分析は、 3 つの異なる要因が応答変数にどのような影響を与えるかを決定するために使用されます。

三元配置分散分析は、一元配置分散分析(因子が 1 つだけ) や二元配置分散分析(因子が 2 つだけ) よりも一般的ではありませんが、依然としてさまざまな分野で使用されています。

三元分散分析を実行するときは常に、各因子と応答変数の間に統計的に有意な関係があるかどうか、また因子間に相互作用効果があるかどうかを知りたいと考えます。

このチュートリアルでは、3 元配置分散分析を使用できるいくつかのシナリオと、その実行方法の例を示します。

三元配置分散分析を使用する場合

3 元配置 ANOVA を使用できるいくつかのシナリオを次に示します。

シナリオ 1: 植物学

植物学者は、(1) 日光への曝露、(2) 水やりの頻度、および (3) 肥料の種類が植物の成長にどのような影響を与えるかを判断したい場合があります。

このシナリオでは、3 つの因子と 1 つの応答変数があるため、3 元分散分析を実行できます。

シナリオ 2: 小売業

小売店のマネージャーは、(1) 曜日、(2) 店舗の場所、(3) 広告キャンペーンが総売上にどのように影響するかを判断したい場合があります。

このシナリオでは、3 つの因子と 1 つの応答変数があるため、3 元分散分析を実行できます。

シナリオ 3: 医療

医師は、(1) 性別、(2) 食事、(3) 運動習慣が体重にどのように影響するかを判断したい場合があります。

このシナリオでは、3 つの因子と 1 つの応答変数があるため、3 元分散分析を実行できます。

三元配置分散分析: 例

研究者が、トレーニング プログラム、性別、スポーツ部門がジャンプの高さに影響を与えるかどうかを判断したいとします。

これをテストするために、次の要素を使用して 3 元配置分散分析を実行できます。

• 1. トレーニング プログラム(プログラム 1 とプログラム 2)
• 2. 性別（男性または女性）
• 3. スポーツ部門（部門 I 対部門 II）

唯一の応答変数はジャンプの高さです。

彼が 40 人に関するこのデータを収集したとします。

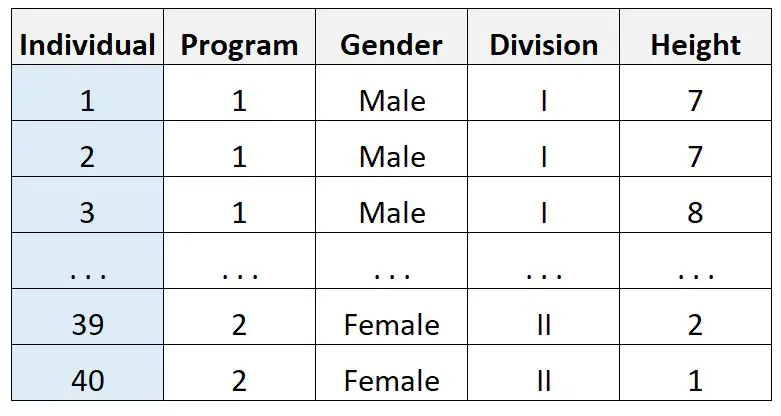
次に、統計ソフトウェアを使用して三元分散分析を実行し、次の結果を受け取ります。

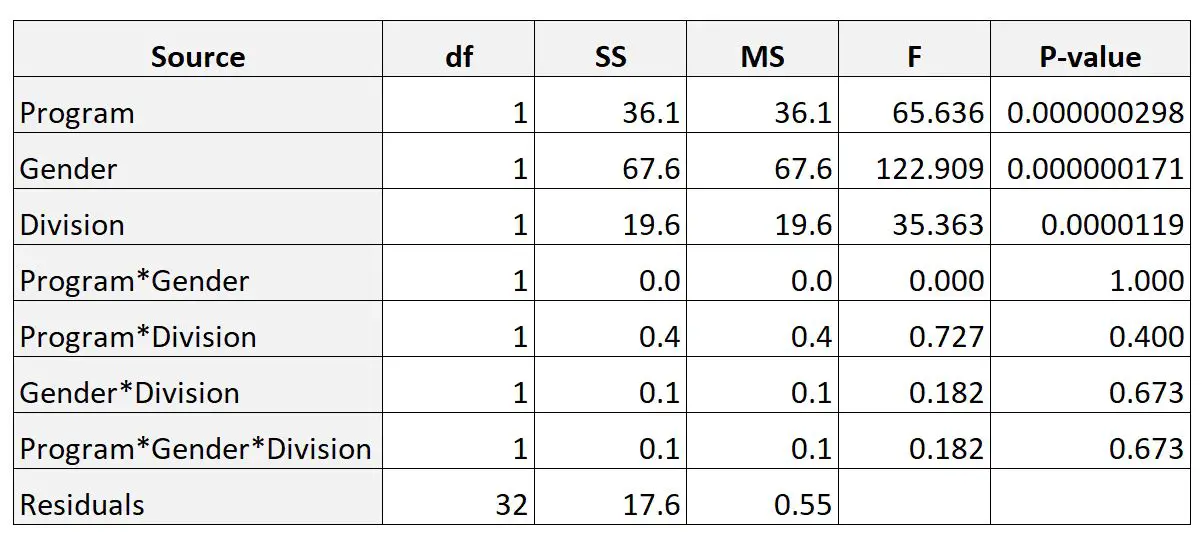
[P 値]列には、個々の因子の P 値と因子間の交互作用が表示されます。

結果から、3 つの因子間の相互作用はどれも統計的に有意ではなかったことがわかります。

また、3 つの要素 (プログラム、性別、部門) のそれぞれが統計的に有意であることもわかります。

結論として、トレーニング プログラム、性別、部門はすべて、選手のジャンプ高さの向上を示す重要な指標であると言えます。

また、これら 3 つの要素の間には有意な相互作用効果はないと言えます。

注: 実際には、各プログラム、性別、部門の平均ジャンプ高も計算して、各要因のどのレベルがジャンプ高の増加に関連しているかを判断できます。

追加リソース

次のチュートリアルでは、R と Python で 3 元配置分散分析を実行する方法について説明します。

R で三元配置分散分析を実行する方法
Python で三元配置分散分析を実行する方法