三角分布の概要
三角分布は、三角形の確率密度関数を持つ連続確率分布です。
これは 3 つの値によって定義されます。
- 最小値は
- 最大値b
- 最大値c
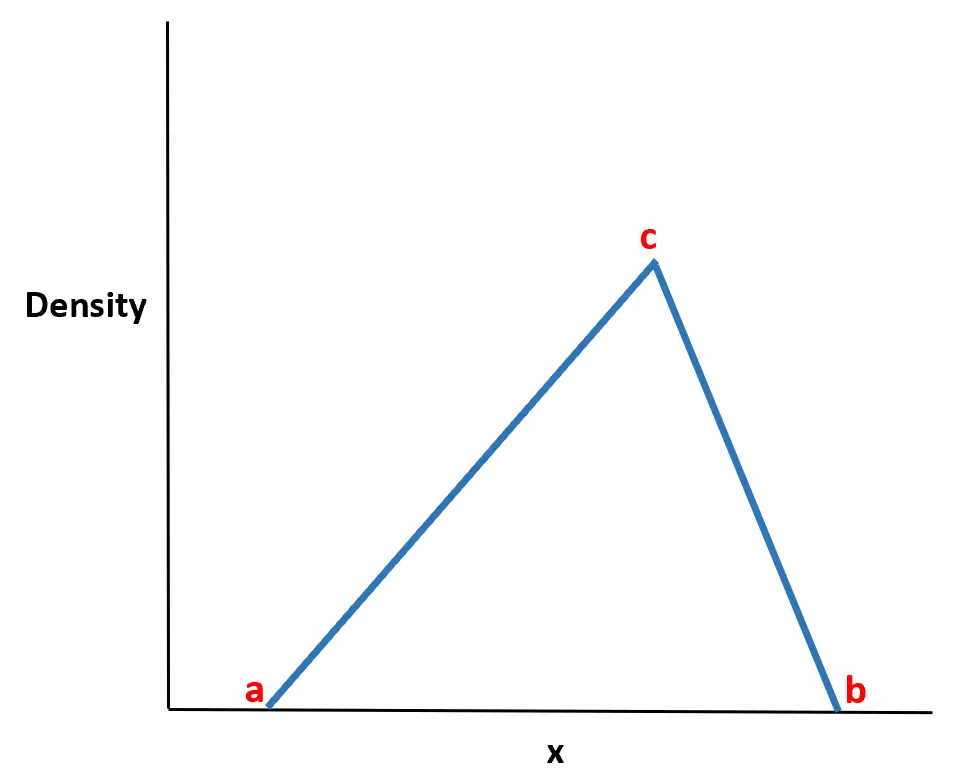
分布の名前は、確率密度関数が三角形の形状をしていることに由来しています。
この分布は、確率変数が取る最小値 (a)、最大値 (b)、および最も可能性の高い値 (c) を推定できることが多いため、現実の世界では非常に役立つことがわかります。多くの場合、これら 3 つの値だけがわかっている三角分布を使用して、確率変数の動作をモデル化できます。
たとえば、レストランは、来週の総売上高が最低 10,000 ドル、最高 30,000 ドル、おそらく 25,000 ドルになると見積もるとします。

これら 3 つの数値だけを使用すると、三角分布を使用して、特定の数の販売が行われる確率を決定できます。
三角分布の性質
三角分布には次の特性があります。
PDF:
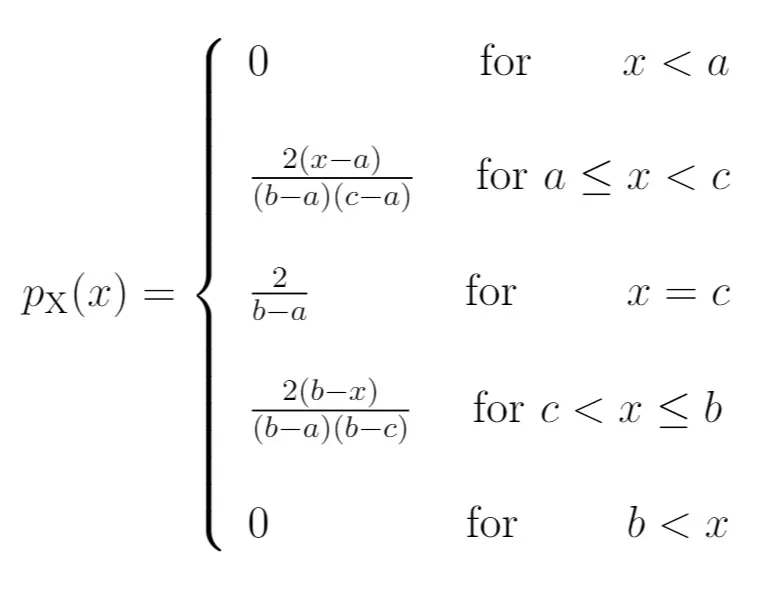
CDF:
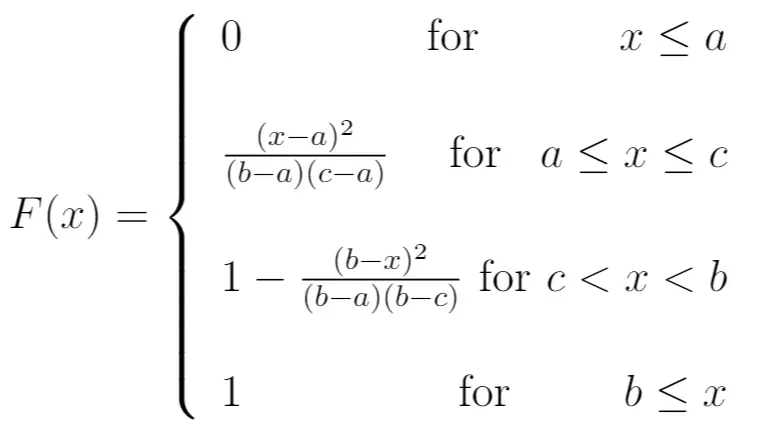
平均: (a + b + c) / 3
モード: c
分散: (a 2 + b 2 + c 2 – ab – ac – bc) / 18
三角分布の使用例
前の例に戻りましょう。レストランが、来週の総売上高が最低 10,000 ドル、最高 30,000 ドル、おそらく 25,000 ドルになると見積もっているとします。

レストランの総売上高が 20,000 ドル未満になる確率はどれくらいですか?
この質問に答えるには、x = 総売上高を求めることができます。 x は最小値aの $10,000 と最大値cの $25,000 の間にあることがわかります。
したがって、PDF によると、次の方程式を使用して、レストランの総売上高が 20,000 ドル未満である確率を求めることができます。
- P(X < $20,000) = (xa) 2 / ((ba)(ca))
- P(X < $20,000) = (20,000-10,000) 2 / ((30,000-10,000)(25,000-10,000))
- P(X < 20,000 ドル) = 0.333
レストランの総売上高が 20,000 ドル未満である確率は0.333です。
レストランの平均予想売上はいくらですか?
前に示した平均の公式を使用して、予想される平均売上を計算できます。
- 平均 = (a + b + c) / 3
- 平均 = (10,000 ドル + 30,000 ドル + 25,000 ドル) / 3
- 平均 = 21,667 ドル
平均予想販売数は21,667です。
追加リソース
次のチュートリアルでは、他の一般的に使用されるディストリビューションの紹介を提供します。