サンプルサイズが等しくない場合に t 検定を実行する方法

統計に関して学生がよく尋ねる質問は次のとおりです。

各グループのサンプルサイズが等しくない場合に t 検定を実行することはできますか?

短い答え:

はい、サンプルサイズが等しくない場合でも t 検定を実行できます。サンプルサイズが等しいことは、t 検定で行われる仮定の 1 つではありません。

本当の問題は、2 つのサンプルの分散が等しくない場合に発生します。これは、t 検定で行われる仮定の 1 つです。

これが発生した場合は、代わりに等分散を仮定しないウェルチの t 検定を使用することをお勧めします。

次の例は、分散が等しい場合とそうでない場合に、異なるサンプル サイズで T 検定を実行する方法を示しています。

例 1: 不等サンプルサイズと等分散

学生が特定の試験でより良い成績を収められるように設計された 2 つのプログラムを管理するとします。

結果は次のとおりです。

プログラム 1:

• n (サンプルサイズ): 500
• x (サンプル平均): 80
• s (サンプル標準偏差): 5

プログラム 2:

• n (サンプルサイズ): 20
• x (サンプル平均): 85
• s (サンプル標準偏差): 5

次のコードは、R で箱ひげ図を作成して各プログラムの試験得点の分布を視覚化する方法を示しています。

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

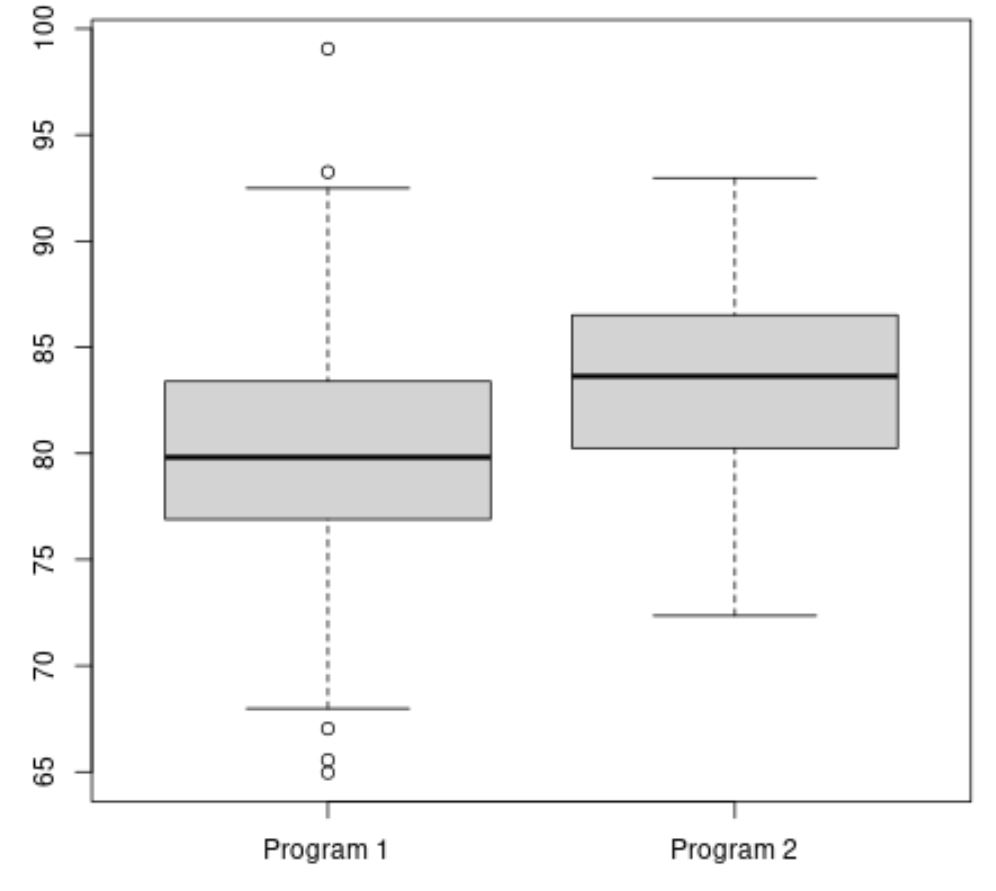
プログラム 2 の平均試験スコアはより高いように見えますが、2 つのプログラム間の試験スコアの分散はほぼ等しいです。

次のコードは、ウェルチの t 検定を使用して独立サンプルの t 検定を実行する方法を示しています。

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

独立サンプルの t 検定は p 値0.0009を返し、ウェルチの t 検定は p 値0.0029を返します。

各検定の p 値は 0.05 未満であるため、各検定の帰無仮説は棄却され、2 つのプログラム間の試験の平均得点には統計的に有意な差があると結論付けることになります。

サンプル サイズが等しくなくても、2 つのサンプルの分散が等しいため、独立サンプルの t 検定とウェルチの t 検定はどちらも同様の結果を返します。

例 2: 不等なサンプルサイズと不等な分散

学生が特定の試験でより良い成績を収められるように設計された 2 つのプログラムを管理するとします。

結果は次のとおりです。

プログラム 1:

• n (サンプルサイズ): 500
• x (サンプル平均): 80
• s (サンプル標準偏差): 25

プログラム 2:

• n (サンプルサイズ): 20
• x (サンプル平均): 85
• s (サンプル標準偏差): 5

次のコードは、R で箱ひげ図を作成して各プログラムの試験得点の分布を視覚化する方法を示しています。

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

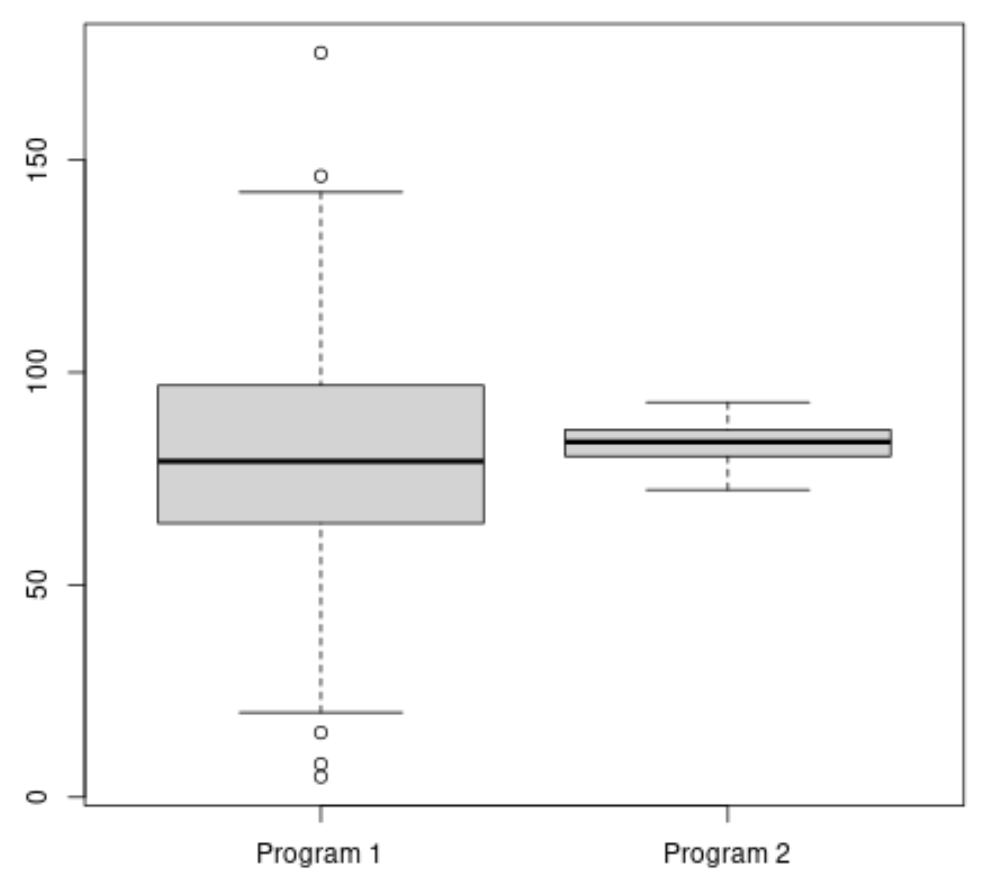
プログラム 2 の平均試験スコアはより高いように見えますが、プログラム 1 の試験スコアの分散はプログラム 2 よりもはるかに高くなっています。

次のコードは、ウェルチの t 検定を使用して独立サンプルの t 検定を実行する方法を示しています。

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

独立サンプルの t 検定は0.5496の p 値を返し、ウェルチの t 検定は0.0361の p 値を返します。

独立サンプルの t 検定では、試験の平均点の差を検出できませんが、ウェルチの t 検定では統計的に有意な差を検出できます。

2 つのサンプルの分散が等しくないため、ウェルチの t 検定だけが平均試験得点の統計的に有意な差を検出できました。この検定はサンプル間の分散が等しいと仮定していないためです。

追加リソース

次のチュートリアルでは、t 検定に関する追加情報を提供します。

1 サンプル t 検定の概要
2 標本 t 検定の概要
対応のあるサンプルの t 検定の概要