Excel で中心極限定理を適用する方法
中心極限定理は、たとえ母集団の分布が正規でなくても、サンプルサイズが十分に大きければ標本平均の標本分布はほぼ正規になるということです。
中心極限定理は、標本分布が次の特性を持つことも示しています。
1.標本分布の平均は母集団分布の平均と等しくなります。
x = μ
2.標本分布の標準偏差は、母集団の標準偏差を標本サイズで割ったものとなります。
s = σ / √n
このチュートリアルでは、Excel で中心極限定理を特定の分布に適用する方法を説明します。
Excel での中心極限定理の適用
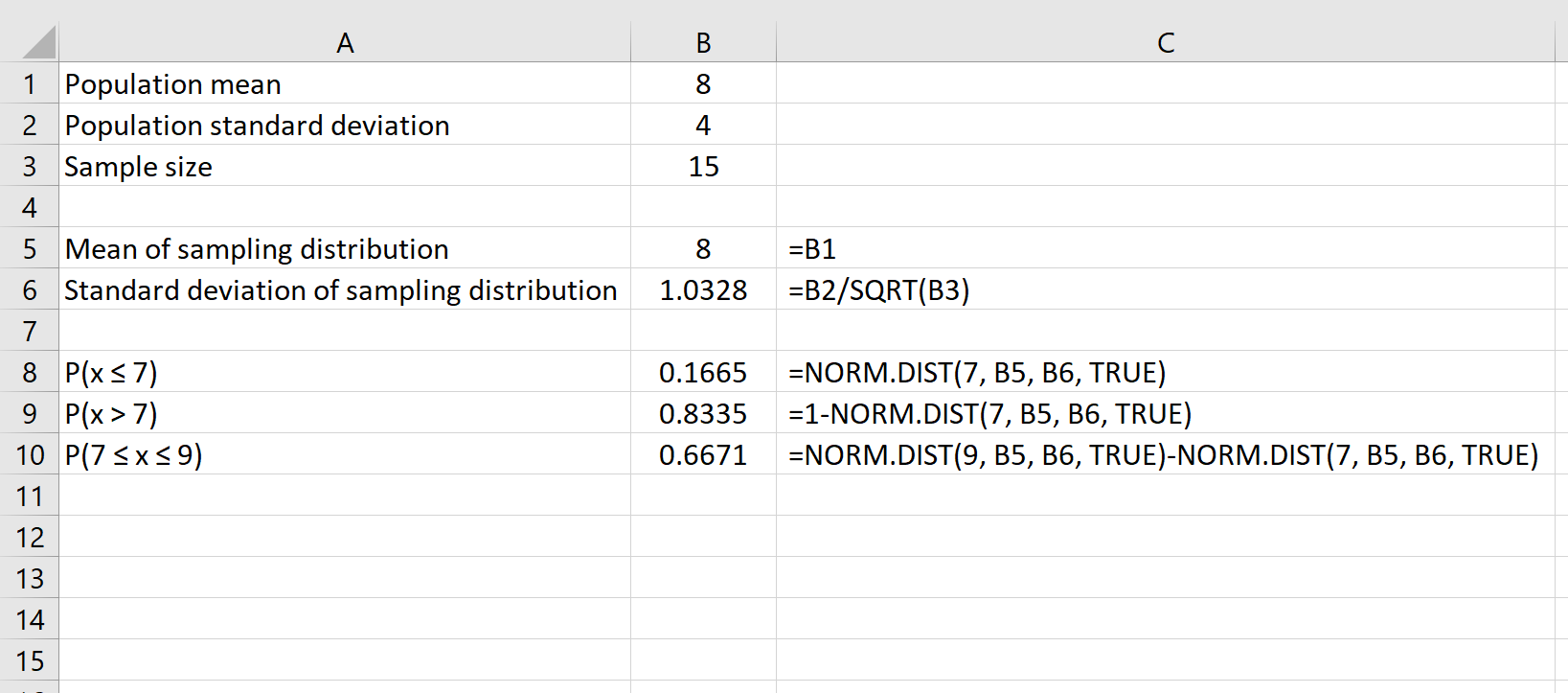
平均が8 、標準偏差が4の分布があるとします。 Excel で次の数式を使用すると、標本サイズ15の標本分布の平均と標準偏差の両方を求めることができます。
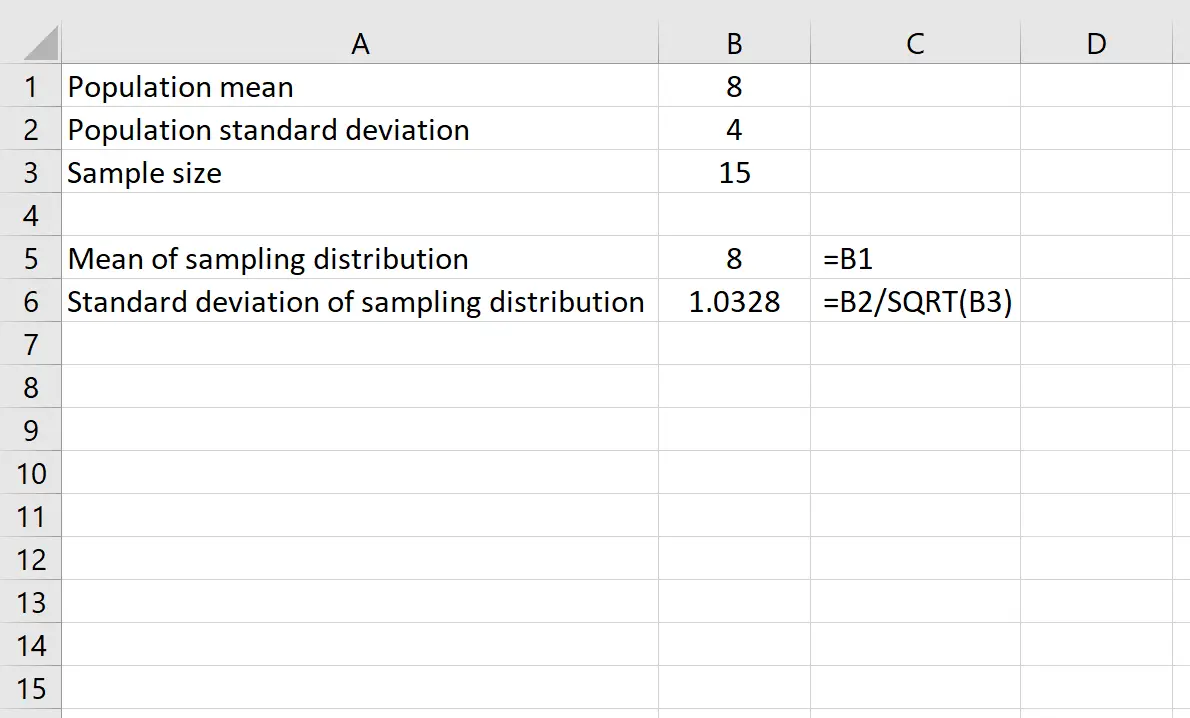
標本分布の平均値は母集団分布の平均値8に単純に等しくなります。
標本分布の標準偏差は、母集団の標準偏差を標本サイズで割った値、つまり 4 /√15 = 1.0328に等しくなります。
中心極限定理を使用して、確率に関する質問に答えることもできます。たとえば、特定の母集団の平均が8で標準偏差が4 の場合、サイズ15の特定のサンプルが存在する確率はいくらですか。 平均は7以下ですか?
この質問に答えるには、Excel でNORM.DIST()関数を使用します。この関数は次の構文を使用します。
NORM.DIST(x、平均、standard_dev、累積)
金:
- x:サンプルはテストすることを意味します
- 平均値:標本分布の期待平均値
- standard_dev:標本分布の期待される標準偏差
- 累積: TRUE は通常の CDF 値を返します。 FALSE は通常の PDF の値を返します。この場合、常に TRUE を使用します。
この関数は、サンプル平均が特定の値以下である確率を返します。
この例で使用する式は次のとおりです。
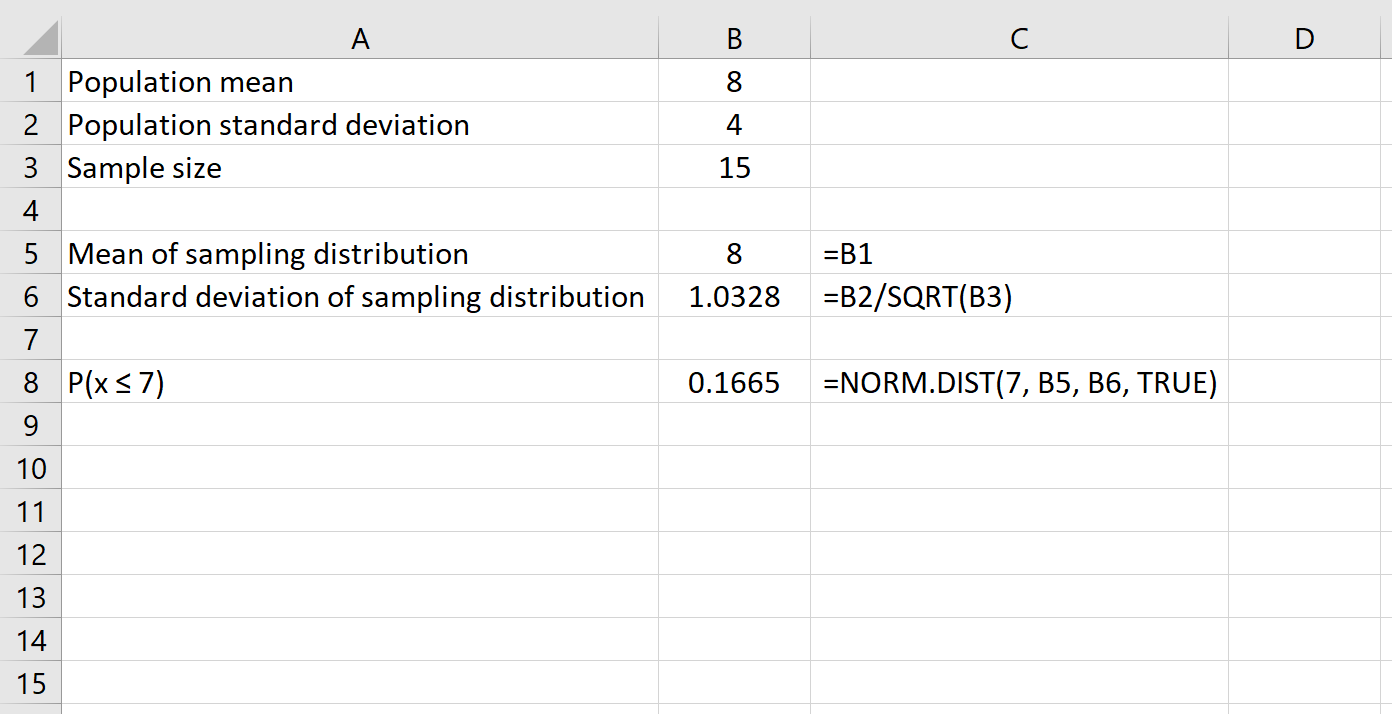
これは、平均が8で標準偏差が4 の母集団の場合、サイズ15の特定のサンプルが得られる確率が 平均は7または0.1665以下です。
また、式1 – NORM.DIST()を使用するだけで、特定のサンプル サイズの平均が特定の数値より大きくなる確率を求めることもできます。
たとえば、次の式は、指定されたサンプル サイズ 15 の平均値が 7を超える確率を決定する方法を示しています。
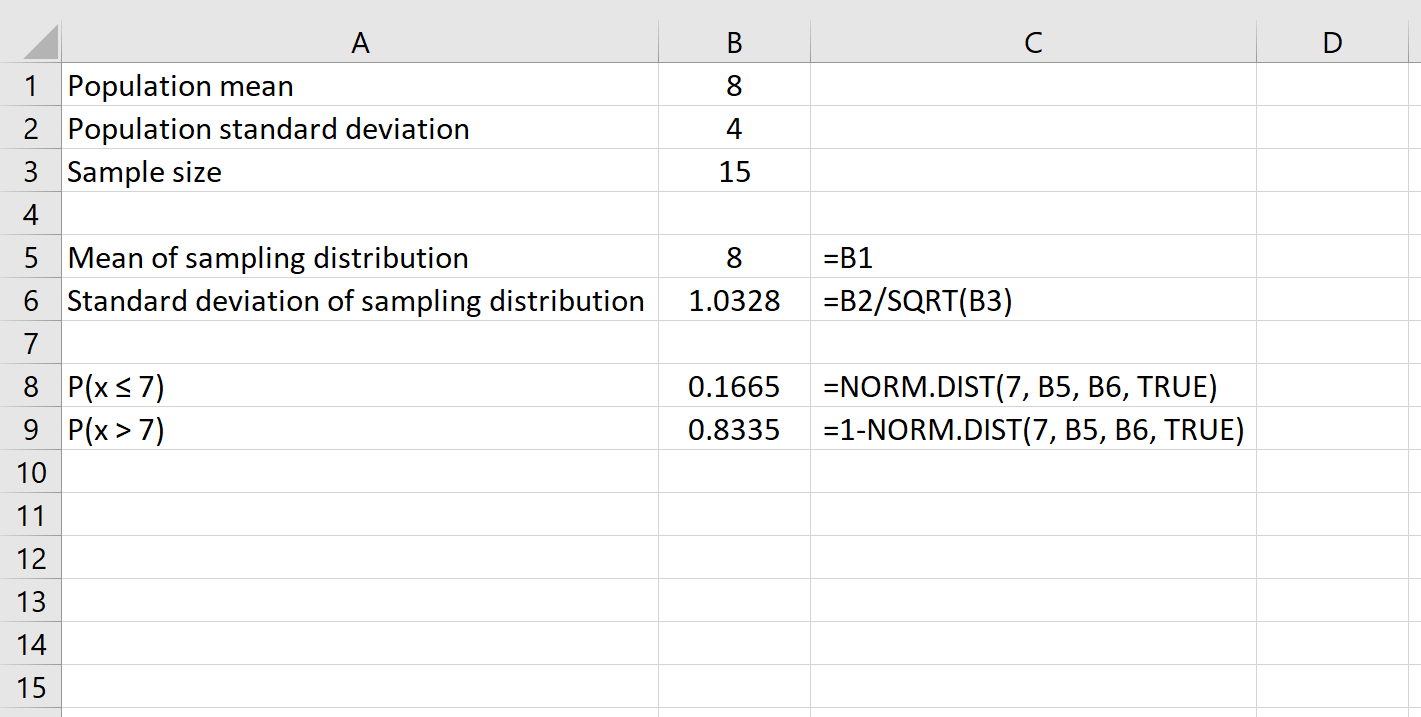
最後に、式NORM.DIST(大きい数値) – NORM.DIST(小さい数値)を使用して、指定されたサンプル サイズが 2 つの数値間の平均を持つ確率を求めることができます。
たとえば、次の式は、指定されたサンプル サイズ 15 の平均が 7 ~ 9 である確率を求める方法を示しています。