予測の妥当性とは何ですか? (定義と例)
統計学では、予測妥当性という用語は、将来の別の変数の値を予測するためにスケールまたはテストのスコアを使用することがどの程度有効であるかを指します。
たとえば、特定の大学の入学試験が生徒の第 1 学期の成績平均点をどの程度予測できるかを知りたい場合があります。
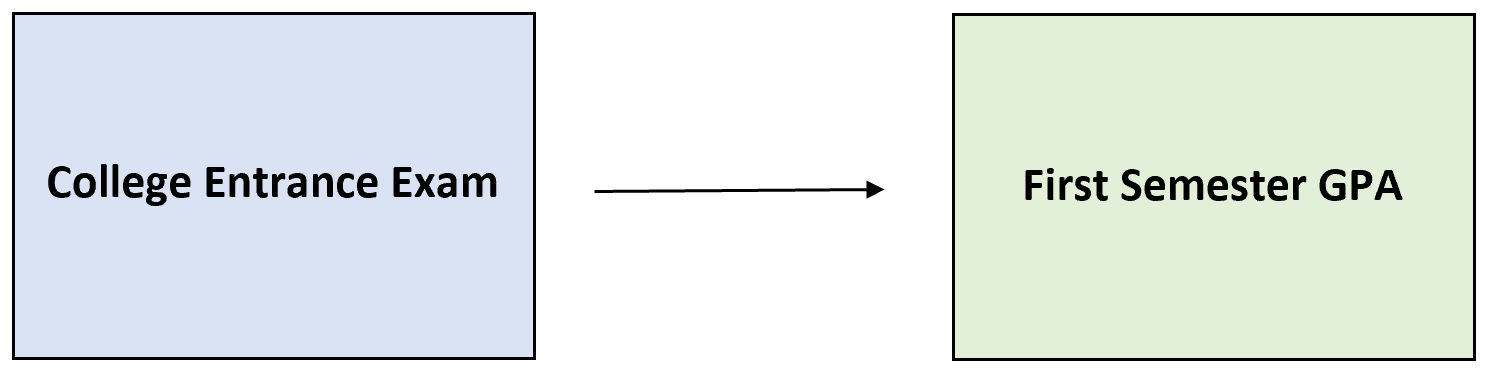
予測の妥当性が存在するかどうかを判断するには、次のプロセスを使用できます。
- 1,000 人の先輩に大学入学試験を実施します。
- 1 年後、同じ 1,000 人の学生の最初の学期の GPA に関するデータを収集します。
- 入学試験の得点と前期GPAの 相関を計算します。
入学試験の得点と最初の学期の GPA の間に強い相関関係がある場合、これら 2 つの変数の間に予測妥当性がある可能性があります。
言い換えれば、学生がこの大学入学試験で獲得した成績は、その学生が大学の最初の学期中に達成するであろう GPA を予測することになります。
たとえば、入学試験で高得点を獲得した生徒は、1 学期の得点も高くなる傾向があります。逆に、入学試験の成績が悪かった学生は、最初の学期の GPA が低い傾向があります。
技術的なメモ:
予測妥当性は基準妥当性の一種で、ある変数の測定値が別の変数の応答を予測する能力を指します。
一方の変数は説明変数と呼ばれ、もう一方の変数は応答変数または基準変数と呼ばれます。
前の例では、説明変数は入学試験、基準変数は最初の学期の GPA になります。
予測の妥当性の例
次の例は、予測の妥当性を計算できる追加のシナリオをいくつか示しています。
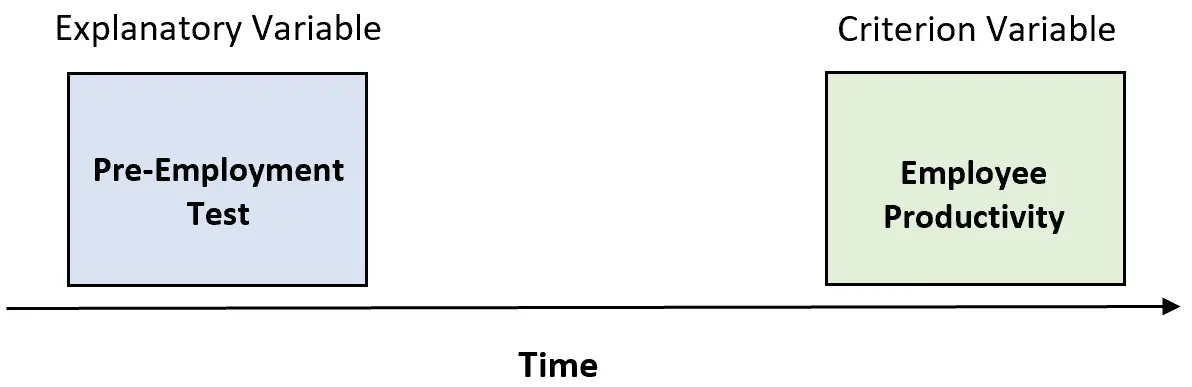
例 1: 採用前テスト
企業は、採用した全員に 40 問の採用前テストを実施し、1 年後に従業員の生産性を評価できます。
テスト結果と従業員の生産性の間に高い相関関係がある場合、テストを使用して個人の将来の生産性を予測することは有効であると言えます。
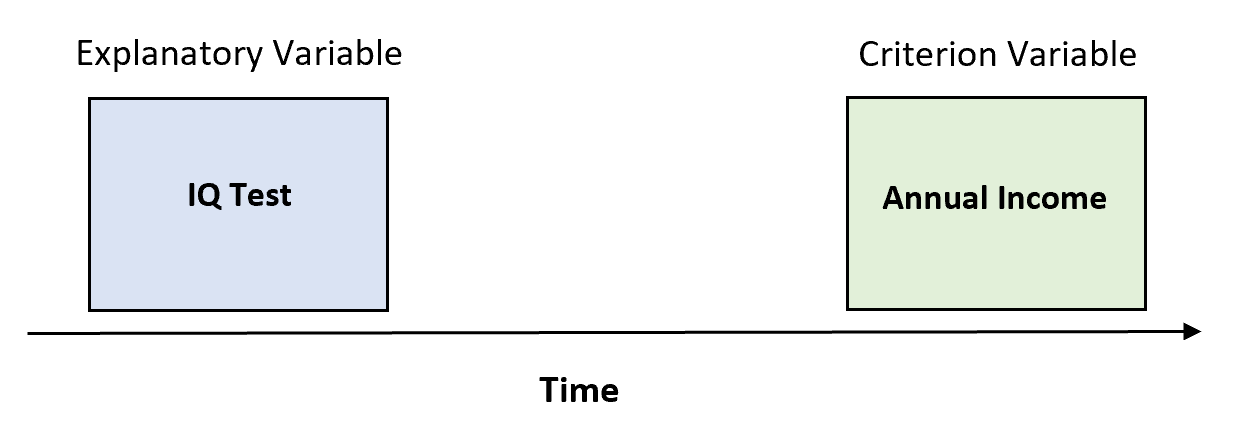
例 2: IQ テストと収入
研究者は 100 人に IQ テストを実施し、10 年後のそれらの人々の年収を追跡することができます。
IQ テストのスコアと個人の年収の間に高い相関関係がある場合、研究者は、このテストを個人の将来の収入を予測するために使用することが有効であると言えます。
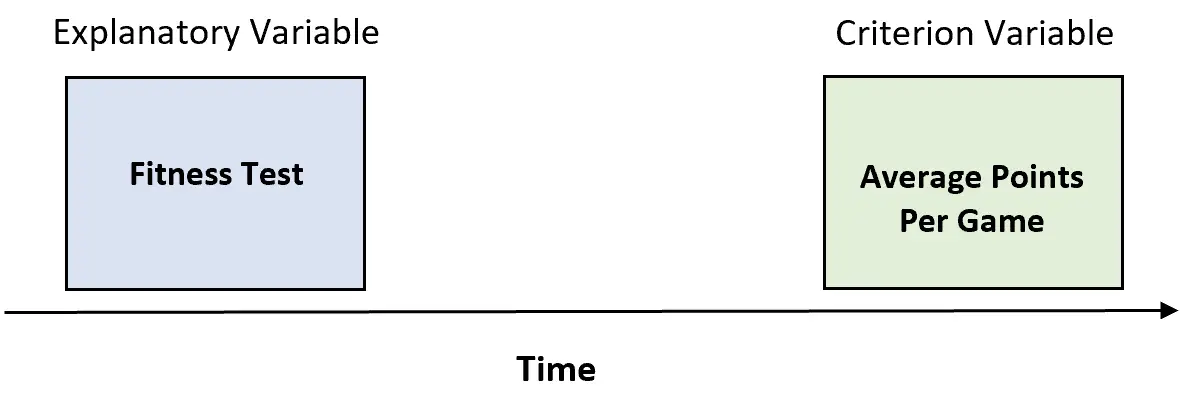
例 3: フィットネス
パーソナル トレーナーは、NBA ルーキーにフィットネス テストを実施し、リーグでの今後 5 年間に選手が獲得した 1 試合あたりの平均ポイントを記録できます。
フィットネス テストのスコアと、プレーヤーが獲得した 1 試合あたりの平均ポイントとの間に高い相関関係がある場合、パーソナル トレーナーは、プレーヤーの将来の 1 試合あたりのポイントを予測するためにテストを使用することが有効であると言うかもしれません。
予測の妥当性に関して高い相関があると考えられるのは何ですか?
2 つの変数間の「高い」相関関係とはみなされる特定の値はありません。ただし、テストと測定対象の構成要素との間の相関が高ければ高いほど、テストの予測妥当性も高くなります。
たとえば、採用前のテストと 1 年後の従業員の生産性との相関が0.86の場合、そのテストは相関が0.35しかないテストよりも従業員の生産性を予測します。
ただし、かなり低いと思われる相関関係 (r = 0.35 など) であっても、従業員の生産性の可能性について少なくともある程度のアイデアが得られるため、雇用主にとっては依然として有用です。