R で二次回帰を実行する方法
2 つの変数に線形関係がある場合、多くの場合、 単純な線形回帰を使用してそれらの関係を定量化できます。

ただし、2 つの変数に二次関係がある場合は、二次回帰を使用してそれらの関係を定量化できます。

このチュートリアルでは、R で 2 次回帰を実行する方法について説明します。
例: R の二次回帰
労働時間と報告された幸福度との関係を理解したいとします。 11 人の異なる人々の週の労働時間数と報告された幸福度 (0 から 100 のスケール) に関する次のデータがあります。

R で二次回帰モデルを近似するには、次の手順を使用します。
ステップ 1: データを入力します。
まず、データを含むデータ フレームを作成します。
#createdata data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60), happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27)) #viewdata data hours happiness 1 6 14 2 9 28 3 12 50 4 14 70 5 30 89 6 35 94 7 40 90 8 47 75 9 51 59 10 55 44 11 60 27
ステップ 2: データを視覚化します。
次に、データを視覚化するための単純な散布図を作成します。
#create scatterplot
plot(data$hours, data$happiness, pch=16)
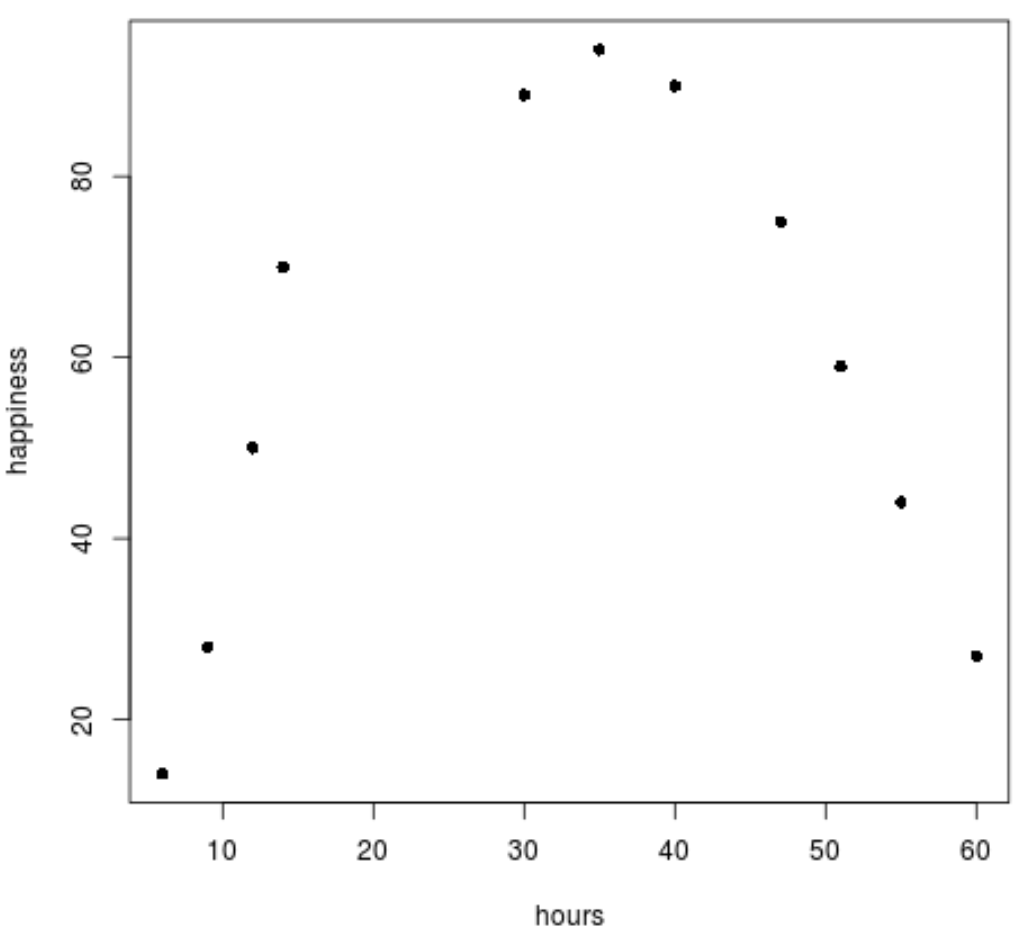
データが線形パターンに従っていないことがはっきりとわかります。
ステップ 3: 単純な線形回帰モデルを当てはめます。
次に、単純な線形回帰モデルを当てはめて、データにどの程度適合するかを確認します。
#fit linear model linearModel <- lm(happiness ~ hours, data=data) #view model summary summary(linearModel) Call: lm(formula = happiness ~ hours) Residuals: Min 1Q Median 3Q Max -39.34 -21.99 -2.03 23.50 35.11 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 48.4531 17.3288 2.796 0.0208 * hours 0.2981 0.4599 0.648 0.5331 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 28.72 on 9 degrees of freedom Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331
複数の R 二乗値で示されるように、モデルによって説明される幸福度の合計分散はわずか4.46%です。
ステップ 4: 二次回帰モデルを当てはめます。
次に、二次回帰モデルを当てはめます。
#create a new variable for hours 2 data$hours2 <- data$hours^2 #fit quadratic regression model quadraticModel <- lm(happiness ~ hours + hours2, data=data) #view model summary summary(quadraticModel) Call: lm(formula = happiness ~ hours + hours2, data = data) Residuals: Min 1Q Median 3Q Max -6.2484 -3.7429 -0.1812 1.1464 13.6678 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -18.25364 6.18507 -2.951 0.0184 * hours 6.74436 0.48551 13.891 6.98e-07 *** hours2 -0.10120 0.00746 -13.565 8.38e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6.218 on 8 degrees of freedom Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06
モデルによって説明される幸福度の合計分散は96.02%に増加しました。
次のコードを使用して、モデルがデータにどの程度適合しているかを視覚化できます。
#create sequence of hour values hourValues <- seq(0, 60, 0.1) #create list of predicted happiness levels using quadratic model happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2)) #create scatterplot of original data values plot(data$hours, data$happiness, pch=16) #add predicted lines based on quadratic regression model lines(hourValues, happinessPredict, col='blue')
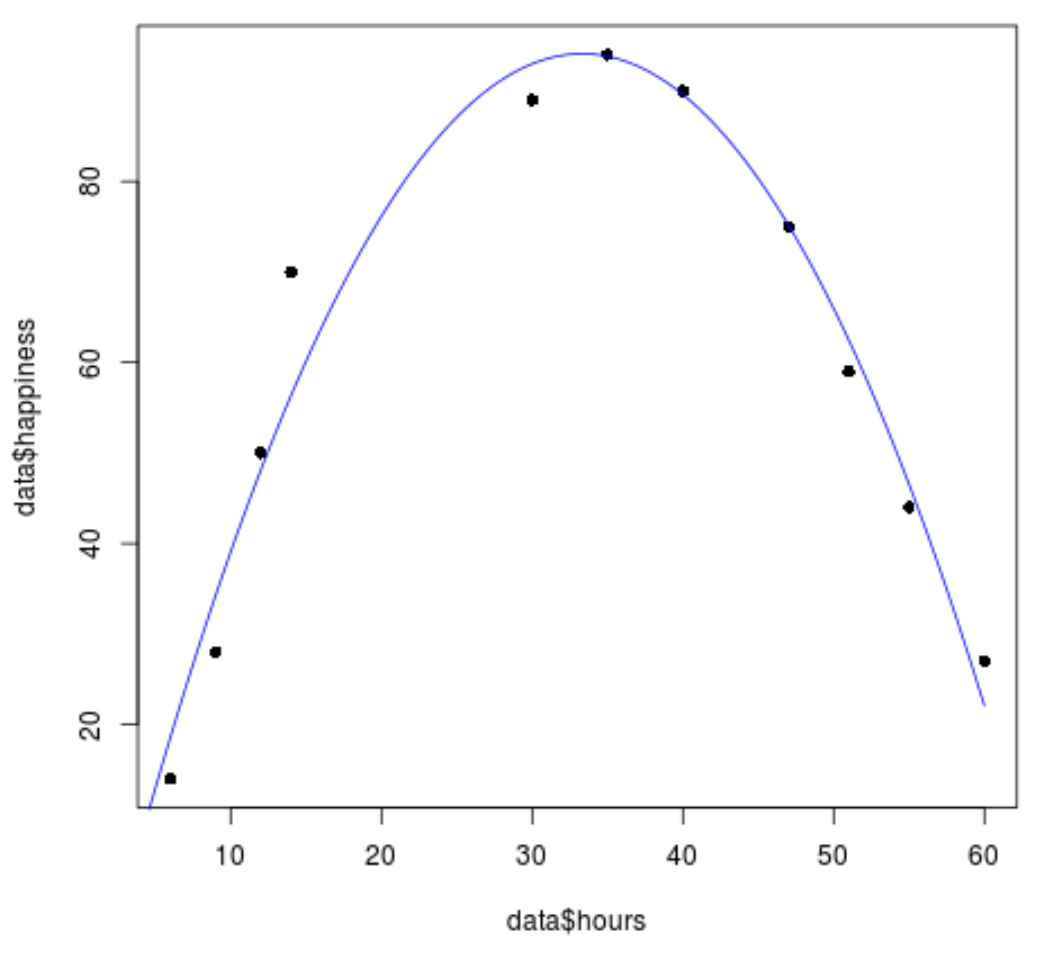
二次回帰直線がデータ値に非常によく適合していることがわかります。
ステップ 5: 二次回帰モデルを解釈します。
前のステップで、二次回帰モデルの結果が次のようになることを見ました。
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18.25364 6.18507 -2.951 0.0184 *
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
ここで示した係数に基づいて、調整された二次回帰は次のようになります。
幸福度 = -0.1012 (時間) 2 + 6.7444 (時間) – 18.2536
この方程式を使用すると、週あたりの労働時間を考慮した個人の予測幸福度を見つけることができます。
たとえば、週に 60 時間働く人の幸福度は22.09になります。
幸福度 = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09
逆に、週に 30 時間働く人の幸福度は92.99になるはずです。
幸福度 = -0.1012(30) 2 + 6.7444(30) – 18.2536 = 92.99