Python で二項分布を使用する方法

二項分布は、統計で最もよく使用される分布の 1 つです。これは、 n回の二項実験でk 回の成功が得られる確率を表します。

確率変数X が二項分布に従う場合、 X = kが成功する確率は次の式で求められます。

P(X=k) = _n C _k * p ^k * (1-p) ^nk

金：

• n:試行回数
• k:成功回数
• p:与えられた試行の成功確率
• _n C _k : n回の試行でk 個の成功を得る方法の数

このチュートリアルでは、Python で二項分布を使用する方法を説明します。

二項分布を生成する方法

numpy ライブラリのrandom.binomial関数を使用して、二項分布に従う値の配列を生成できます。

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

結果として得られる表の各数値は、 10回の試行中に遭遇した「成功」の数を表します。ここで、特定の試行における成功の確率は0.25でした。

二項分布を使用して確率を計算する方法

scipy ライブラリのbinom 関数を使用して、二項確率に関する質問に答えることもできます。

質問 1:ネイサンはフリースロー試投の 60% を成功させます。彼がフリースローを 12 回成功させた場合、ちょうど 10 回成功する確率はどれくらいですか?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

ネイサンがちょうど 10 本のフリースローを成功させる確率は0.0639です。

質問 2:マーティは公正なコインを 5 回投げます。コインの表が 2 回以下になる確率はいくらですか?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

コインが 2 回以下で表になる確率は0.5です。

質問 3:個人の 70% が特定の法律を支持していることはわかっています。 10 人が無作為に選ばれた場合、そのうち 4 人から 6 人が法律を支持する確率はどれくらいですか?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

ランダムに選択された 4 ～ 6 人の個人が法則を支持する確率は0.3398です。

二項分布を視覚化する方法

seabornライブラリとmatplotlibライブラリを使用して、Python で二項分布を視覚化できます。

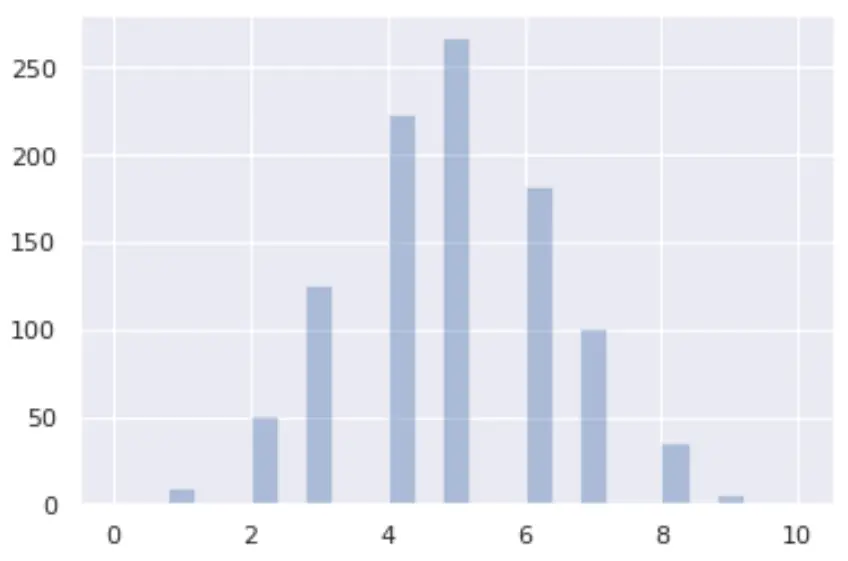
 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

お茶