二項分布の形状を理解する
二項分布は、 n回の二項実験でk回の成功が得られる確率を表します。
確率変数X が二項分布に従う場合、 X = kが成功する確率は次の式で求められます。
P(X=k) = n C k * p k * (1-p) nk
金:
- n:試行回数
- k:成功回数
- p:与えられた試行の成功確率
- n C k : n回の試行でk 個の成功を得る方法の数
次の 2 つの条件のうち 1 つ以上が発生すると、二項確率分布は釣鐘型になる傾向があります。
1.サンプルサイズ (n) が大きい。
2.特定の試行の成功確率 (p) は 0.5 に近いです。
ただし、これらの条件がどちらも発生しない場合、二項確率分布は歪む傾向があります。これを説明するために、次の例を考えてみましょう。
例 1: サンプル サイズ (n) が大きい
次のグラフは、 n = 200および p = 0.5の場合の確率分布を示します。
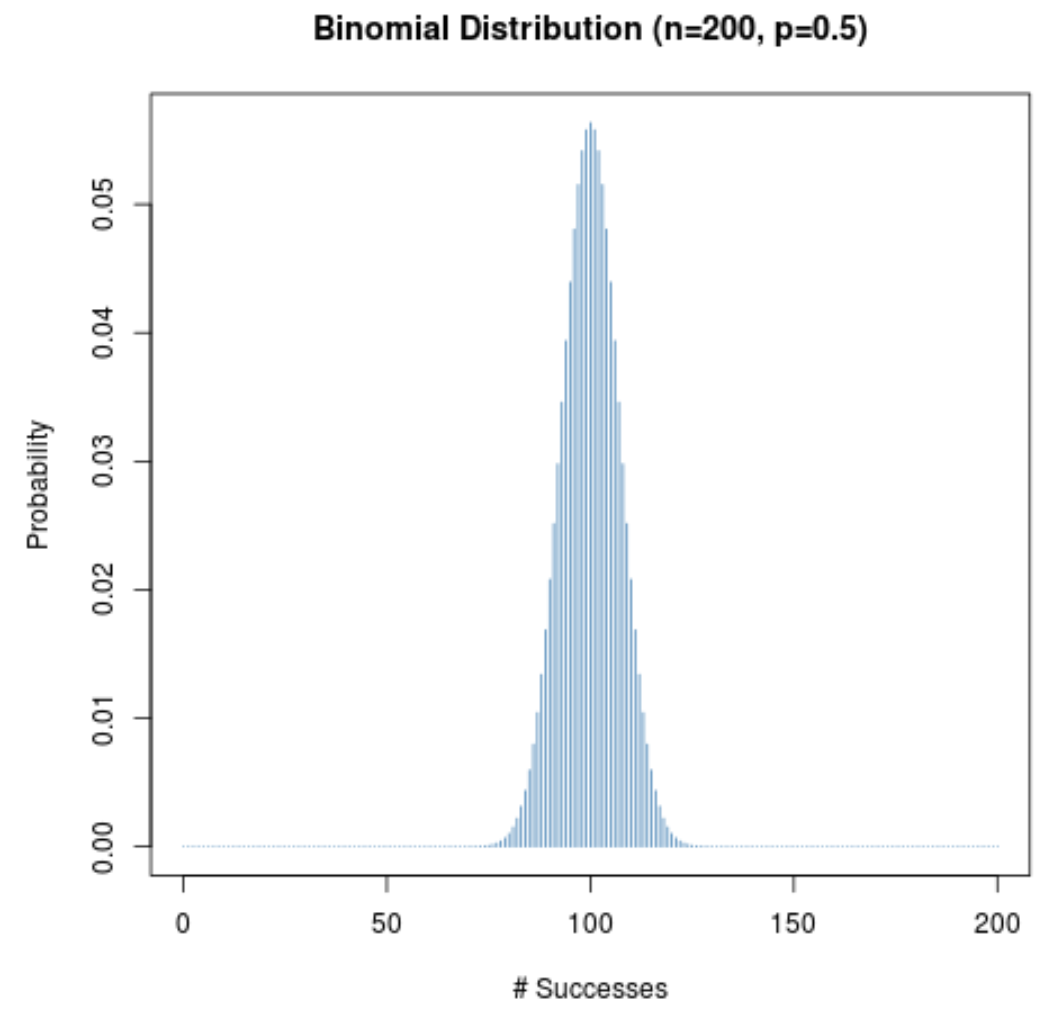
X 軸は 200 回の試行にわたる成功数を表示し、Y 軸はその数の成功が発生する確率を表示します。
(1)サンプルサイズが大きく、 (2)特定の試行の成功確率が 0.5 に近いため、確率分布は釣鐘型になります。
特定の試行の成功確率 (p) が 0.5 に近くない場合でも、サンプル サイズ (n) が大きい限り、確率分布は釣鐘型のままになります。これを説明するために、p = 0.2 および p = 0.8 の場合の次の 2 つのシナリオを考えてみましょう。
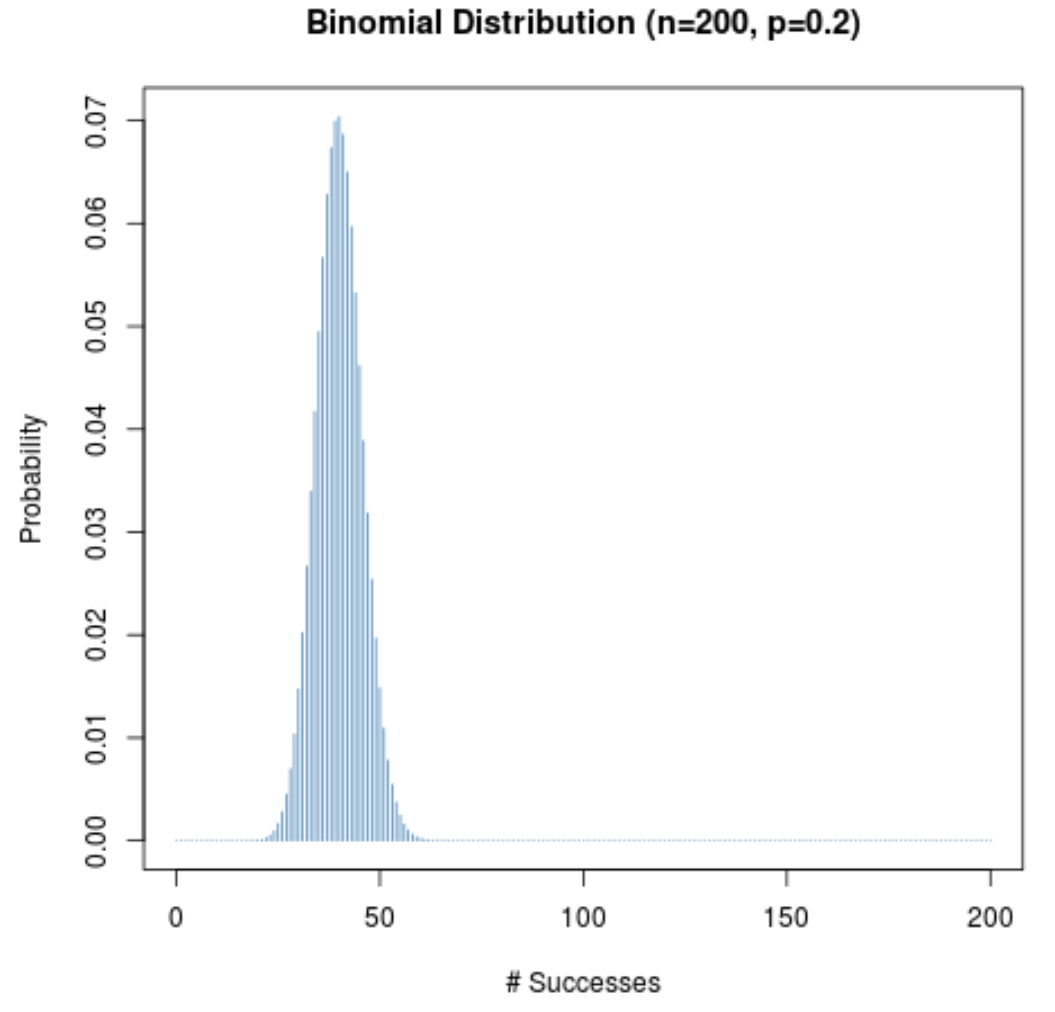
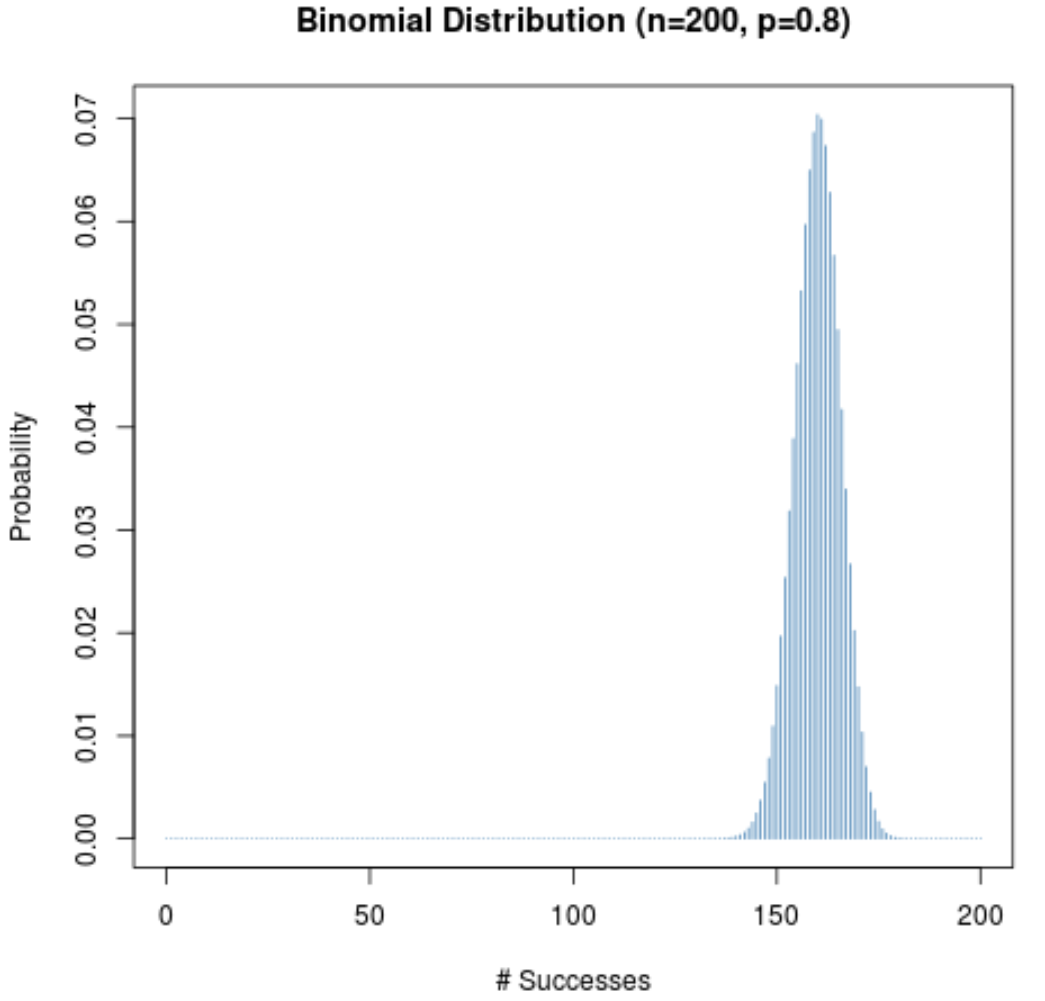
どちらのシナリオでも確率分布が釣鐘型になっていることに注目してください。
例 2: 成功の確率 (p) は 0.5 に近い
次のグラフは、 n = 10および p = 0.4の場合の確率分布を示します。
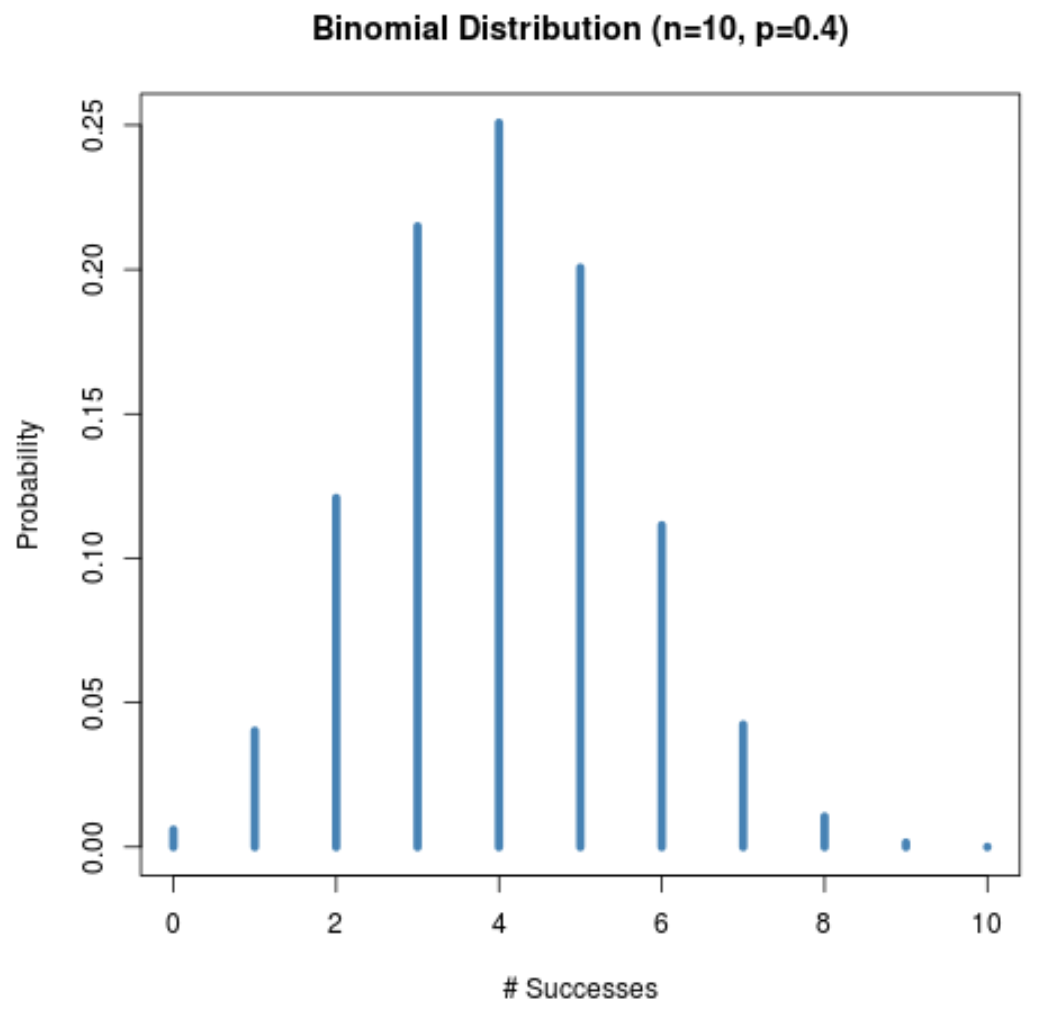
サンプルサイズ (n = 10) は小さいですが、特定の試行の成功確率 (p = 0.4) が 0.5 に近いため、確率分布は釣鐘型のままです。
例 3: 歪んだ二項分布
(1)サンプルサイズが大きくなく、 (2)特定の試行の成功確率が 0.5 に近くない場合、二項確率分布は左または右に偏ります。
たとえば、次のグラフは、 n = 20および p = 0.1の場合の確率分布を示します。
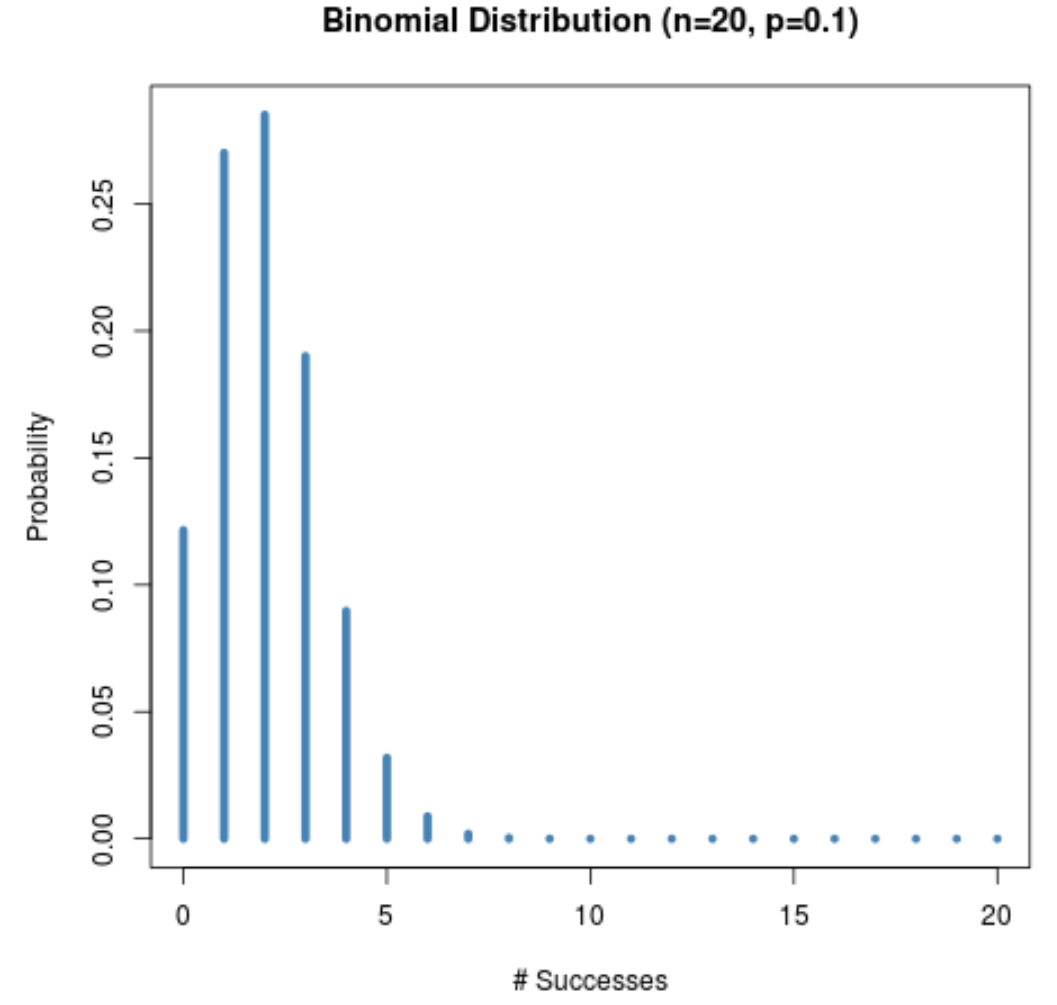
分布が右に偏っていることに注目してください。
そして、次のグラフは、n = 20 、p = 0.9の場合の確率分布を示しています。
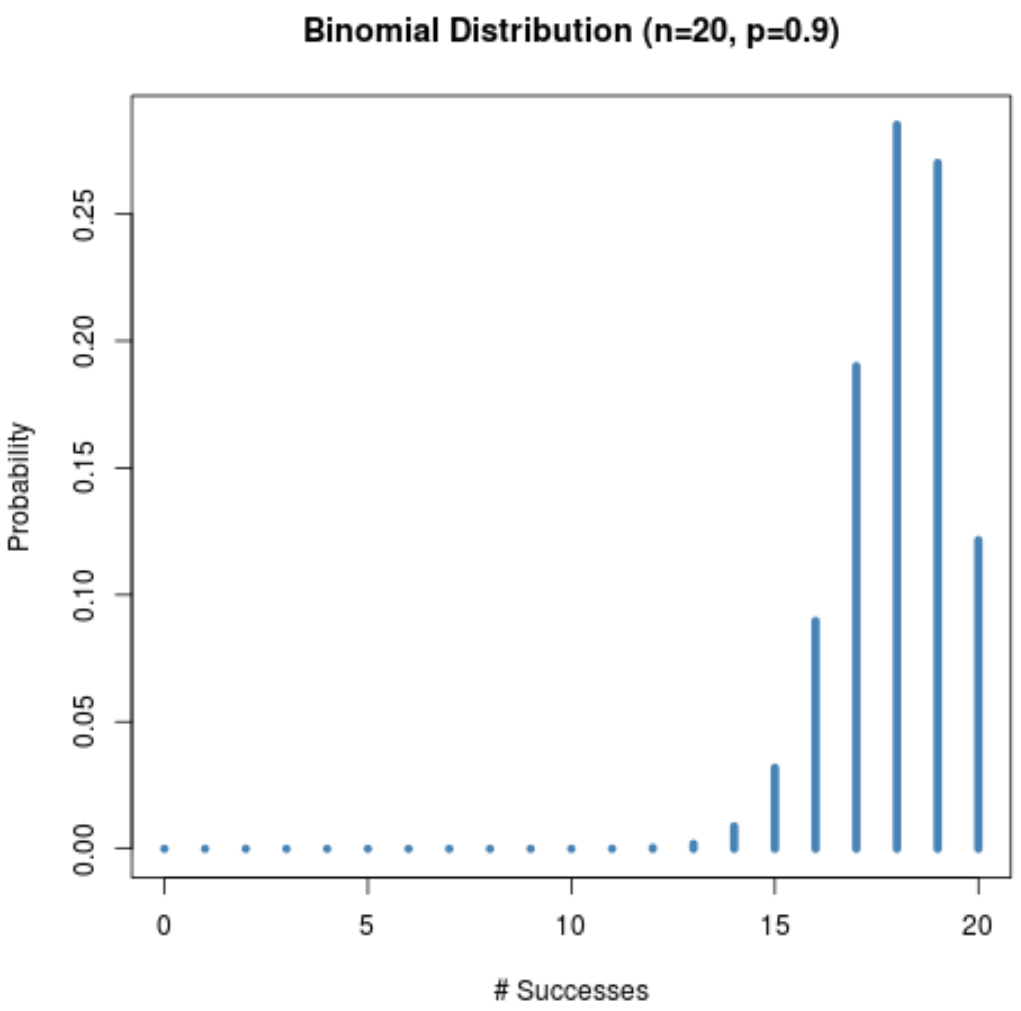
分布が左に偏っていることに注目してください。
文末脚注
この記事の各グラフは、R 統計プログラミング言語を使用して作成されました。 このチュートリアルを使用して、R で独自の二項確率分布をプロットする方法を学びます。