二項分布表の読み方

二項分布表 は、二項分布に関連付けられた確率を示す表です。二項分布表を使用するには、次の 3 つの値のみが必要です。

• n:試行回数
• r: n 回の試行中の「成功」の数
• p:特定の試行が成功する確率

これら 3 つの数値を使用すると、二項分布表を使用して、各試行の成功確率がpの場合に、 n 回の試行中に正確にr回の成功が得られる確率を見つけることができます。

次の例は、二項分布テーブルを読み取る方法を示しています。

例1

質問:ジェシカはフリースロー試投の 60% を成功させます。彼女がフリースローを 6 回成功させた場合、ちょうど 4 回成功する確率はどれくらいですか?

この質問に答えるには、n = 6、 r = 4、およびp = 0.60に対応する二項分布表の値を見つけることができます。

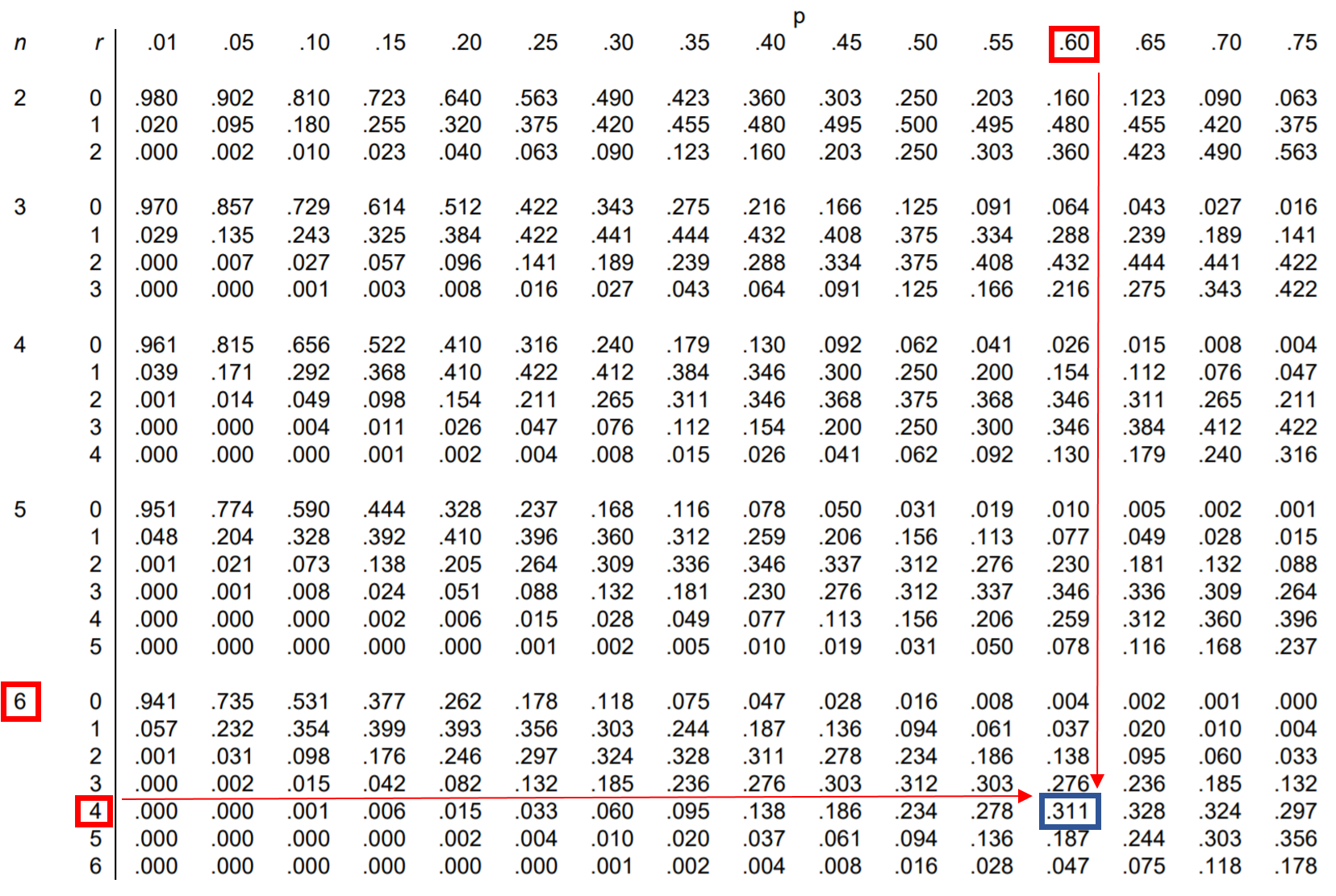
ジェシカがフリースロー 6 回中 4 回を正確に成功させる確率は0.311です。

例 2

質問:ジェシカはフリースロー試投の 60% を成功させます。彼女がフリースローを 6 回成功させた場合、彼女が成功させるのが 4 回未満になる確率はどれくらいですか?

この確率を見つけるには、実際に次の確率を追加する必要があります。

P(4 未満になる) = P(0 になる) + P(1 になる) + P(2 になる) + P(3 になる)

したがって、二項分布表でこれら 4 つの確率をそれぞれ検索し、それらを加算することができます。

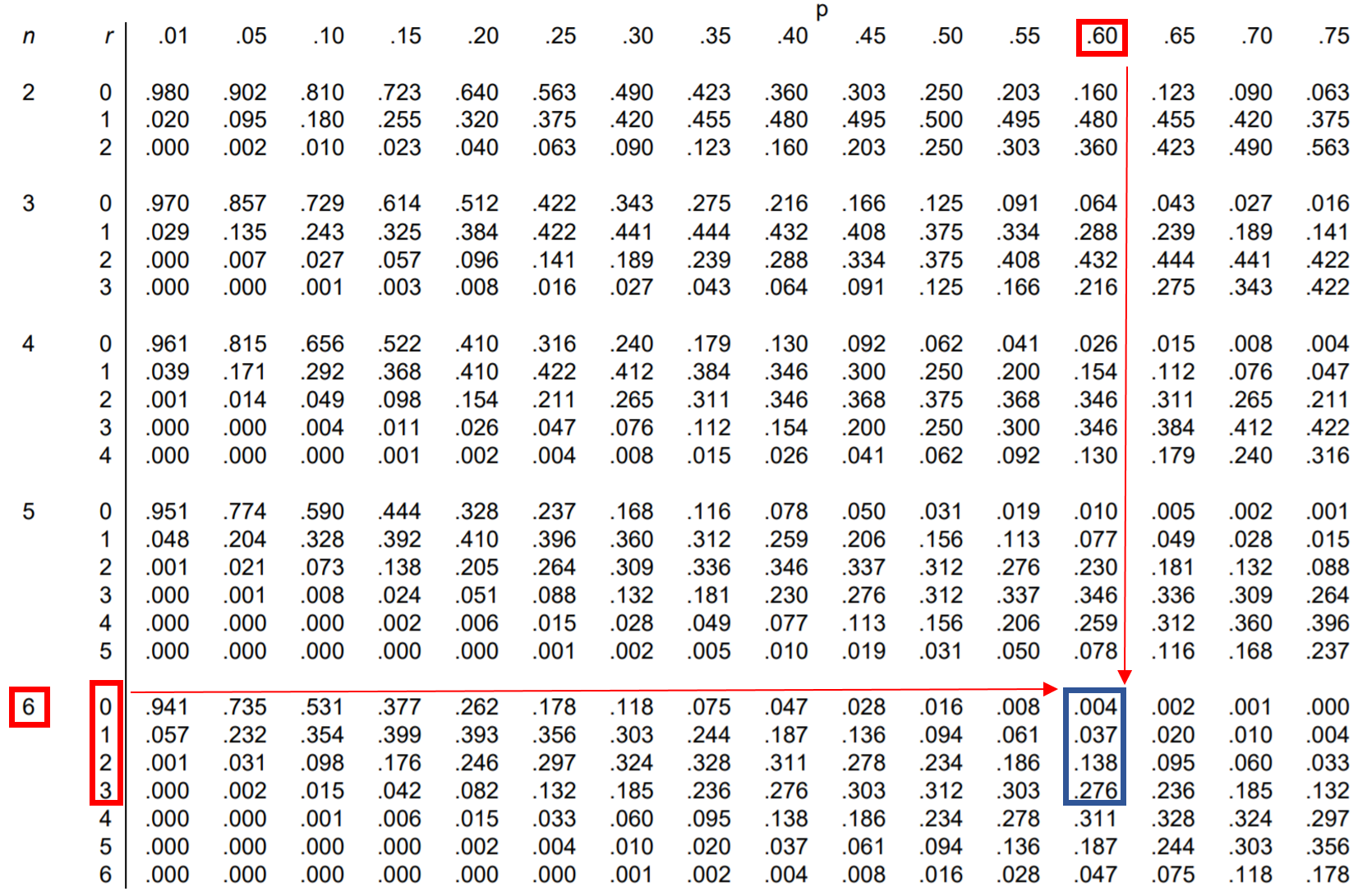
表から、P(4 未満) = .004 + .037 + .138 + .276 = 0.455となります。

ジェシカがフリースローを 4 回未満しか成功させない確率は0.455です。

例 3

質問:ジェシカはフリースロー試投の 60% を成功させます。彼女がフリースローを 6 本成功させた場合、彼女が 4 本以上を成功させる確率はどれくらいですか?

この確率を見つけるには、次の確率を追加する必要があります。

P(4つ以上作る) = P(4つ作る) + P(5つ作る) + P(6つ作る)

したがって、二項分布表でこれら 3 つの確率をそれぞれ検索し、それらを加算することができます。

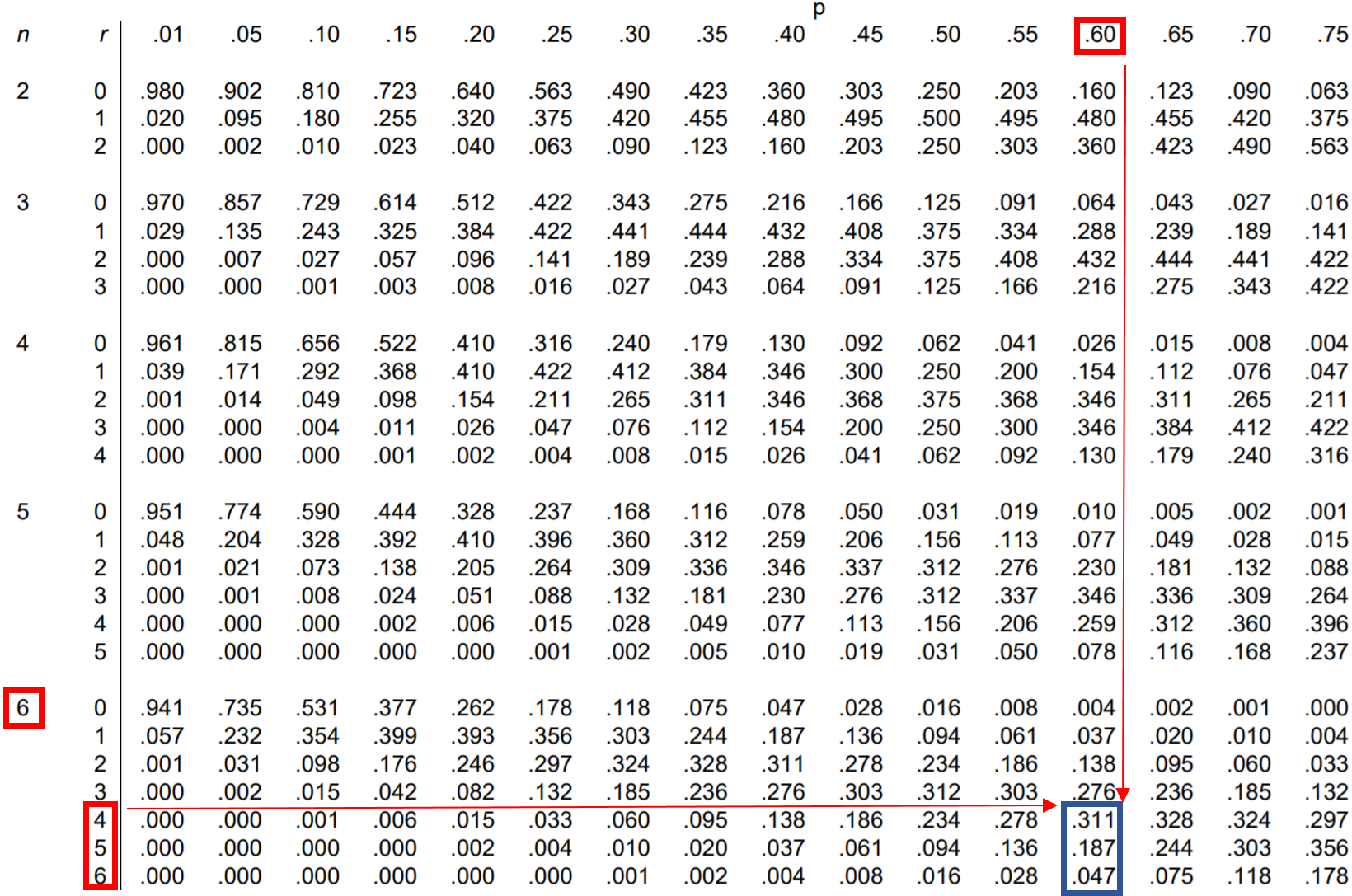
表より、P(4 以上になる) = .311 + .187 + .047 = 0.545となります。

ジェシカが 4 本以上のフリースローを成功させる確率は0.545です。