共分散

この記事では、共分散とは何か、またその計算方法について説明します。共分散の式とデータセットの共分散の計算例が見つかります。さらに、最後にオンライン計算機を使用して、任意のデータ系列の共分散を計算できます。

共分散とは何ですか?

統計学における共分散は、2 つの確率変数の共同変動の程度を示す値です。言い換えれば、共分散は 2 つの変数間の依存関係を分析するために使用されます。

共分散は、2 つの変数のデータとそれぞれの平均の差の積の合計をデータの総数で割ったものに等しくなります。

👉以下の計算機を使用して、任意のデータセットの共分散を計算できます。

共分散値の解釈は非常に簡単です。

• 共分散が正の場合、2 つの変数間に依存関係があることを意味します。したがって、1 つの変数の値が増加すると、他の変数も増加し、その逆も同様です。
• 共分散が負の場合、2 つの変数間の関係が負であることを意味します。したがって、1 つの変数の値が増加すると、もう 1 つの変数の値が減少し、その逆も同様です。
• 共分散がゼロ(またはその値がゼロに近い) の場合、これは 2 つの変数間に関係がないことを意味します。言い換えれば、2 つの確率変数は独立しています。

共分散の計算方法

データ系列の共分散を計算するには、次の手順を実行する必要があります。

1. 各変数の平均を個別に計算します。
2. 各変数について、その各値と変数の平均の差を見つけます。
3. 各データ ポイントについて、前の手順で計算された差を乗算します。
4. 前のステップで得られたすべての結果を合計します。
5. データの総数で割ります。得られた値はデータ系列の共分散です。

要約すると、2 つの変数間の共分散を計算する式は次のとおりです。

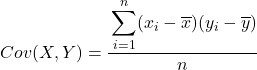
2 つの変数間の共分散を抽出するための強く推奨される方法は、すべてのデータ ペアを含むテーブルを作成し、上で説明した各手順に列を追加することです。こうすることで、計算がより整理され、何をしているのかをよりよく理解できるようになります。

共分散計算の例

共分散の定義を考慮して、このタイプの統計的尺度を計算する段階的な例を以下に示します。目的は、共分散の概念と 2 つの変数間の相関関係を分析する方法をより深く理解することです。

• 次の統計データ セットの共分散を計算します。

まず、各変数の算術平均を計算する必要があります。これを行うには、各変数の値の合計をデータの総数で割ります。

各確率変数の平均を決定したら、次の列をデータ テーブルに追加して共分散を取得できます。

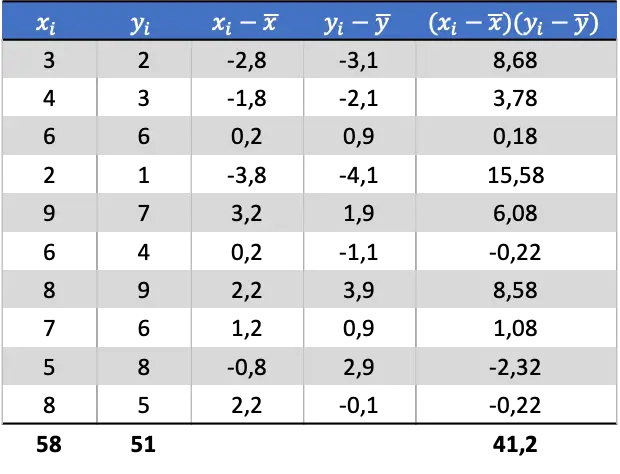
したがって、2 つの変数の共分散を求めるには、最後の列の合計をデータ ペアの数で割る必要があります。

この場合、共分散値は正であり、調査された 2 つの確率変数間に直接的な依存関係があることを意味します。ただし、共分散値が負であった場合、これは 2 つの変数間の依存関係が逆であることを意味します。最後に、共分散値がゼロまたはゼロに非常に近い場合は、2 つの変数間に線形関係がないことを意味します。

この例を解くとわかるように、Excel などのコンピューター プログラムを使用してテーブルに列を追加し、計算をすばやく実行すると非常に便利です。それ以外の場合、操作を手動で計算すると、共分散を見つけるのに非常に長い時間がかかります。

共分散計算機

一連の統計データを次の計算機に入力して、2 つの変数間の共分散を計算します。最初のボックスには 1 つの変数の値のみが含まれ、2 番目のボックスには 2 番目の変数の値のみが含まれるように、データのペアを分離する必要があります。

データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

共分散特性

共分散には次の特性があります。

• 確率変数と定数の間の共分散はゼロです。

• 変数とそれ自体の共分散は、その変数の分散と等価です。

• 共分散は対称性を満たしているため、変数 X と Y の共分散は変数 Y と X の共分散と等しくなります。変数の順序は共分散の結果に影響しません。

• 変数に定数を乗算する場合は、最初に共分散を計算してから、その結果に定数を乗算します。

• 変数に項を追加しても、共分散の結果には影響しません。

• 2 つの確率変数間の共分散は、それらの数学的期待値に関連しています。変数 X と Y の間の共分散は、X と Y の積の数学的期待値から各変数の数学的期待値の積を引いたものに等しくなります。

• 変数を操作する場合、共分散に関して次の代数式が満たされます。