Google スプレッドシートで共分散行列を作成する方法

共分散は、 1 つの変数の変化が 2 番目の変数の変化とどのように関連しているかを示す尺度です。より具体的には、これは 2 つの変数が線形に関連している程度の尺度です。

2 つの変数XとYの間の共分散を計算する式は次のとおりです。

COV( X , Y ) = Σ(x- x )(y- y ) / n

共分散行列は、多くの異なる変数間の共分散を示す正方行列です。これは、データ セット内でさまざまな変数がどのように関連しているかを理解するのに役立ちます。

次の例は、Google スプレッドシートで特定のデータセットの共分散行列を作成する方法を示しています。

Google スプレッドシートで共分散行列を作成する方法

数学、科学、歴史の 3 科目における 10 人の異なる生徒のテストのスコアを示す次のデータセットがあるとします。

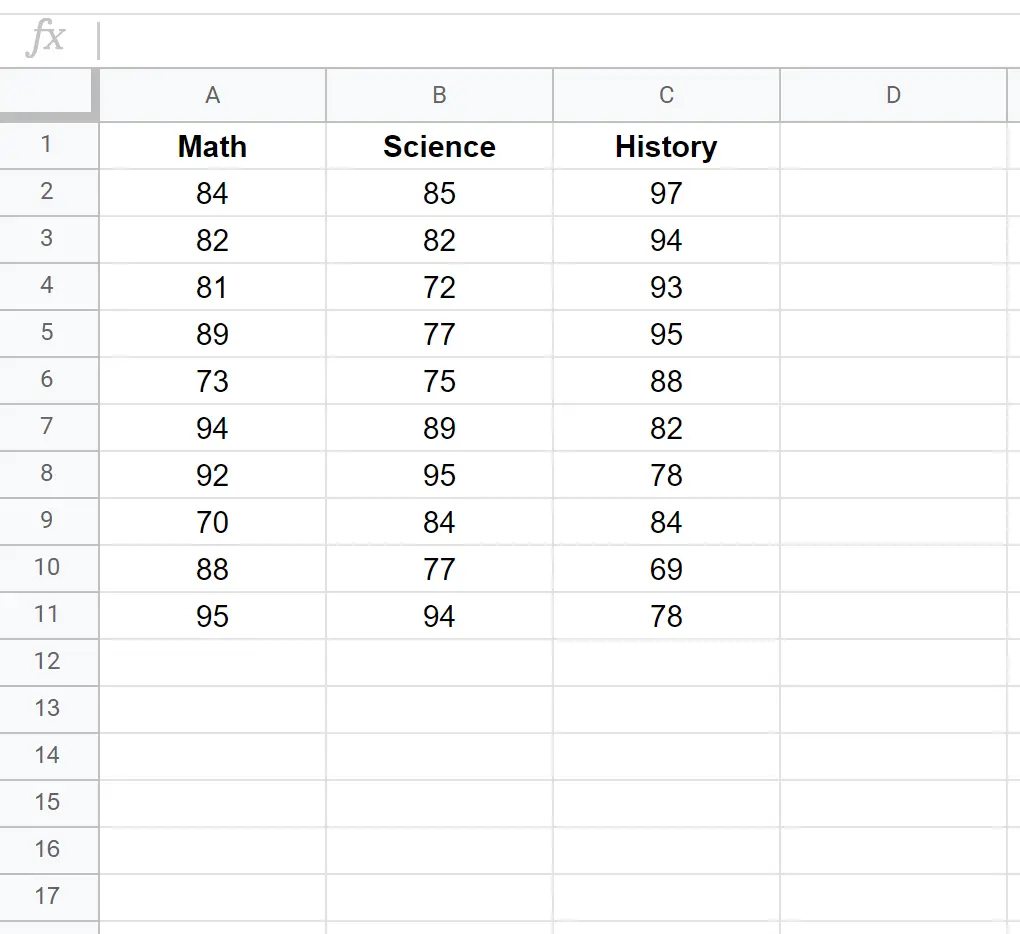
このデータセットの共分散行列を作成するには、次の構文でCOVAR()関数を使用します。

COVAR(データ_y, データ_x)

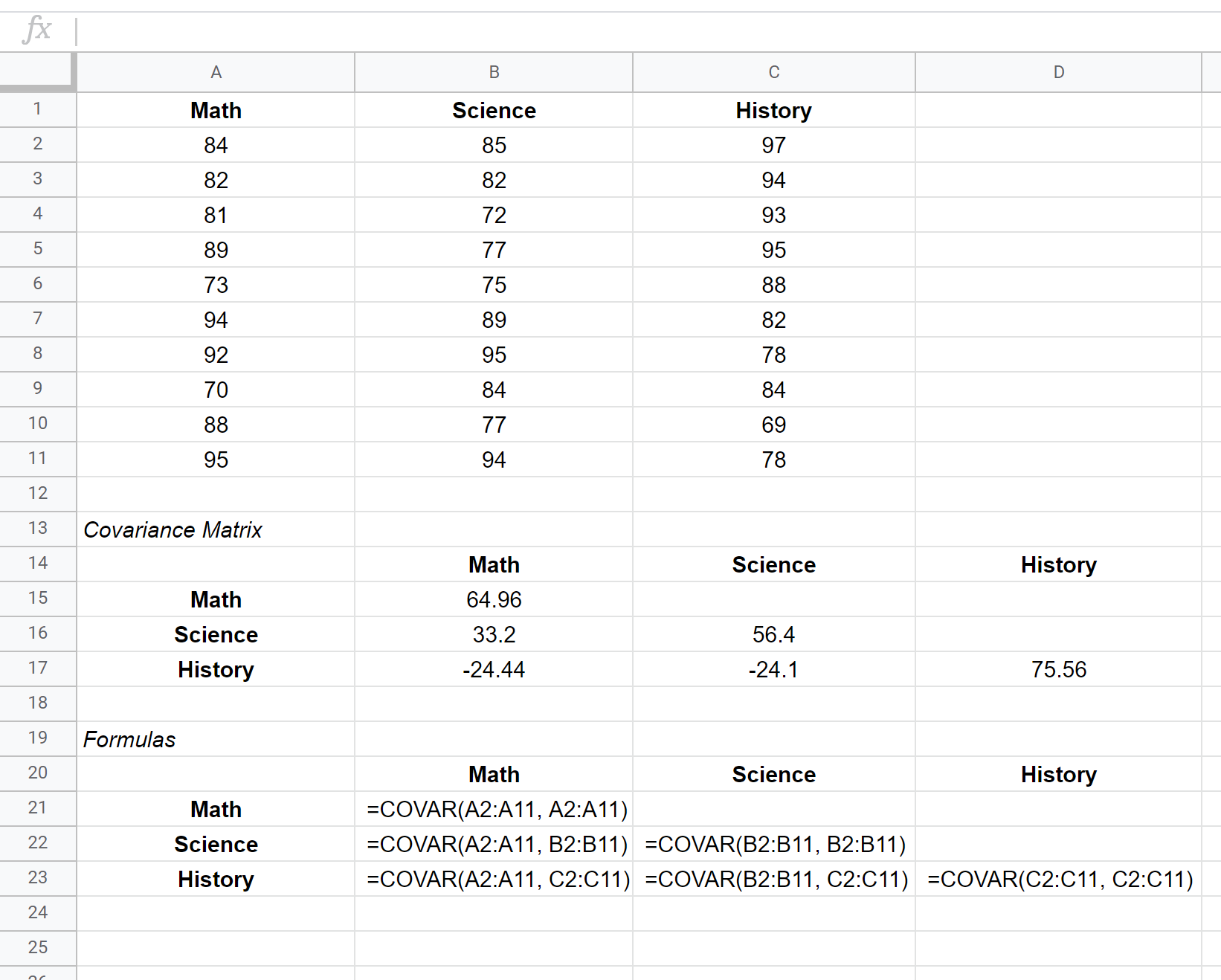
このデータセットの共分散行列はセルB15:D17に表示され、共分散行列の作成に使用される式は以下のセルB21:D23に表示されます。

共分散行列を解釈する方法

共分散行列を取得したら、行列値を解釈するのは簡単です。

マトリックスの対角に沿った値は、単に各被験者の分散です。例えば：

• 数学の得点の分散は 64.96 です
• 科学の得点の分散は 56.4 です
• 過去のスコア分散は 75.56 です

行列の他の値は、異なる被験者間の共分散を表します。例えば：

• 数学と科学のスコア間の共分散は 33.2 です。
• 数学と歴史のスコア間の共分散は -24.44 です。
• 科学スコアと歴史スコアの間の共分散は -24.1 です。

共分散の正の数は、 2 つの変数が並行して増加または減少する傾向があることを示します。たとえば、数学と科学には正の共分散 (33.2) があり、数学の得点が高い生徒は科学の得点も高い傾向があることを示しています。同様に、数学の成績が悪い生徒は、科学の成績も悪い傾向があります。

共分散の負の値は、 1 つの変数が増加すると、2 番目の変数が減少する傾向があることを示します。たとえば、数学と歴史には負の共分散 (-24.44) があり、数学の得点が高い生徒は歴史の得点が低い傾向があることを示しています。同様に、数学の得点が低い生徒は歴史の得点が高くなる傾向があります。

追加リソース

Excel で共分散行列を作成する方法
R で共分散行列を作成する方法
Python で共分散行列を作成する方法
SPSS で共分散行列を作成する方法