関節周波数: 定義と例
二元頻度表は、 2 つのカテゴリ変数の頻度を表示する表です。
たとえば、次の二元表は、100 人に野球、バスケットボール、サッカーのどのスポーツが好きかを尋ねたアンケートの結果を示しています。
行には回答者の性別が表示され、列には回答者が選択したスポーツが表示されます。
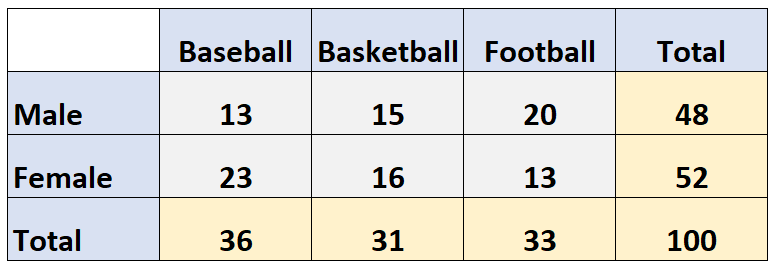
限界周波数は、表の余白に示されている周波数です。
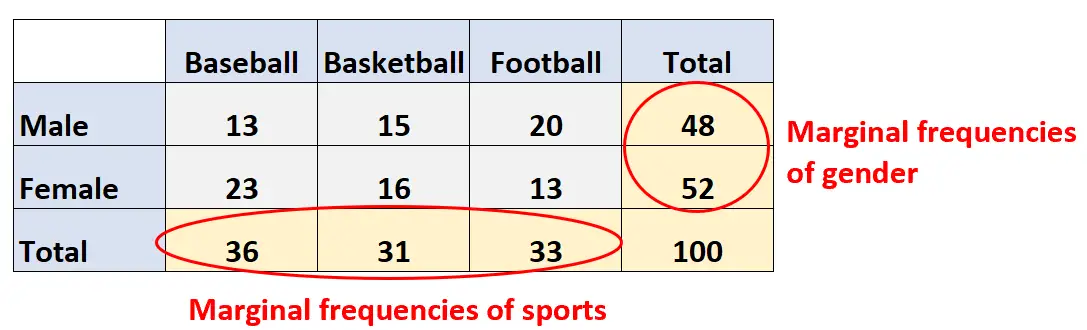
これらの値から、各変数の合計値がわかります。例えば:
- 合計36 人の回答者が好きなスポーツとして野球を選択しました
- 合計31 人の回答者が好きなスポーツとしてバスケットボールを選択しました
- 合計33 人の回答者が好きなスポーツとしてサッカーを選択しました
次のことも確認できます。
- 回答者は男性48名でした。
- 回答者は計52名が女性でした
ジョイント周波数は、表のセルに表示される周波数です。

これらの値は、同時に発生する 2 つの値の頻度を示すため、「結合」頻度と呼ばれます。
たとえば、次のことがわかります。
- 男性で野球が好きという回答者は計13人だった。
- バスケットボールを好む男性の回答者は合計15 人でした。
- 合計20 人の回答者が男性で、サッカーを好みました。
- 女性で野球が好きという回答者は計23人だった。
- バスケットボールを好む女性の回答者は合計16 人でした。
- 合計13 人の回答者が女性で、サッカーを好みました。
すべての結合頻度の合計が回答者の総数に相当することに注意してください。
調査回答者数の合計 = 13 + 15 + 20 + 23 + 16 + 13 = 100 。
関節相対周波数とは何ですか?
結合相対頻度は、別の変数に対する1 つの変数の頻度を示します。
たとえば、先ほどの複式エントリのテーブルを考えてみましょう。

質問 1:調査回答者が女性である場合、野球を好む共同相対頻度はどれくらいですか?
この質問に答えるために、女性の回答を含む行のみを考慮します。次に、野球を好む女性の数を女性の総数で割ります。
これは、23/52 = 0.4423 = 44.23%となります。

つまり、女性回答者全体の 44.23% が、好きなスポーツとして野球を好むことになります。
質問 2:好きなスポーツとしてサッカーを好むとすると、調査回答者が男性である共同相対度数はどれくらいですか?
この質問に答えるために、好きなスポーツとしてサッカーが含まれるセクションのみを考慮します。次に、サッカーを好む男性の数を取得し、それをサッカーを好む回答者の総数で割ります。
これは、20/33 = 0.606 = 60.6%となります。

つまり、サッカーを好む調査回答者全体の 60.6% が男性であるということです。