分布関数

によるベンジャミン・アンダーソン博士 8月 5, 2023 確率 0コメント

この記事では、分布関数の説明、その値の計算方法、および分布関数の実際の例を示します。さらに、分布関数と密度関数の違いも確認できるようになります。

分配関数とは何ですか?

分布関数は、累積分布関数とも呼ばれ、分布の累積確率を示す数学関数です。つまり、任意の値の分布関数のイメージは、変数がその値またはそれより低い値を取る確率に等しくなります。

累積分布関数は頭字語 FDA で呼ばれることもありますが、通常の記号は大文字の F です。

したがって、分布関数は次の式で定義されます。

$F(x)=P[X\leq x]$

分布関数の計算方法

次に、確率分布が離散的であるか連続的であるかに応じて分布関数の値を計算する方法を説明します。

秘密のボックス

確率変数が離散型の場合、累積分布関数はx以下のすべての値の確率の合計に等しくなります。

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

金

$f(u)$

は、離散変数に関連付けられた確率関数です。

継続案件

確率変数が連続の場合、累積分布関数は、マイナス無限大から問題の値までの密度関数の積分に相当します。

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

金

$f(u)$

は連続変数に関連付けられた密度関数です。

分布関数の例

分布関数の定義を理解したところで、分布関数の値を計算する方法を学ぶための実践的な例を段階的に見てみましょう。

コインを 4 回投げるランダム実験の分布関数を計算します。

この演習を解くには、まず 4 回のコイン投げで得られる表の数に関連するすべての確率を計算する必要があります。

したがって、これは離散変数であるため、分布関数のイメージを決定するには、問題の変数の値まで確率を加算するだけで十分です。

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

したがって、4 つの独立したコインを投げることによる表向きの分布関数の値は次のようになります。

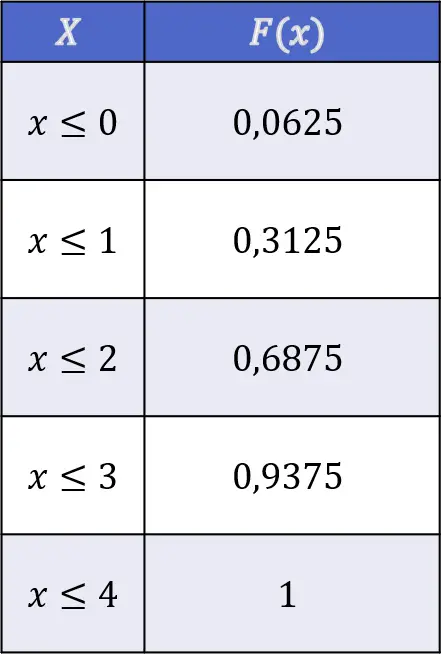
分布関数の性質

変数のタイプに関係なく、分布関数には常に次のプロパティがあります。

累積分布関数の値は 0 ～ 1 です。

$0\leq F(x) \leq 1$

x が無限大に近づく傾向があるときの分布関数の極限は 1 に等しくなります。

$\displaystyle\lim_{x\to +\infty} F(x)=1$

一方、 x がマイナス無限大に近づくときの分布関数の極限はゼロになります。

$\displaystyle\lim_{x\to -\infty} F(x)=0$

その特性により、分布関数は単調かつ非減少です。

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

さらに、
$a\leq b$

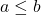
以下の式が成り立つ。

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

分布関数と密度関数

最後に、分布関数と密度関数の違いについて説明します。これら 2 つの統計概念は混同されることが多いためです。

分布関数と密度関数の違いは、それらが定義する確率のタイプです。密度関数は変数が特定の値を取る確率を表し、分布関数は変数の累積確率を表します。

つまり、分布関数は、変数が特定の値以下である確率を計算するために使用されます。

密度関数は連続変数のみを参照するため、この区別は調査対象の変数が連続変数である場合にのみ意味があることに注意してください。

平均 1、標準偏差 0.5 の正規分布に従う変数の密度関数と比較して、分布関数のグラフ表示がどのように変化するかに注目してください。

密度関数の詳細については、次の記事を参照してください。

➤参照:密度関数

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る