分散の仮説検定

によるベンジャミン・アンダーソン博士 8月 3, 2023 統計 0コメント

この記事では、分散の仮説検定とは何かについて説明します。したがって、分散仮説検定の公式と、さらに段階的に解決される演習が見つかります。

分散の仮説検定とは何ですか?

分散の仮説検定は、母集団分散の帰無仮説を棄却するかどうかを決定するために使用される統計手法です。言い換えれば、分散仮説検定は、母集団の分散の値に関する仮説を棄却または受け入れるために使用されます。

具体的には、分散に関する仮説検定統計量の値と選択した有意水準に応じて、帰無仮説が拒否されるか受け入れられます。

仮説検定にはさまざまな名前があり、仮説対比、仮説検定、有意性検定などと呼ばれることもあります。

分散の仮説検定公式

分散の仮説検定統計量は、サンプルサイズからサンプル分散の 1 倍を引いたものを母分散の提案された値で割ったものと等しくなります。分散の仮説検定統計量にはカイ二乗分布があります。

したがって、分散の仮説検定統計量を計算する式は次のようになります。

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

金：

$\chi^2$

は分散の仮説検定統計量であり、カイ二乗分布を持ちます。
$n$

はサンプルサイズです。
$s^2$

は標本分散です。
$\sigma^2$

は提案された母集団分散です。

統計の結果を解釈するには、得られた値をテストの臨界値と比較する必要があります。

分散の仮説検定が両側検定である場合、統計量が臨界値より大きい場合、帰無仮説は棄却されます。
$\chi_{1-\alpha/2|n-1}^2$

またはクリティカル値が以下の場合

$\chi_{\alpha/2|n-1}$

。
分散の仮説検定が右裾に一致する場合、統計量が臨界値より大きい場合、帰無仮説は棄却されます。
$\chi_{1-\alpha|n-1}^2$

。
分散の仮説検定が左裾に一致する場合、統計量が臨界値未満であれば帰無仮説は棄却されます。
$\chi_{\alpha|n-1}$

。

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

分散の重要仮説検定値は、カイ二乗分布表から取得されます。カイ二乗分布の自由度はサンプルサイズから 1 を引いたものであることに注意してください。

仮説分散検定の実世界の例

分散仮説検定の定義とその式が何であるかを理解した後、概念の理解を完了するために具体的な例を見ていきます。

工場には自動車の部品を高精度で生産する機械があります。しかし、現在は 8 mm ²を超えるギャップを持つ部品を製造していると考えられています。この仮説を否定するために、25 個のサンプルが分析され、そのサンプル分散は 9.1 mm ²でした。最初の仮説は有意水準 α=0.05 で棄却できますか?

この分散仮説検定の帰無仮説と対立仮説は次のとおりです。

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> 帰無仮説を棄却できるかどうかを判断するには、上記の式を使用して分散の仮説検定統計量を計算します。 <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

ここで、カイ二乗分布表の 24 自由度の右裾と有意水準 α=0.05 に対応する臨界値を探します。

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

したがって、計算された統計量は検定の臨界値より小さいため、分散仮説検定の帰無仮説は棄却されず、対立仮説が棄却されます。

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤参照:母平均の仮説検定
➤参照:人口比率の仮説検定

2 つの母集団の分散に対する仮説検定

2 母集団分散仮説検定は、 2 つの異なる母集団の分散が等しいという仮説を棄却または受け入れるために使用されます。

したがって、2 つの母集団の分散に関する仮説検定の帰無仮説は常に次のようになります。

$H_0: \sigma^2_1=\sigma^2_2$

対立仮説は、次の 3 つのオプションのいずれかになります。

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

この場合、2 つの母集団の分散に対する仮説検定統計量を計算する式は次のとおりです。

$F=\cfrac{s_1^2}{s_2^2}$

金：

$F$

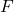
は、 F 分布に従う 2 つの母集団の分散の仮説検定統計量です。
$\sigma_1^2$

は母集団 1 の分散です。
$\sigma_2^2$

は母集団 2 の分散です。
$s_1^2$

はサンプル 1 の分散です。
$s_2^2$

はサンプル 2 の分散です。
$n_1$

サンプルサイズは1です。
$n_2$

サンプルサイズは2です。

Snedecor F 分布は対称ではないため、帰無仮説は次の基準に基づいて棄却されます。

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{黒} \ \text{もし }F \sigma_2^2 \ \color{オレンジ}\bm{\longrightarrow}\color{黒} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ 再確認 } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{オレンジ}\bm{\longrightarrow}\color{黒} \ \text{Si } F

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る