Anova と回帰: 違いは何ですか?
統計でよく使用される 2 つのモデルは、ANOVA モデルと回帰モデルです。
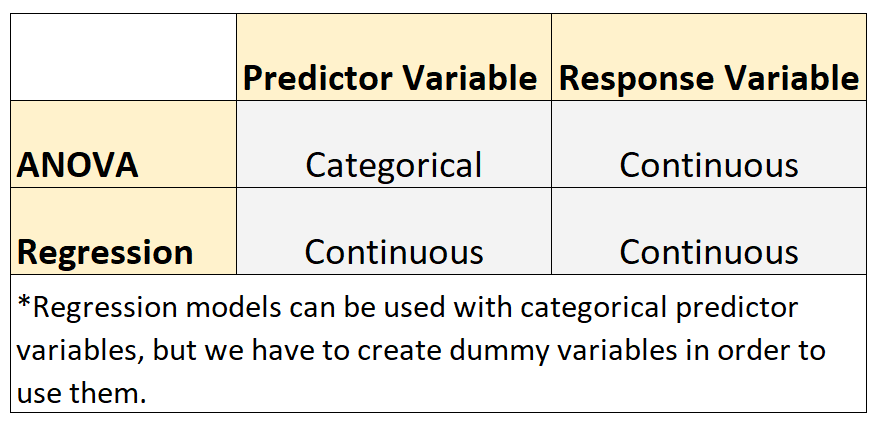
これら 2 種類のモデルには次の類似点があります。
- 各モデルの応答変数は連続的です。連続変数の例には、体重、身長、長さ、幅、時間、年齢などが含まれます。
ただし、これら 2 種類のモデルには次のような違いがあります。
- ANOVA モデルは、予測変数がカテゴリカルである場合に使用されます。カテゴリ変数の例には、教育レベル、目の色、婚姻状況などが含まれます。
- 回帰モデルは、予測変数が連続である場合に使用されます。*
*回帰モデルはカテゴリカル予測変数とともに使用できますが、使用するにはダミー変数を作成する必要があります。
次の例は、実際に ANOVA または回帰モデルをいつ使用するかを示しています。
例 1: 推奨される ANOVA モデル
生物学者が、4 つの異なる肥料が 1 か月間の植物の平均成長 (インチ単位) につながるかどうかを知りたいとします。これをテストするために、彼女は各肥料を 20 個の植物に適用し、1 か月後の各植物の成長を記録しました。
このシナリオでは、予測変数があり、それがカテゴリカルであるため、生物学者は一元配置分散分析モデルを使用して肥料間の差異を分析する必要があります。
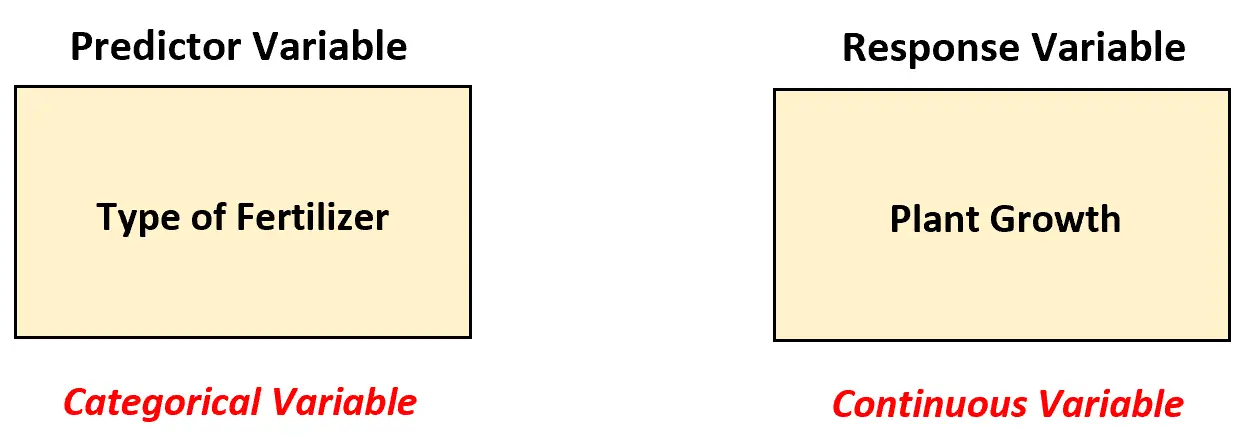
つまり、予測変数の値は次の「カテゴリ」に分類できます。
- 肥料1
- 肥料2
- 肥料3
- 肥料4
一元配置分散分析により、生物学者は植物の平均成長が 4 つの異なる肥料間で等しいかどうかがわかります。
例 2: 推奨される回帰モデル
不動産業者が面積と不動産価格の関係を理解したいとします。この関係を分析するために、彼は特定の都市の 200 戸の住宅の面積と価格に関するデータを収集しました。
このシナリオでは、予測変数 (平方フィート) が連続であるため、不動産業者は単純な線形回帰モデルを使用してこれら 2 つの変数間の関係を分析する必要があります。
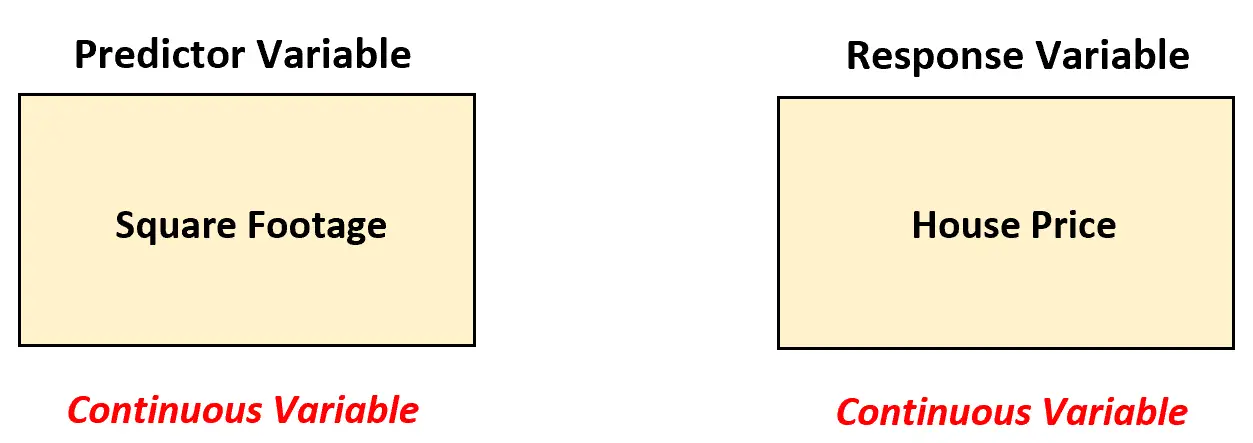
単純な線形回帰を使用すると、不動産業者は次の回帰モデルを当てはめることができます。
不動産価格 = β 0 + β 1 (平方面積)
β 1の値は、追加の平方フィートごとに関連する住宅価格の平均変化を表します。
これにより、不動産業者は面積と物件価格の関係を定量化できるようになります。
例 3: 優先ダミー変数を使用した回帰モデル
不動産業者が、予測変数「面積」および「住宅タイプ」(一戸建て、アパート、タウンハウス) と不動産価格の応答変数との関係を理解したいとします。
このシナリオでは、不動産業者は、「住宅タイプ」が現在カテゴリ変数であるため、ダミー変数に変換することで重線形回帰を使用できます。
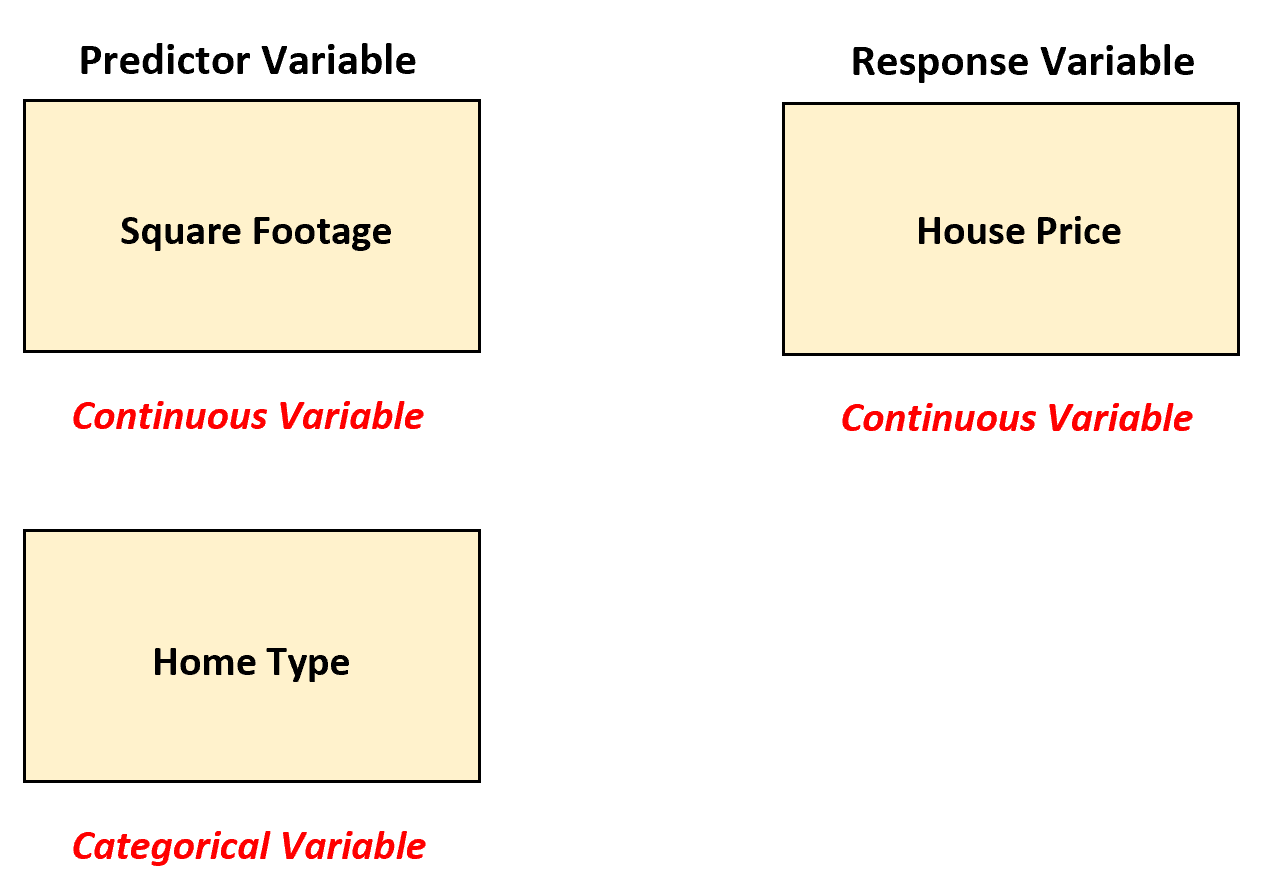
不動産業者は、次の重線形回帰モデルを当てはめることができます。
不動産価格 = β 0 + β 1 (面積) + β 2 (一戸建て) + β 3 (アパート)
モデル係数を解釈する方法は次のとおりです。
- β 1 : 1 平方フィート追加した場合の住宅価格の平均変化。
- β 2 :平方フィートが一定であると仮定した場合の、一戸建て住宅とタウンハウスの平均価格差。
- β 3 :表面積が一定であると仮定した場合の、一戸建てとアパートの平均価格差。
さまざまな統計ソフトウェアでダミー変数を作成する方法については、次のチュートリアルを参照してください。
追加リソース
次のチュートリアルでは、ANOVA モデルについて詳しく説明します。
次のチュートリアルでは、線形回帰モデルについて詳しく説明します。