Anova モデルの帰無仮説を理解する
一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
一元配置分散分析では、次の帰無仮説と対立仮説が使用されます。
- H 0 : μ 1 = μ 2 = μ 3 = … = μ k (すべてのグループ平均が等しい)
- H A :少なくとも 1 つのグループの平均が異なります 休む
帰無仮説を棄却すべきかどうかを決定するには、ANOVA 表の結果の p 値を参照する必要があります。
p 値が特定の有意水準 (0.05 など) を下回っている場合、帰無仮説を棄却し、すべてのグループ平均が等しいわけではないと結論付けることができます。
二元配置分散分析は、 2 つの変数 (「因子」と呼ばれることもあります) に割り当てられた 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
二元配置分散分析では、3 つの帰無仮説を同時に検定します。
- すべてのグループ平均は最初の変数の各水準で等しい
- すべてのグループ平均は 2 番目の変数の各水準で等しい
- 2 つの変数間に交互作用効果はありません
各帰無仮説を棄却すべきかどうかを決定するには、二元配置分散分析表の結果の p 値を参照する必要があります。
次の例は、一元配置分散分析と二元配置分散分析で帰無仮説を棄却するかどうかを決定する方法を示しています。
例 1: 一元配置分散分析
3 つの異なる試験準備プログラムが、特定の試験で異なる平均点につながるかどうかを知りたいとします。これをテストするために、研究に参加する 30 人の学生を募集し、3 つのグループに分けます。
各グループの学生は、次の 3 週間、3 つの試験準備プログラムのうち 1 つを使用して試験の準備をするようにランダムに割り当てられます。 3 週間の終わりに、生徒全員が同じ試験を受けます。
各グループの試験結果は以下のとおりです。

これらの値を 一元配置分散分析計算機に入力すると、出力として次の分散分析テーブルを受け取ります。

p 値が0.11385であることに注意してください。
この特定の例では、次の帰無仮説と対立仮説を使用します。
- H 0 : μ 1 = μ 2 = μ 3 (各グループの試験の平均点は等しい)
- H A :少なくとも 1 つのグループの平均が異なります 休む
ANOVA 表の p 値は 0.05 未満ではないため、帰無仮説を棄却できません。
これは、3 つのグループの平均試験得点の間に統計的に有意な差があると言える十分な証拠がないことを意味します。
例 2: 二元配置分散分析
植物学者が、日光への曝露や水やりの頻度が植物の成長に影響を与えるかどうかを知りたいとします。
彼女は 40 個の種を植え、日光への曝露や水やりの頻度などのさまざまな条件で 2 か月間成長させます。 2 か月後、彼女は各植物の高さを記録します。結果を以下に示します。

上の表では、各条件の組み合わせで 5 つの植物が栽培されたことがわかります。
たとえば、5 つの植物を毎日水やり、日光を当てずに育てたところ、2 か月後の高さは 4.8 インチ、4.4 インチ、3.2 インチ、3.9 インチ、4.4 インチでした。

Excel で二元配置分散分析を実行し、次の結果が得られます。
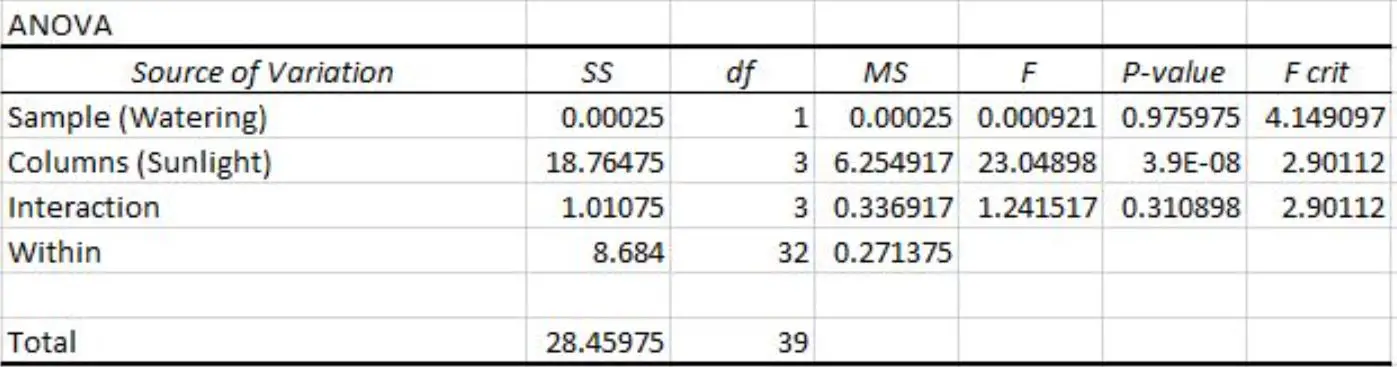
二元配置 ANOVA 表の結果では、次の p 値が確認できます。
- 水やり頻度の p 値は0.975975です。これは、有意水準 0.05 では統計的に有意ではありません。
- 太陽光への曝露の p 値は3.9E-8 (0.000000039)です。これは、有意水準 0.05 で統計的に有意です。
- 水やりの頻度と日光への曝露の間の相互作用の p 値は0.310898です。これは、有意水準 0.05 では統計的に有意ではありません。
これらの結果は、日光への曝露が草丈に統計的に有意な影響を与える唯一の要因であることを示しています。
また、相互作用効果がないため、日光曝露の影響は水やり頻度の各レベルで一貫しています。
簡単に言えば、植物に毎日水やりをするか毎週水をやるかは、日光への曝露が植物に与える影響には影響しません。
追加リソース
次のチュートリアルでは、ANOVA モデルに関する追加情報を提供します。
ANOVA での F 値と P 値の解釈方法
ANOVA で平方和を計算する方法
ANOVA における高い F 値は何を意味しますか?