先行変数とは何ですか? (説明と例)
統計学では、研究者は多くの場合、独立変数と従属変数の関係を理解したいと考えます。
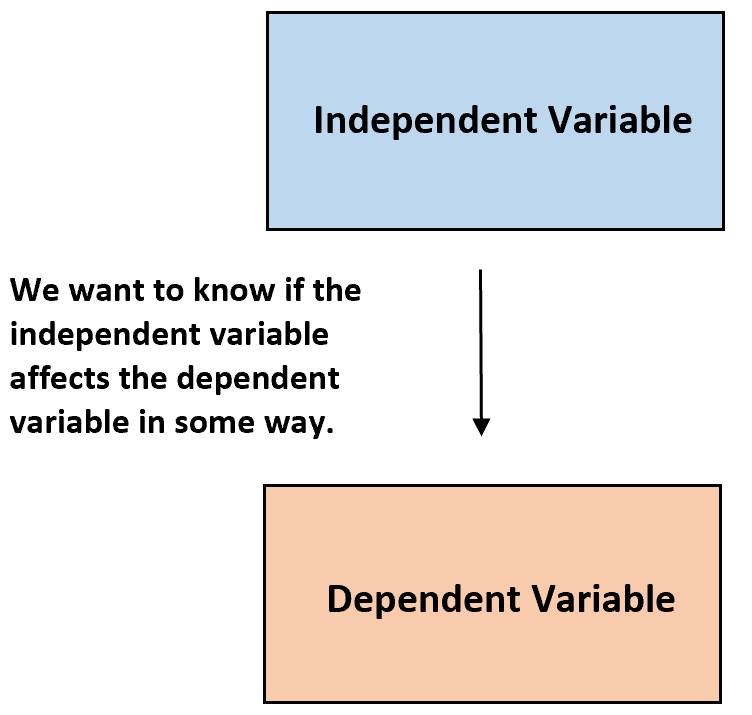
ただし、先行変数が存在する場合もあります。
先行変数は、調査対象の独立変数と従属変数の前に現れる変数であり、2 つの間の関係を説明するのに役立ちます。
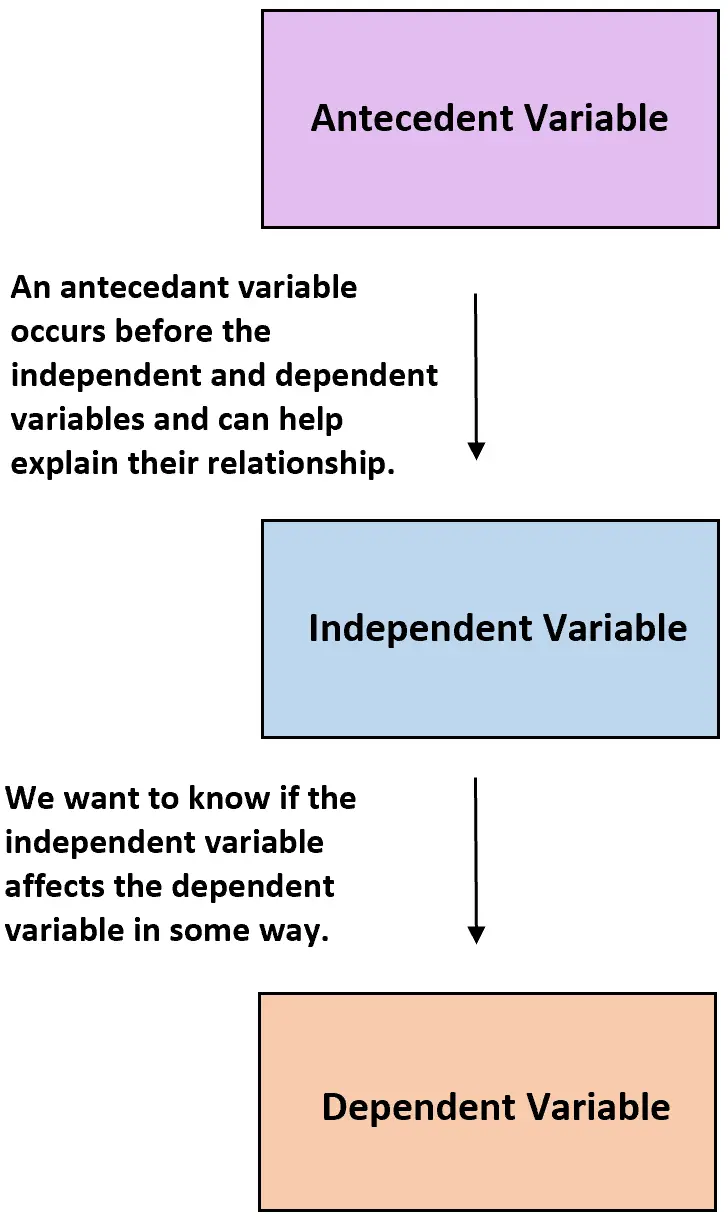
この定義は、 antecedent という単語が文字通り「以前または以前に存在する」という意味であることを覚えておくとわかります。
前の変数の例
先行変数はさまざまな研究シナリオに存在する可能性があります。ここではいくつかの例を示します。
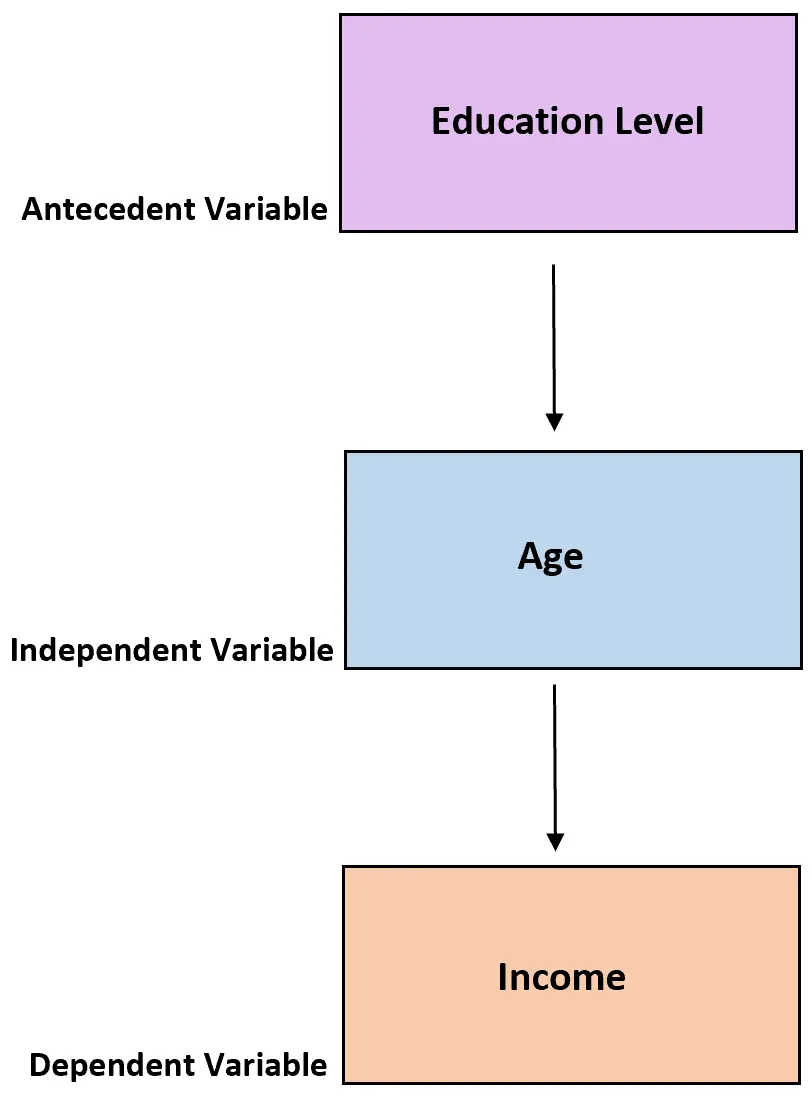
例1: 年齢と収入
研究者が年齢と年収の関係を研究したいとします。ただし、考慮すべき 2 つの変数間の関係を説明 (または部分的に説明) するのに役立つ可能性がある先行変数は、教育レベルです。これは年齢や収入と相関する傾向があるためです。
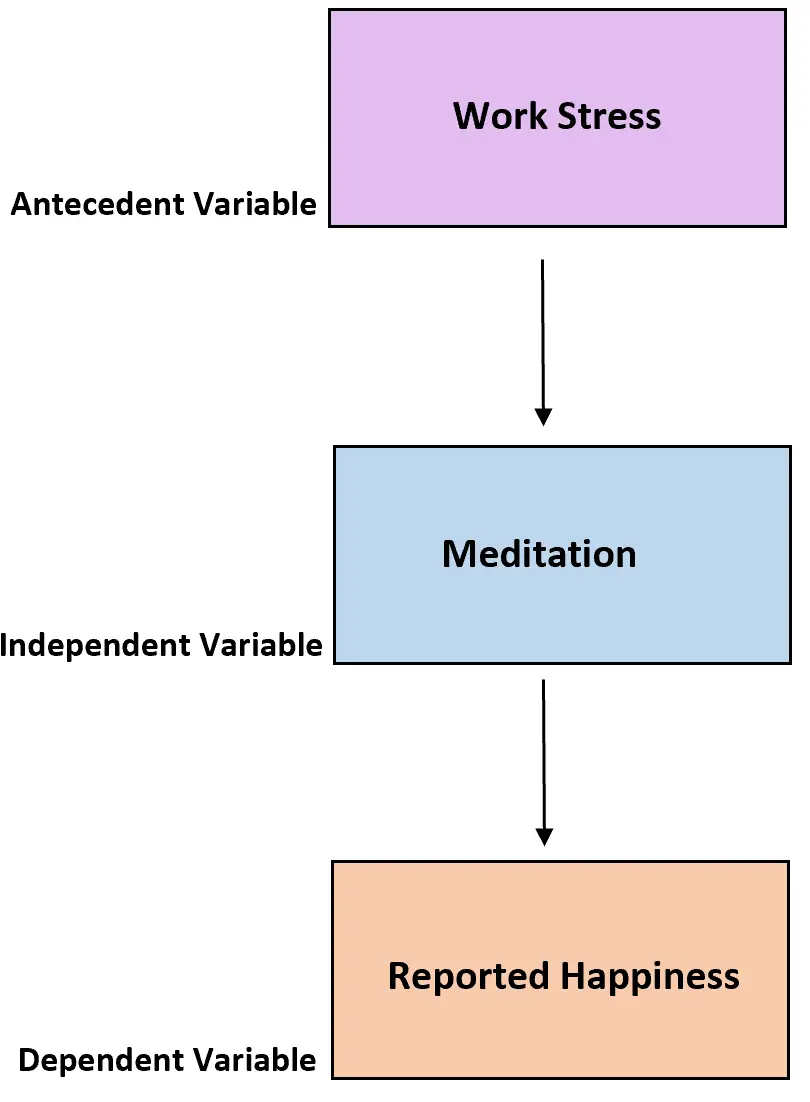
例 2: 瞑想と幸福
研究者が、瞑想と報告されている幸福度のレベルとの関係を研究したいと考えているとします。ただし、考慮すべき 2 つの変数間の関係を説明 (または部分的に説明) するのに役立つ可能性がある先行変数は、瞑想に利用できる自由時間と宣言された幸福の両方に影響を与える可能性があるため、仕事のストレスです。
以前の変数を制御する方法
実験では、研究者は先行変数を阻害要因として使用することで、先行変数を制御できる可能性があります。たとえば、教育レベルに基づいて参加者を「ブロック」に分け、ブロックごとに年齢と収入の関係を調査することができます。
回帰分析では、研究者は回帰モデルに先行変数を含めて、その効果を制御できます。たとえば、研究者は、教育レベルを一定に保ちながら、年齢の回帰係数を収入の平均変化として解釈できるように、教育レベルを回帰モデルの変数として含めることができます。
これらの両方のシナリオでは、これらの先行変数のデータがすぐに利用できると想定されていますが、常にそうであるとは限りません。たとえば、「仕事のストレス」が瞑想能力や幸福感に影響を与える可能性がある先行変数である可能性があることはわかっていても、数値化するのは難しいかもしれません。
関連する変数
先行変数に似ていて、独立変数と従属変数の間の関係にも影響を与える可能性がある 2 つの変数は次のとおりです。
1.無関係な変数: 研究では関心のない変数ですが、独立変数と従属変数の両方に影響を与える可能性があります。
2.中間変数: 独立変数と従属変数の間を結び付け、2 つの間の関係に直接影響を与える変数。
実験や研究を行うときは、これらのタイプの変数のそれぞれに注意してください。