割合の仮説検定
この記事では、統計学における仮説検定の割合について説明します。したがって、割合の仮説検定の公式と、その方法を完全に理解するための段階的な演習が見つかります。
割合の仮説検定とは何ですか?
比率仮説検定は、母集団比率の帰無仮説を棄却するかどうかを決定するために使用される統計手法です。
したがって、割合と有意水準の仮説検定統計量の値に応じて、帰無仮説は棄却されるか受け入れられます。
仮説検定は、仮説対比、仮説検定、または有意性検定とも呼ばれることがあることに注意してください。
割合の仮説検定公式
割合の仮説検定統計量は、サンプル割合の差から割合の提案値を引いたものを割合の標準偏差で割ったものに等しくなります。
したがって、比率の検定仮説の式は次のようになります。

金:
-

は、割合の仮説検定統計量です。
-

はサンプルの割合です。
-

提案された比率の値です。
-

はサンプルサイズです。
-

は比率の標準偏差です。
比率の仮説検定統計量を計算するだけでは十分ではなく、結果を解釈する必要があることに注意してください。
- 比率の仮説検定が両側である場合、統計量の絶対値が臨界値 Z α/2より大きい場合、帰無仮説は棄却されます。
- 比率の仮説検定が右裾に一致する場合、統計量が臨界値 Z αより大きい場合、帰無仮説は棄却されます。
- 割合の仮説検定が左裾に一致する場合、統計量が臨界値 -Z αより小さい場合、帰無仮説は棄却されます。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
臨界値は正規分布表から簡単に取得できることを覚えておいてください。
割合の仮説検定の例
比率の仮説検定の定義とその式が何であるかを理解したら、概念をよりよく理解するために例を解いていきます。
- メーカーによれば、特定の病気に対する薬の有効率は 70% です。研究者は割合が異なると信じているため、研究室ではこの薬の有効性をテストします。このため、この薬は1,000人の患者のサンプルで試験され、641人が治癒した。研究者の仮説を棄却するかどうかを決定するために、有意水準 5% で母集団の割合に対して仮説検定を実行します。
この場合、母集団の割合に対する仮説検定の帰無仮説と対立仮説は次のとおりです。
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
サンプルに含まれるこの薬によって治癒した人の割合は次のとおりです。
![]()
上記の式を適用して、割合の仮説検定統計量を計算します。
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
一方、有意水準は 0.05 であり、これは両側仮説検定であるため、検定の臨界値は 1.96 です。
![]()
結論として、検定統計量の絶対値は臨界値より大きいため、帰無仮説を棄却し、対立仮説を受け入れます。
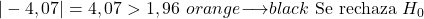 ➤参照:平均値の仮説検定
➤参照:平均値の仮説検定
2 つのサンプル比率に対する仮説検定
2 つのサンプルの比率に関する仮説検定は、 2 つの異なる母集団の比率が等しいという帰無仮説を棄却または受け入れるために使用されます。
したがって、2 サンプルの比率に対する仮説検定の帰無仮説は常に次のようになります。
![]()
一方、対立仮説は次の 3 つのオプションのいずれかになります。
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
2 つのサンプル比率に対する仮説検定統計量を計算する式は次のとおりです。
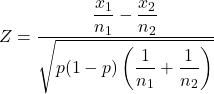
金:
-

は、2 つの標本比率の仮説検定統計量です。
-
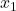
はサンプル 1 の結果の数です。
-
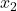
はサンプル 2 の結果の数です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
-

は 2 つのサンプルを合わせた比率です。
k 個のサンプル比率に対する仮説検定
k 個のサンプルの割合に関する仮説検定の目的は、異なる母集団の割合がすべて等しいかどうか、あるいは逆に異なる割合があるかどうかを判断することです。したがって、この場合の帰無仮説と対立仮説は次のようになります。
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
この場合、すべてのサンプルの合計比率は次のように計算されます。
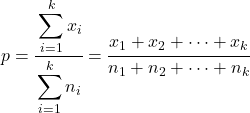
k 個のサンプル比率に対する仮説検定統計量を求める式は次のとおりです。
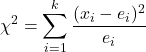
![]()
金:
-

は、k 個のサンプル比率に対する仮説検定統計量です。この場合、統計はカイ二乗分布に従います。
-

サンプル i の結果の数です。
-

はサンプルサイズ i です。
-

すべてのサンプルの合計の割合です。
-

はサンプル i から予想されるヒット数です。組み合わせた比率を乗じて計算されます

サンプルサイズによる

。