効果量: それが何か、そしてなぜそれが重要なのか
「統計的な有意性は、結果の中で最も興味をそそらないものです。結果を大きさの尺度で説明する必要があります。治療が人々に影響を与えるだけでなく、それが人々にどの程度影響を与えるかということです。 -ジーン・V・グラス
統計では、2 つのグループ間に統計的に有意な差があるかどうかを判断するためにp 値がよく使用されます。
たとえば、2 つの異なる勉強法が異なるテストのスコアにつながるかどうかを知りたいとします。したがって、20 人の生徒のグループが、ある勉強法を使用してテストの準備をしている一方で、別の 20 人の生徒のグループが別の勉強法を使用しています。次に、各生徒に同じテストを行います。
2 サンプルの t 検定を実行して平均の差を決定した後、検定の p 値は 0.001 であることがわかります。有意水準 0.05 を使用すると、2 つのグループの平均結果の間に統計的に有意な差があることを意味します。つまり、勉強のテクニックがテストの結果に影響を与えるのです。
ただし、p 値は、学習テクニックがテストのスコアに影響を与えることを示しますが、その影響の大きさは示しません。これを理解するには、効果量を知る必要があります。
効果量とは何ですか?
効果量は、2 つのグループ間の差異を定量化する方法です。
p 値は 2 つのグループ間に統計的に有意な差があるかどうかを知ることができますが、効果の大きさはその差が実際にどれくらい大きいかを知ることができます。実際には、p 値よりも効果量の方がはるかに興味深く、知っておくと役立ちます。
実行する分析の種類に応じて、効果の大きさを測定するには 3 つの方法があります。
1. 標準化された平均差
2 つのグループ間の平均差を調べたい場合、効果量を計算する適切な方法は、標準化された平均差を使用することです。使用する最も一般的な公式はコーエンのdとして知られており、次のように計算されます。
コーエンのD = ( x1 – x2 )/ s
ここで、 x 1とx 2はそれぞれグループ 1 とグループ 2 の標本平均であり、 sは 2 つのグループが抽出された母集団の標準偏差です。
この式を使用すると、効果の大きさを簡単に解釈できます。
- dが 1 の場合は、2 つのグループの平均が標準偏差 1 つだけ異なることを示します。
- dが 2 は、グループ平均が 2 標準偏差だけ異なることを意味します。
- dが 2.5 の場合は、2 つの平均が 2.5 標準偏差だけ異なることを示します。
効果量を解釈する別の方法は次のとおりです。効果量 0.3 は、グループ2の平均的な人のスコアがグループ1の人の平均より 0.3 標準偏差高く、したがってグループ1のスコアの 62% を超えていることを意味します。 。
次の表は、さまざまな効果の大きさと、それに対応するパーセンタイルを示しています。
| 効果の大きさ | グループ1の人々の平均を下回るグループ2の割合 |
|---|---|
| 0.0 | 50% |
| 0.2 | 58% |
| 0.4 | 66% |
| 0.6 | 73% |
| 0.8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99.9% |
効果サイズが大きいほど、各グループの平均的な個人間の差が大きくなります。
一般に、0.2 以下のd は小さな効果サイズとみなされ、約 0.5 のdは中程度の効果サイズとみなされ、0.8 以上のdは大きな効果サイズとみなされます。
したがって、2 つのグループの平均値に少なくとも 0.2 標準偏差の差がない場合、たとえ p 値が統計的に有意であっても、その差は重要ではありません。
2. 相関係数
2 つの変数間の定量的な関係を調べたい場合、効果量を計算する最も一般的な方法は、 ピアソン相関係数を使用することです。これは、2 つの変数XとYの間の線形関連性の尺度です。値は -1 から 1 までです。ここで、次のとおりです。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
ピアソン相関係数の計算式は非常に複雑ですが、興味がある方はここで確認できます。
相関係数がゼロから離れるほど、2 つの変数間の線形関係が強くなります。これは、変数XとYの値の単純な散布図を作成することによっても確認できます。
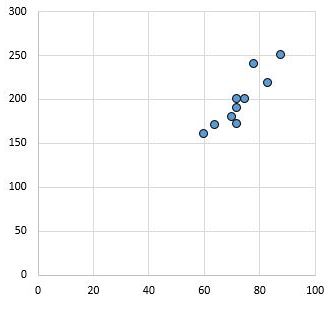
たとえば、次の散布図は、相関係数r = 0.94 の 2 つの変数の値を示しています。
この値はゼロからは程遠く、2 つの変数間に強い正の関係があることを示しています。
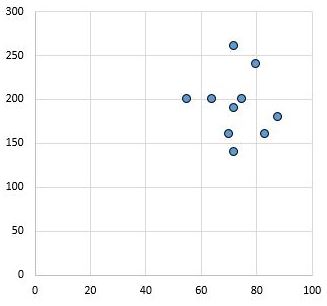
逆に、次の散布図は、相関係数r = 0.03 を持つ 2 つの変数の値を示しています。この値はゼロに近く、2 つの変数間に実質的に関係がないことを示しています。
一般に、ピアソン相関係数rの値が約 0.1 の場合は効果量が小さく、 rが約 0.3 の場合は効果量が中程度、 rが 0.5 以上の場合は効果量が大きいと考えられます。
3. オッズ比
治療グループの成功のオッズと対照グループの成功のオッズを研究したい場合、効果の大きさを計算する最も一般的な方法は、オッズ比を使用することです。
たとえば、次のテーブルがあるとします。
| 効果の大きさ | #成功 | #チェス |
|---|---|---|
| 治療群 | もっている | B |
| 対照群 | VS | D |
オッズ比は次のように計算されます。
オッズ比 = (AD) / (BC)
オッズ比が 1 から離れるほど、治療が実際の効果を生み出す可能性が高くなります。
P 値ではなく効果量を使用する利点
効果量には、p 値に比べていくつかの利点があります。
1.効果量は、2 つのグループ間の差がどれほど大きいか、または 2 つのグループ間の関連性がどの程度強いかをよりよく理解するのに役立ちます。 p 値は、有意差または有意な関連があるかどうかのみを示します。
2. p 値とは異なり、エフェクト サイズを使用すると、異なる設定で実施された異なる研究の結果を定量的に比較できます。このため、エフェクト サイズはメタ分析でよく使用されます。
3. P 値はサンプルサイズが大きいと影響を受ける可能性があります。サンプルサイズが大きいほど、仮説検定の統計的検出力が大きくなり、小さな効果も検出できるようになります。これにより、実際には意味がない可能性のある小さな効果量にもかかわらず、低い p 値が発生する可能性があります。
簡単な例でこれを明確に説明できます。2 つの勉強法が異なるテストのスコアにつながるかどうかを知りたいとします。ある学習手法を使用する 20 人の生徒のグループと、別の学習手法を使用する 20 人の生徒のグループがあります。次に、各生徒に同じテストを行います。
グループ 1 の平均スコアは90.65で、グループ 2 の平均スコアは90.75です。サンプル 1 の標準偏差は2.77で、サンプル 2 の標準偏差は2.78です。
独立した 2 サンプルの t 検定を実行すると、検定統計量は-0.113で、対応する p 値は0.91であることがわかります。テストの平均点間の差は統計的に有意ではありません。
ただし、2 つのサンプルのサンプル サイズが両方とも200であるにもかかわらず、平均と標準偏差がまったく同じままである場合を考えてみましょう。
この場合、独立した 2 サンプルの t 検定により、検定統計量が-1.97で、対応する p 値が0.05をわずかに下回ることが明らかになります。テストの平均点間の差は統計的に有意です。
サンプルサイズが大きいと統計的に有意な結論が得られる根本的な理由は、 t検定統計量の計算に使用される式にあります。
検定統計量t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
n 1と n 2が小さい場合、 t検定統計量の整数分母が小さいことに注意してください。そして、小さな数で割ると大きな数が得られます。これは、 t検定統計量が大きく、対応する p 値が小さくなり、統計的に有意な結果が得られることを意味します。
適切な効果量とはどれくらいだと考えられますか?
学生がよく尋ねる質問は、「適切な効果量とはどれくらいだと考えられますか?」というものです。
簡単に言うと、効果量は 2 つのグループ間の差異の大きさ、または 2 つのグループ間の関連の強さを測定するだけであるため、「良い」または「悪い」ということはできません。
ただし、次の経験則を使用して、効果の大きさが小さい、中程度、または大きいかを定量化できます。
コーエンのD:
- 0.2 以下のdは、効果量が小さいと考えられます。
- 0.5 のd は中程度の効果サイズとみなされます。
- 0.8 以上のd は、大きな効果量とみなされます。
ピアソン相関係数
- rの絶対値が 0.1 付近であれば、効果量は小さいと考えられます。
- 0.3 付近のrの絶対値は、中程度の効果量とみなされます。
- rの絶対値が 0.5 より大きい場合、効果量が大きいと見なされます。
ただし、「強い」相関の定義は分野によって異なる場合があります。さまざまな業界間で何が強い相関関係と考えられているかをよりよく理解するには、この記事を参照してください。