Leave-one-out 相互検証 (loocv) の概要
データセットに対するモデルのパフォーマンスを評価するには、モデルによって行われた予測が観察されたデータとどの程度一致するかを測定する必要があります。
これを測定する最も一般的な方法は、次のように計算される平均二乗誤差 (MSE) を使用することです。
MSE = (1/n)*Σ(y i – f(x i )) 2
金:
- n:観測値の総数
- y i : i 番目の観測値の応答値
- f( xi ): i番目の観測値の予測応答値
モデルの予測が観測値に近づくほど、MSE は低くなります。
実際には、次のプロセスを使用して特定のモデルの MSE を計算します。
1.データセットをトレーニング セットとテスト セットに分割します。
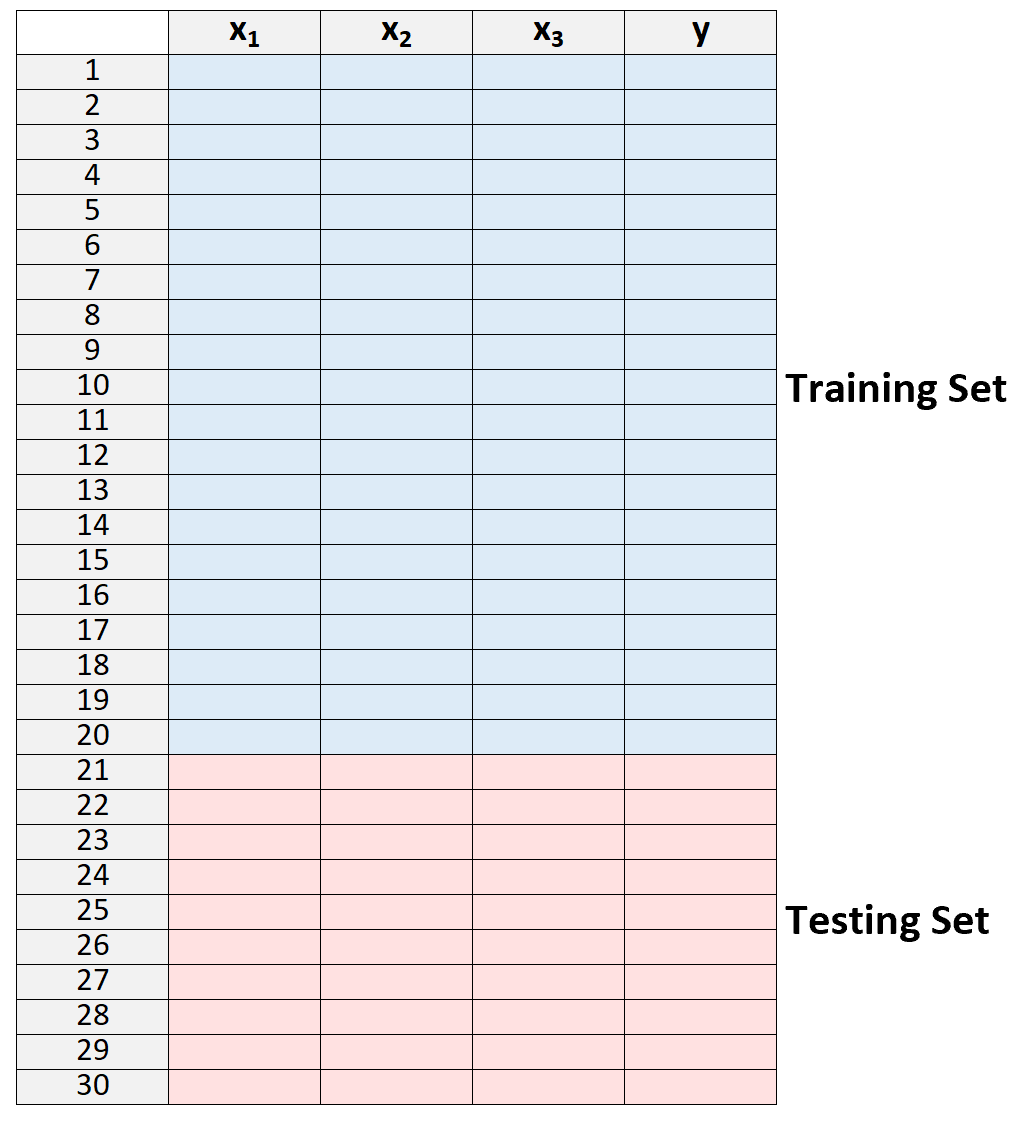
2.トレーニング セットのデータのみを使用してモデルを作成します。
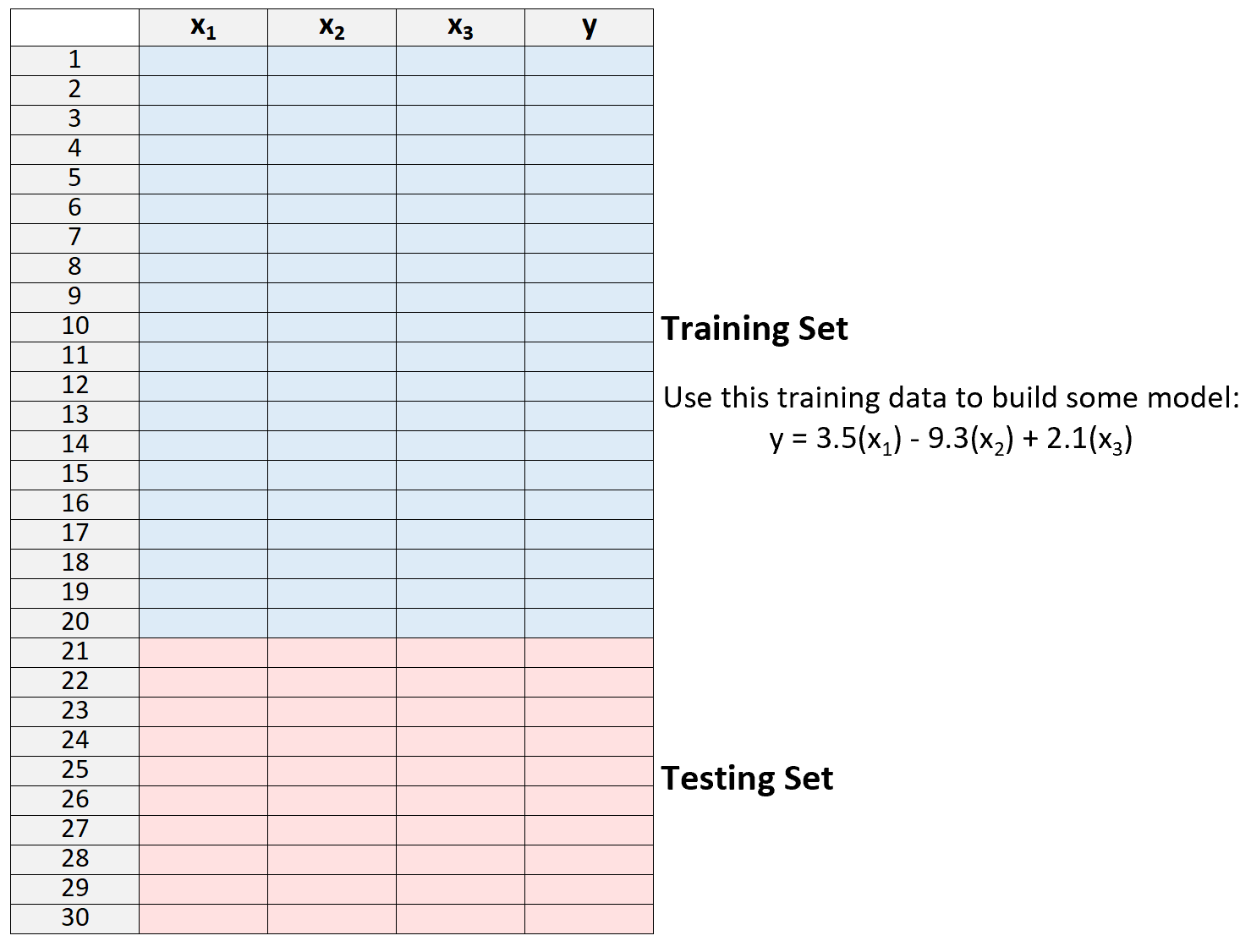
3.モデルを使用してテスト セットに関する予測を行い、MSE を測定します。これはテスト MSEと呼ばれます。 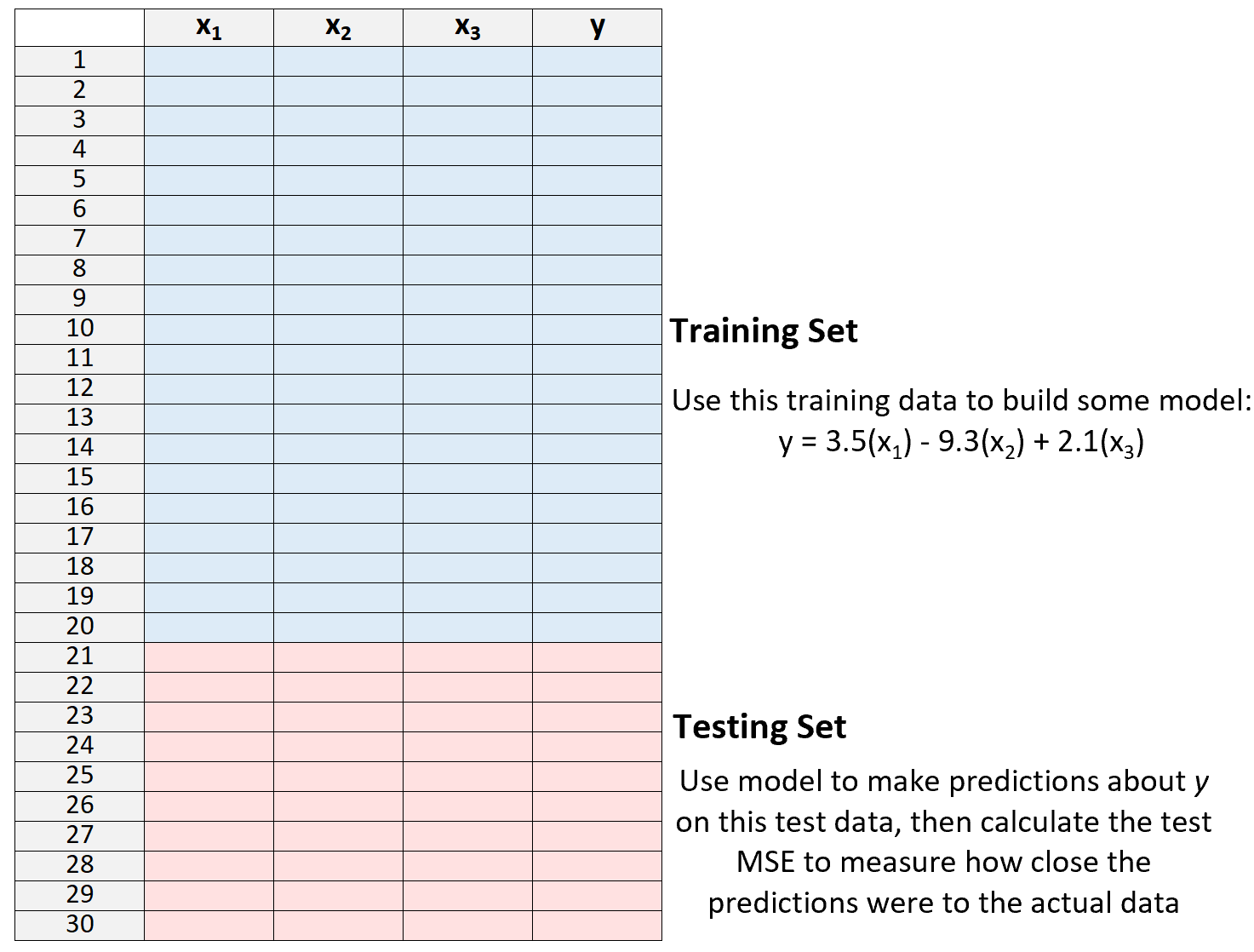
MSE テストでは、これまでに見たことのないデータ、つまりモデルの「トレーニング」に使用されていないデータに対してモデルがどの程度うまく機能するかを知ることができます。
ただし、単一のテスト セットを使用する場合の欠点は、MSE テストがトレーニング セットとテスト セットで使用される観測値に応じて大きく異なる可能性があることです。
トレーニング セットとテスト セットに異なる観測セットを使用すると、テスト MSE が大幅に大きくなったり、小さくなったりする可能性があります。
この問題を回避する 1 つの方法は、毎回異なるトレーニング セットとテスト セットを使用してモデルを複数回適合させ、すべてのテスト MSE の平均としてテスト MSE を計算することです。
この一般的な方法は相互検証として知られており、その特定の形式はLeave-One-Out 相互検証として知られています。
リーブワンアウト相互検証
Leave-one-out 相互検証では、次のアプローチを使用してモデルを評価します。
1.データセットをトレーニング セットとテスト セットに分割し、1 つを除くすべての観測値をトレーニング セットの一部として使用します。
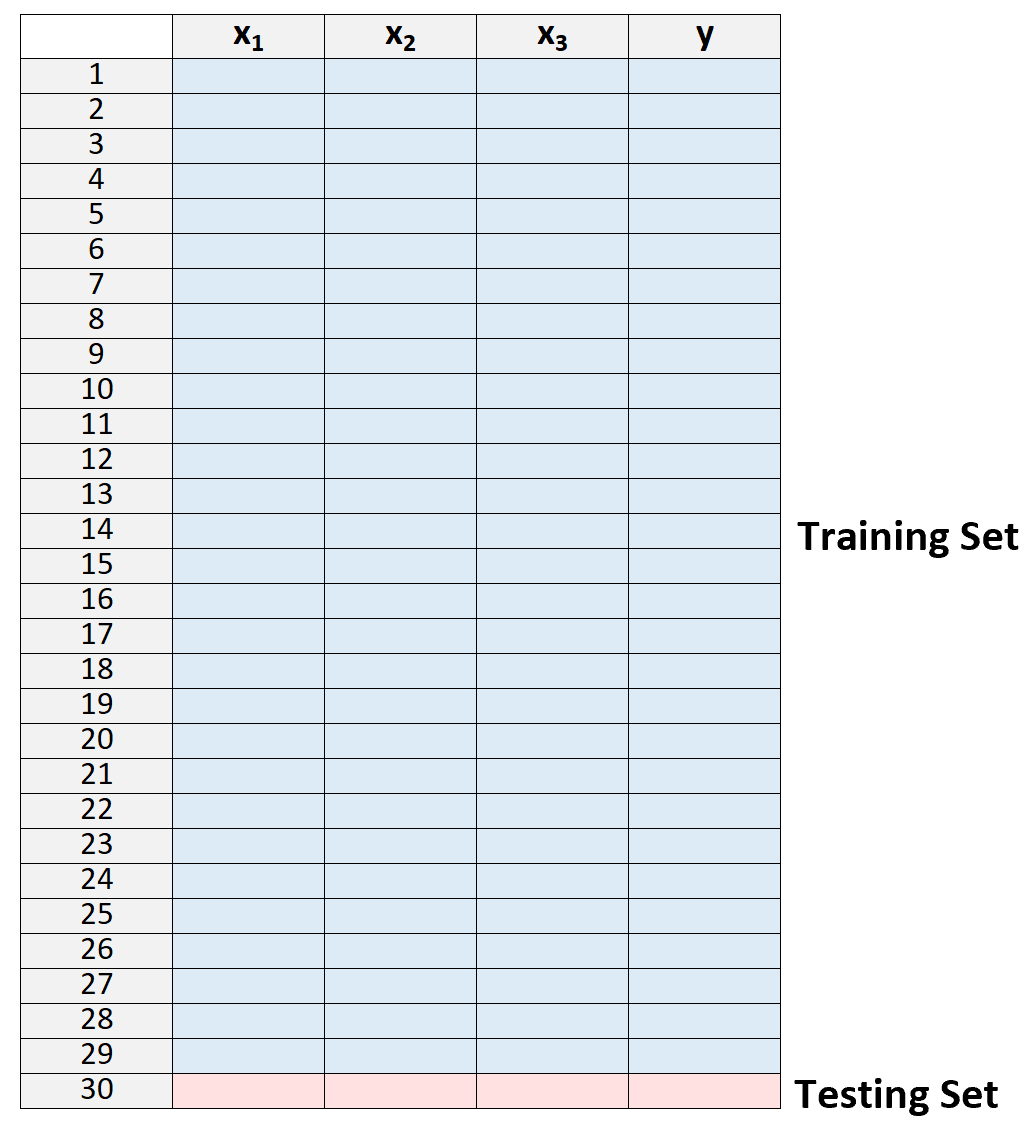
トレーニング セットの「外側」に 1 つの観測値だけを残すことに注意してください。これが、このメソッドの名前「leave-one-out」相互検証の由来です。
2.トレーニング セットのデータのみを使用してモデルを作成します。
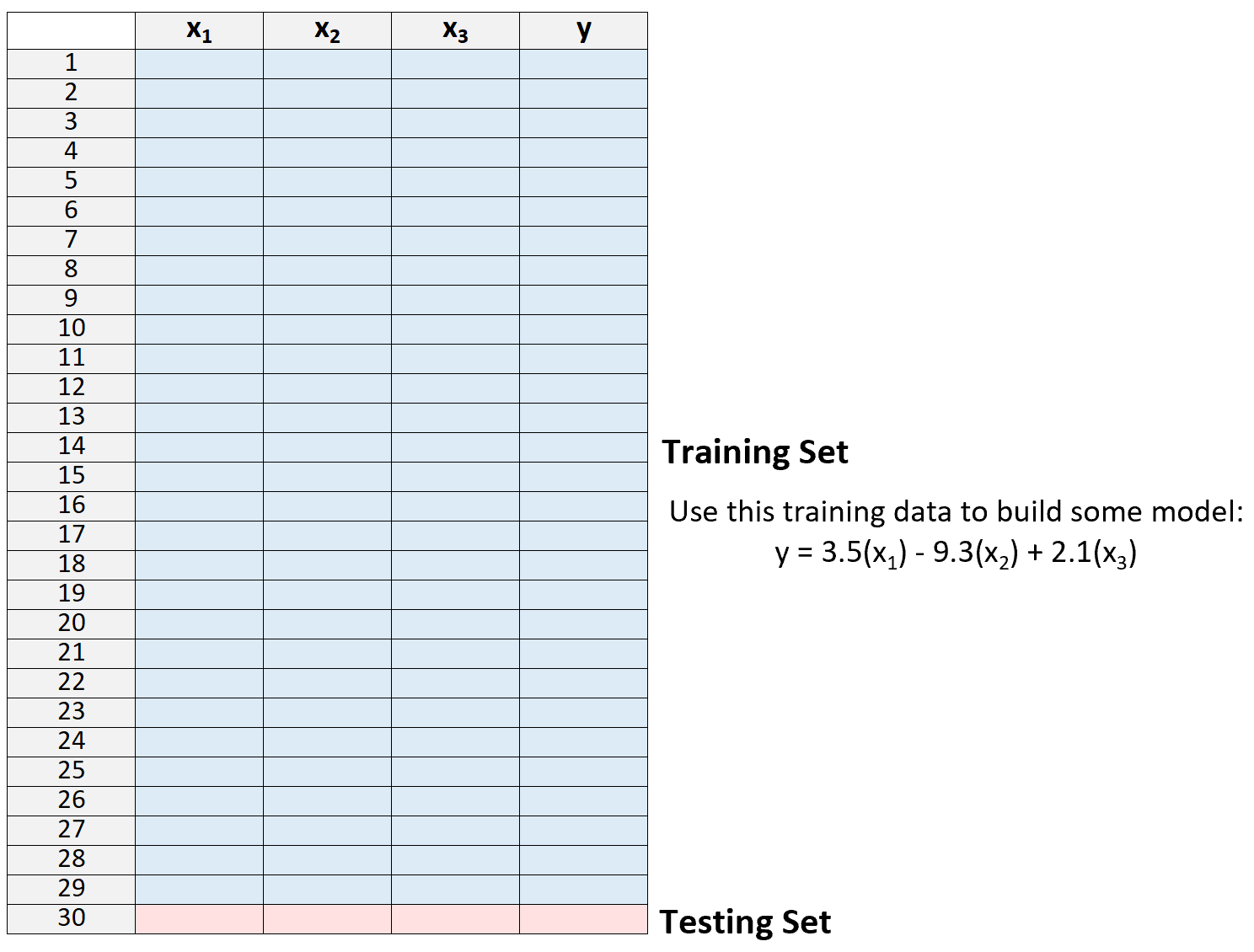
3.モデルを使用して、モデルから除外された単一の観測値の応答値を予測し、MSE を計算します。
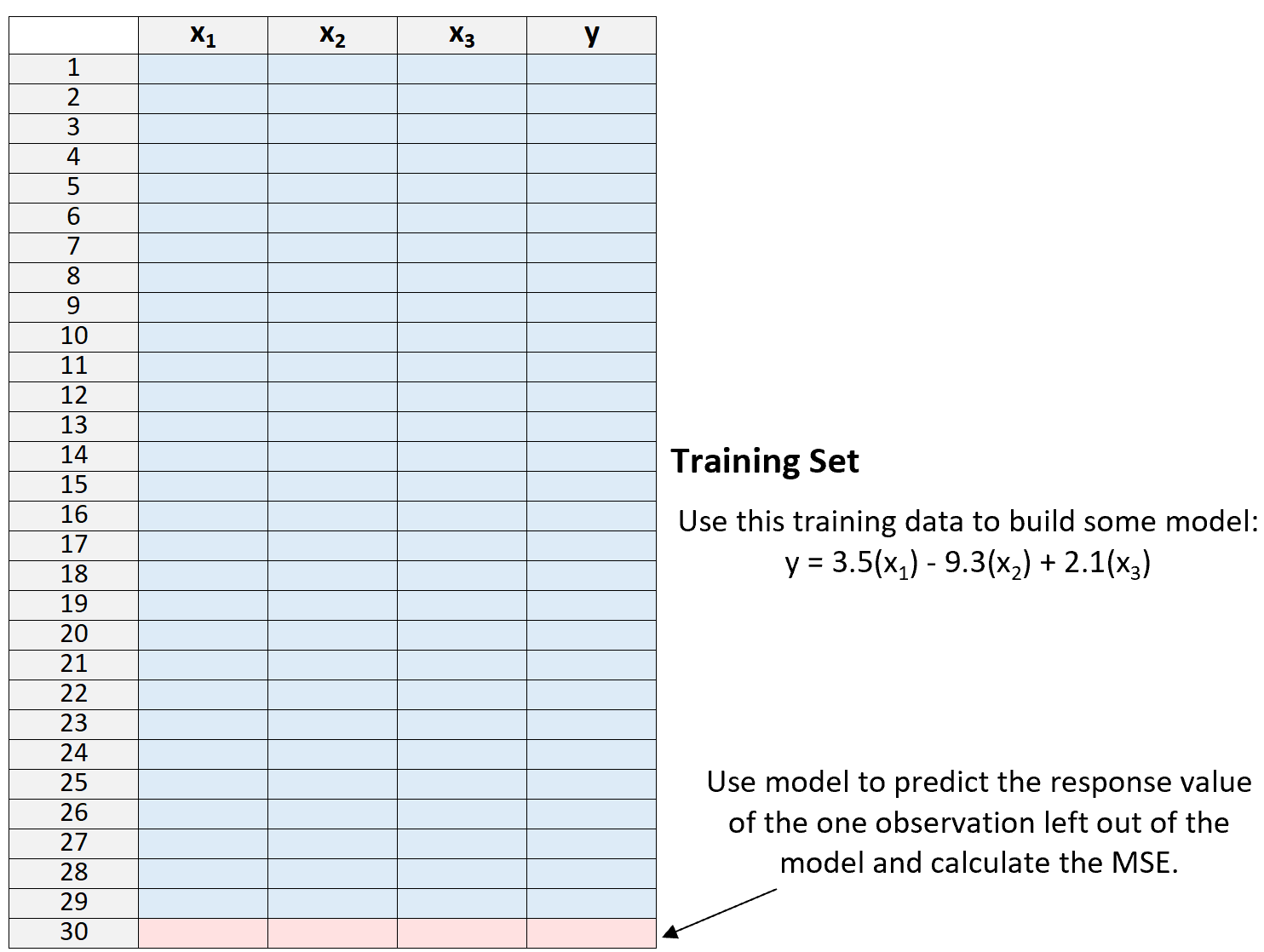
4.このプロセスをn回繰り返します。
最後に、このプロセスをn回繰り返します ( nはデータセット内の観測値の合計数です)。毎回トレーニング セットから異なる観測値を除外します。
次に、テスト MSE をすべてのテスト MSE の平均として計算します。
MSE テスト = (1/n)*ΣMSE i
金:
- n:データセット内の観測値の総数
- MSEi: i 番目のモデル フィッティング期間中の MSE テスト。
LOOCVのメリットとデメリット
Leave-one-out 相互検証には次の利点があります。
- n-1 個の観測値を含むデータセットにモデルを繰り返し適合させるため、単一のテスト セットを使用する場合と比較して、はるかに偏りの少ない MSE テストの測定値が得られます。
- 単一のテスト セットを使用する場合と比較して、テストの MSE が過大評価されない傾向があります。
ただし、ハンズオフ相互検証には次のような欠点があります。
- nが大きい場合、このプロセスを使用すると時間がかかることがあります。
- モデルが特に複雑で、データセットの適合に長い時間がかかる場合も、時間がかかる可能性があります。
- これは計算コストが高くなる可能性があります。
幸いなことに、現代のコンピューティングはほとんどの分野で非常に効率的になったため、LOOCV は何年も前よりもはるかに合理的な方法で使用できるようになりました。
LOOCV は回帰および分類のコンテキストでも使用できることに注意してください。回帰問題の場合は、MSE テストを予測と観測値の間の二乗平均平方根差として計算します。一方、分類問題の場合は、モデルのn回の繰り返し調整にわたって正しく分類された観測値のパーセンテージとして MSE テストを計算します。
R と Python で LOOCV を実行する方法
次のチュートリアルでは、R および Python で特定のモデルに対して LOOCV を実行する方法について段階的な例を示します。