単変量解析とは何ですか? (定義&例)
一変量分析という用語は、1 つの変数の分析を指します。接頭辞「uni」は「1」を意味するので、これを覚えておくとよいでしょう。
単変量解析の目標は、単一の変数の値の分布を理解することです。このタイプの分析を次の分析と比較できます。
- 二変量分析: 2 つの変数の分析。
- 多変量分析: 2 つ以上の変数の分析。
たとえば、次のデータセットがあるとします。
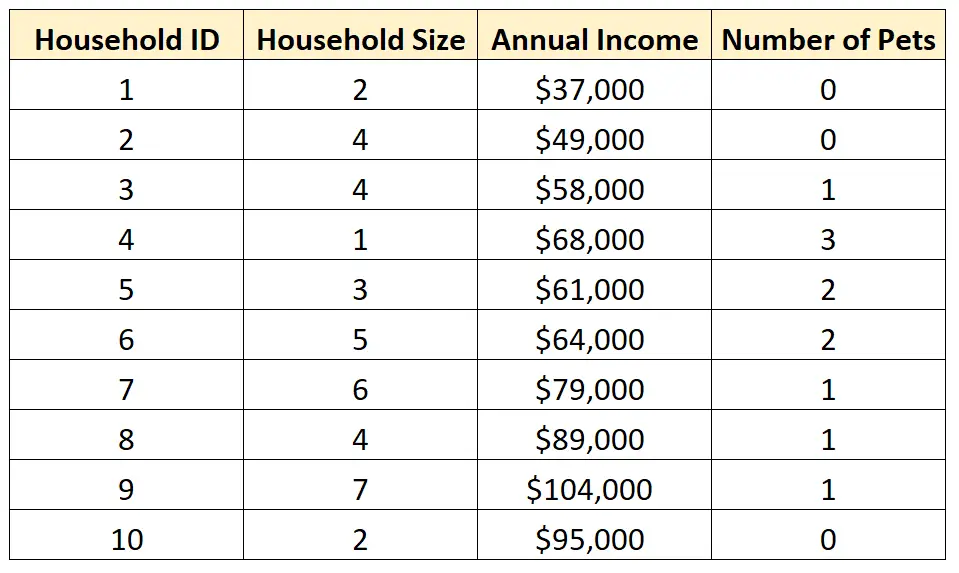
値の分布をよりよく理解するために、データセット内の個々の変数の 1 つに対して単変量分析を実行することを選択する場合があります。
たとえば、変数世帯規模に対して単変量分析を実行することを選択できます。
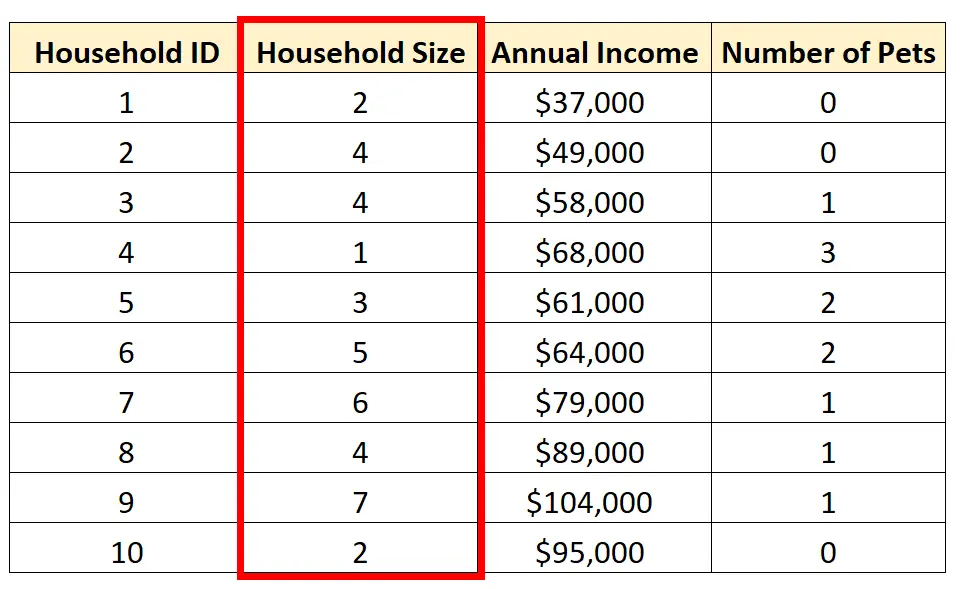
一変量解析を実行するには、次の 3 つの一般的な方法があります。
1. 概要統計
単変量分析を実行する最も一般的な方法は、要約統計量を使用して変数を記述することです。
要約統計量には一般的に 2 つのタイプがあります。
- 中心傾向の測定:これらの数値は、データセットの中心がどこにあるかを示します。例には、平均値と中央値が含まれます。
- 分散測定:これらの数値は、データセット内の値の分布を表します。例には、間隔、四分位範囲、標準偏差、分散などがあります。
2. 度数分布
単変量解析を実行するもう 1 つの方法は、データセット内に異なる値がどのくらいの頻度で現れるかを記述する頻度分布を作成することです。
3. グラフィックス
単変量分析を実行する別の方法は、グラフを作成して特定の変数の値の分布を視覚化することです。
一般的な例は次のとおりです。
- 箱ひげ図
- ヒストグラム
- 密度曲線
- カマンベール
次の例は、前述のデータセットの世帯人数変数を使用して、各タイプの一変量分析を実行する方法を示しています。

概要統計
世帯人数の中心的な傾向を示す以下の尺度を計算できます。
- アベレージ(平均値): 3.8
- 中央値(平均値): 4
これらの価値観は、「中心的な」価値観がどこにあるかについてのアイデアを与えてくれます。
次の分散尺度を計算することもできます。
- 範囲 (最大値と最小値の差): 6
- 四分位スケール (値の中央 50% の分布): 2.5
- 標準偏差 (スプレッドの平均尺度): 1.87
これらの値は、この変数の値の分布のアイデアを与えてくれます。
頻度分布
異なる値がどのくらいの頻度で発生するかを要約する次の度数分布表を作成することもできます。
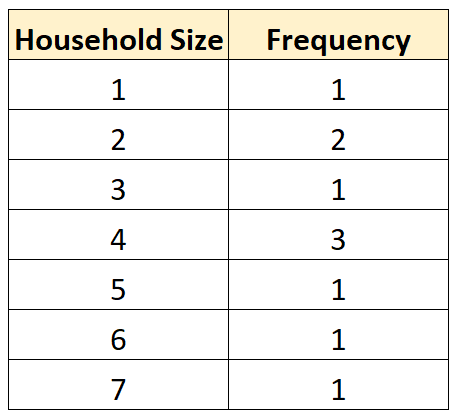
これにより、最も一般的な世帯人数は4 人であることがすぐにわかります。
リソース:この度数計算ツールを使用すると、任意の変数の度数分布を自動的に生成できます。
グラフィックス
次のグラフを作成すると、世帯人数の値の分布を視覚化できます。
1.箱ひげ図
箱ひげ図は、データセットの 5 桁の要約を示すグラフです。
5 つの数字の要約には次のものが含まれます。
- 最小値
- 最初の四分位
- 中央値
- 第 3 四分位
- 最大値
世帯規模変数の箱ひげ図は次のようになります。
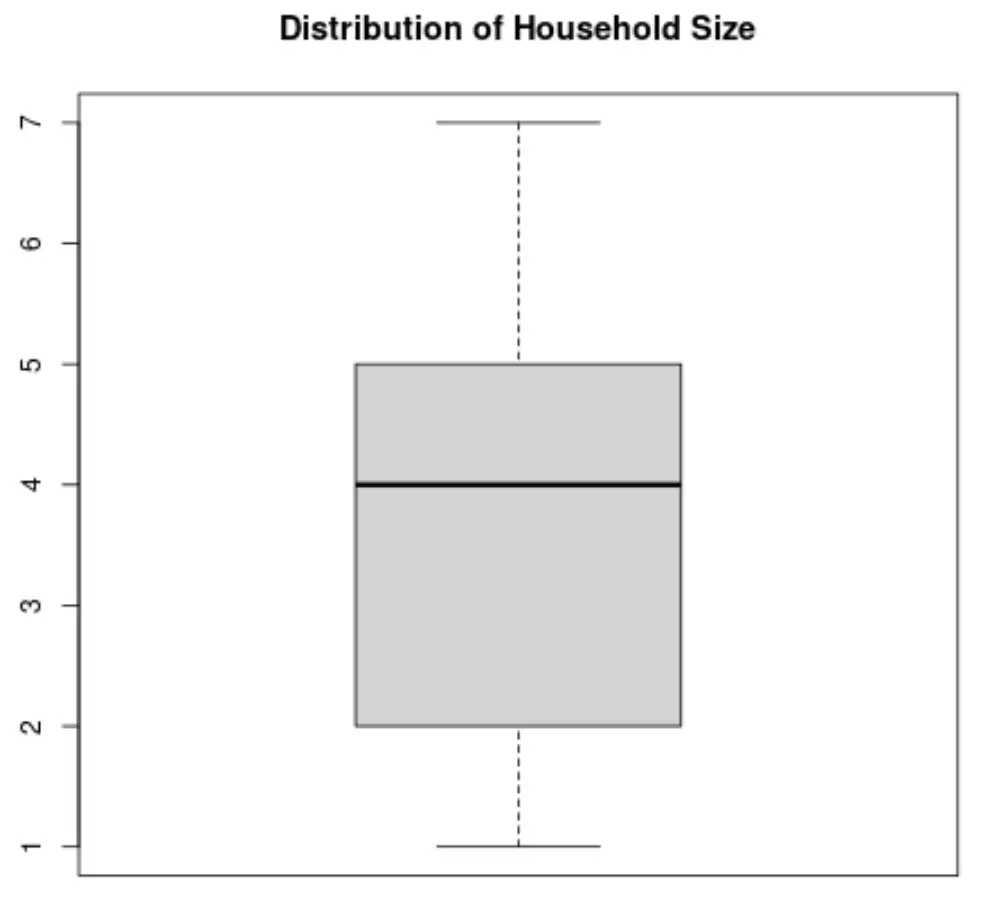
リソース:この箱ひげ図ジェネレーターを使用すると、任意の変数の箱ひげ図を自動的に作成できます。
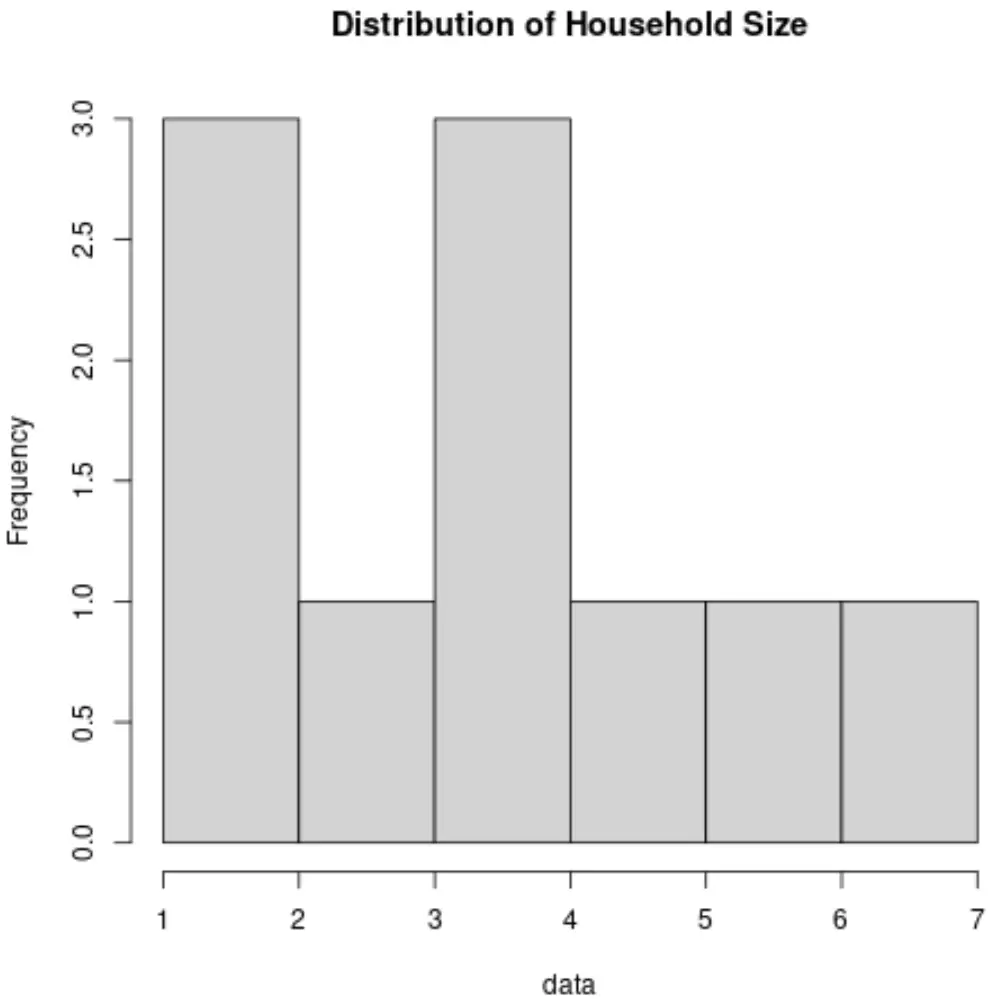
2. ヒストグラム
ヒストグラムは、縦棒を使用して度数を表示するグラフの一種です。このタイプのグラフは、データ セット内の値の分布を視覚化するのに便利な方法です。
世帯規模変数のヒストグラムは次のようになります。
3. 密度曲線
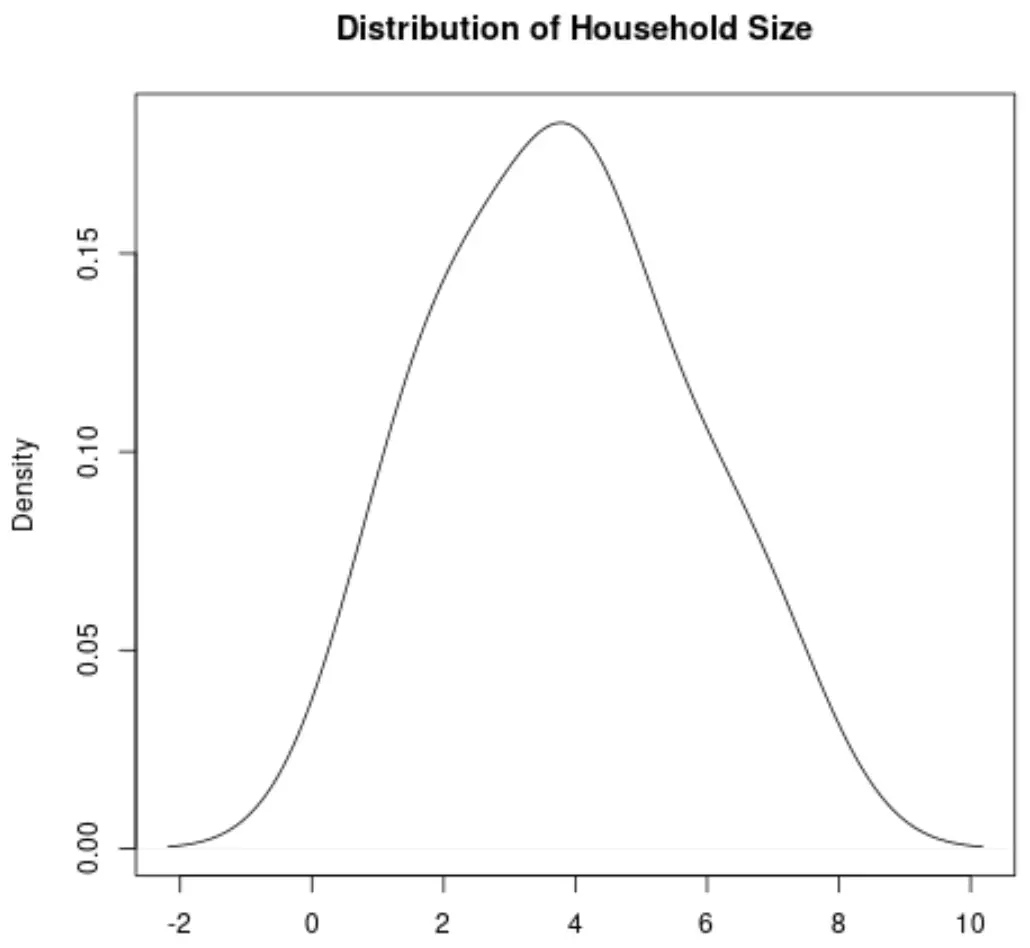
密度曲線は、一連のデータ内の値の分布を表すグラフ上の曲線です。
これは、分布に頻出値の1 つ以上の「ピーク」があるかどうか、 分布が左または右に偏っているかどうかなど、分布の「形状」を視覚化するのに特に役立ちます。
世帯規模変数の密度曲線は次のようになります。
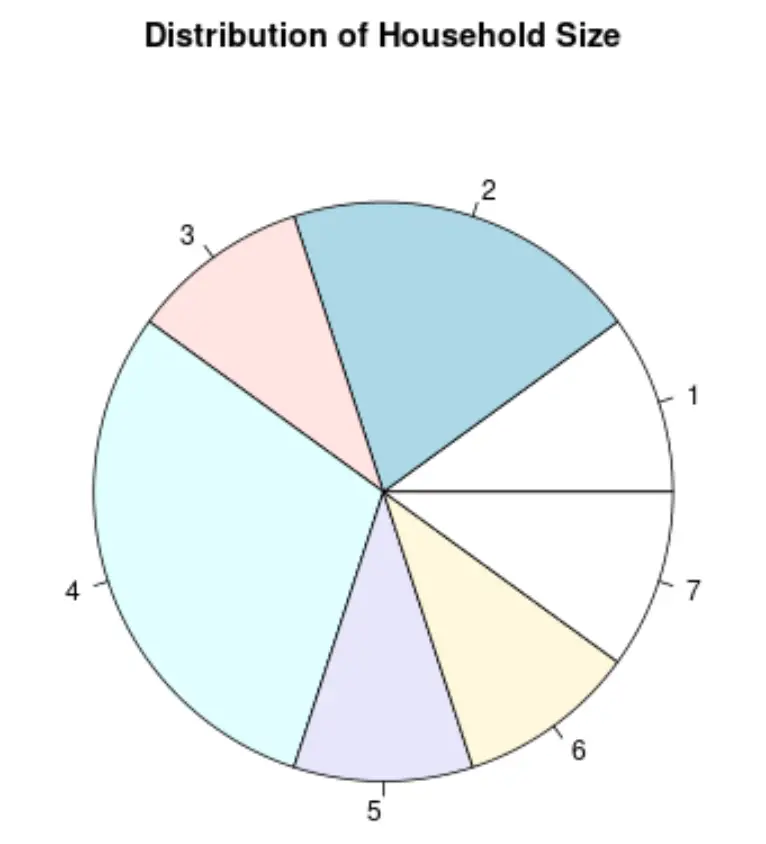
4. 円グラフ
円グラフは円グラフの一種であり、スライスを使用して全体の割合を表します。
世帯人数変数の円グラフは次のようになります。
データの種類によっては、値の分布を視覚化するために、これらのグラフの 1 つが他のグラフよりも役立つ場合があります。